数值法求解最优控制问题(四)——伪谱法
写在前面
数值法求解最优控制问题(二)——打靶法介绍了两种不同配点思路的直接法,一种是打靶法,一种是配点法,本篇文章介绍配点法。
配点法中又包含
- 欧拉法;
- Runge-Kutta 法;
- Hermit-Simpson 法;
- 伪谱法(pseudospectral method)。
伪谱法因其计算效率和计算精度上的优势、良好的收敛性以及较低的初值敏感度在最优控制领域求解算法中倍受关注。
整个最优控制中直接法的分类可见下图。

在这里主要介绍伪谱法。
伪谱法
伪谱法与一般配点法的区别在于,它利用全局多项式为基函数,在一系列离散点上对控制变量和状态变量进行插值近似,用 Guass 积分在离散点上实现微分代数方程的配置。
目前伪谱法常采用的配点有四类,分别为:
- Chebyshev-Gauss-Lobatto(CGL)点;
- Legendre-Gauss-Lobatto(LGL)点;
- Legendre-Gauss(LG)点;
- Legendre-Gauss-Radau(LGR)点。
这些配点是 Legendre 多项式或者 Legendre 多项式与其导数线性组合的根。
- 采用 CGL 点的称为 Chebyshev 伪谱法(CPM)。
- 采用 LGL 点的称为 Lobatto 伪谱法(LPM),也称为 Legendre 伪谱法;
- 采用 LG 点的称为 Gauss 伪谱法(GPM);
- 采用 LGR 点的称为 Radau 伪谱法(RPM)。
因 RPM 满足协态映射定理,且近似精度、收敛速度较其他配点法更优,本文着重介绍 RPM 法。
首先给出原理公式,随后再给出四类伪谱法的对比,从原理上解释四类伪谱法的优劣。
RPM 的原理
时域变换
将时间区间 $t \in [t_0,t_f]$ 转换到 $\tau \in [-1,1)$ 或 $\tau \in (-1,1]$ 上,转换公式为:
\[\begin{aligned} \tau &= \frac{2t-t_f-t_0}{t_f-t_0}, \\ t &= \frac{t_f-t_0}{2}\tau + \frac{t_f+t_0}{2}. \end{aligned}\]状态变量和控制变量的近似
RPM 选取$P_{n-1}(\tau) + P_n(\tau)$ 的零点,即 $n$ 阶 LGR 点 $\tau_n \ (n=1,2,\dots,N)$,以及 $\tau_0=-1$ 为节点,以 Lagrange 插值多项式为基函数近似状态变量和控制变量,为:
\[\begin{aligned} x(\tau) &\approx X(\tau) = \sum_{i=0}^N L_i(\tau)X(\tau_i), \\ u(\tau) &\approx U(\tau) = \sum_{k=1}^N \widetilde{L}_k(\tau) U(\tau_k), \end{aligned}\]注:请注意上面两式的起始点,一个是 $i=0$ ,一个是 $k=1$ 。
式中,$P_n(\tau)$ 为 $n$ 阶 Lengdre 多项式,表达式为:
\[P_n(x) = \sum_{m=0}^M (-1)^m \frac{(2n-2m)!}{2^n m! (n-m)! (n-2m)!} x^{n-2m},\]式中,
\[M = \left \{\begin{aligned} &\frac{n}{2}, &\quad 当\ n\ 为偶数时 \\ &\frac{n-1}{2}, &\quad 当\ n\ 为奇数时 \end{aligned} \right.\]Legendre 多项式的 Rodrigues 表达式为:
\[P_n(x) = \frac{1}{2^n n!} \frac{d^n}{x^n} (x^2-1)^n,\]Lagrange 插值多项式的数学描述为:
\[L_i(\tau) = \prod_{j = 0,j \ne i}^N \frac{\tau - \tau_j}{\tau_i - \tau_j}, \quad i = 1,2,\dots,N,\]式中,
\[L_i(\tau_j) = \left \{\begin{matrix} 1, \quad i = j, \\ 0, \quad i \ne j, \end{matrix} \right.\]Lagrange 插值多项式的插值误差为:
\[E_N(\tau) = \frac{(\tau-\tau_1) \cdots (\tau-\tau_N)}{N!} L^N(\zeta),\]式中,$L^N(\zeta)$ 为 $L_i(\tau)$ 的 $N$ 阶导数;$\zeta$ 是 $[t_0,t_f]$ 中的某个数, $N$ 越大,收敛速度越快。
微分方程约束转化为代数约束
对近似状态变量函数求导,得到状态变量导数,为:
\[\dot x(\tau_k) \approx \dot X(\tau_k) = \sum_{i=0}^N \dot{L}_i(\tau_k) X(\tau_i) = \sum_{i=0}^N D_{ki}X(\tau_i), \quad k = 1,2,\dots,K,\]式中,$D_{ki}$ 为微分矩阵(Differential Matrix),表达式为:
\[D_{ki} = \dot L_i(\tau_k) = \left \{ \begin{aligned} &\frac{\dot g(\tau_k)}{(\tau_k-\tau_i)\dot g(\tau_i)}, & (k \ne i),\\ &\frac{\ddot g(\tau_k)}{2\dot g(\tau_i)}, & (k = i), \end{aligned} \right.\]式中,
\[g(\tau_i) = (1+\tau_i)[P_N(\tau_i)-P_{N-1}(\tau_i)], \quad i = 0,1,\dots,N,\]最终,微分方程约束转化为代数约束,为:
\[F_k \equiv \sum_{i=0}^N D_{ki} X(\tau_i) - \frac{t_f-t_0}{2} f(X(\tau_i),U(\tau_i)) = 0, \quad k = 1,2,\dots,N.\]目标函数的近似
目标函数的形式已在数值法求解最优控制问题(〇)——定义给出,此处不再赘述,直接将目标函数中的积分项用 Gauss 积分近似,表达式为:
\[J \approx \Phi(x)(\mathbf{x}(t_0),t_0,\mathbf{x}(t_f),t_f) + \frac{t_f-t_f}{2}\sum_{k=1}^N w_k g(X(\tau_k),U(\tau_k),\tau_k;t_0,t_f),\]式中,
\[w_k = \int_{-1}^1 L_k(\tau) \text{d}t.\]约束条件的近似
通过前面的离散过程,RPM 已将连续最优控制问题转化为 NLP ,设计变量包括状态变量 $(X_0,X_1,\dots,X_N)$、控制变量 $(U_1,U_2,\dots,U_N)$、初始时刻 $t_0$ 和终端时刻 $t_f$。
约束条件包括微分方程约束,表达式为:
\[(F_1,F_2,\dots,F_N) = 0,\]边界条件约束,表达式为:
\[\phi(X(\tau_0),X(\tau_N)) = 0,\]和路径约束,表达式为:
\[\mathbf{C}(X(\tau_k),U(\tau_k),\tau_k;t_0,t_f) \le 0, \quad k=1,2,\dots,N.\]各伪谱法特点
下面从近似精度、收敛速度、计算效率以及是否满足协态映射原理四个方面说明 LPM、GPM 和 RPM 的特点。
补充知识
协态映射原理(Costate Mapping Principle,CMP):即说明伪谱法转换得到的非线性规划(NonLinear Programming,NLP)问题的Karush-Kuhn-Tucker(KKT)条件与原连续时间最优控制问题的一阶必要条件的离散形式是否具有一致性。如果一致,则表示保证原连续时间最优控制问题的协态可以由NLP问题的Lagrange乘子估计得到,从而保证了从NLP问题得到的最优解是原连续时间最优控制问题的最优解。
- 近似精度:GPM 和 RPM 在控制变量、状态变量和协态变量的近似精度优于 LPM。
- 收敛速度:LPM、GPM 和 RPM 的解均成指数规律收敛,但GPM 和 RPM 在收敛速度上优于LPM。
- 计算效率:对于相同规模问题的求解,LPM、GPM 和 RPM 耗时相差不大。
- 协态映射原理:GPM 和 RPM 是满足协态映射原理,LPM 不满足协态映射原理。
- 其他:与 GPM 相比,RPM 能够直接从相应的 NLP 问题的最优解中得到初始点的控制变量,而 GPM 不行,RPM 的这一性质使得在hp-伪谱法中采用 RPM 时,段与段的连续性方程可以略去,从而减少了约束方程的个数,使得 RPM 的实现比 GPM 简单。
各伪谱配点的分布特点
配点的分布是不同配点算法的重要区别。
一般配点法将时间区间等距划分,即配点分布是均匀的。但这样的配点存在缺点,会出现龙格现象(Runge phenomenon),如下图所示。

注:$y(\tau)=1/(1+50\tau^2) \quad \tau \in [-1,+1]$,$Y(\tau)$ 为高阶次插值函数。
可以看见曲线两端波动极大、振荡明显,导致插值区间的边缘部分误差极大。
伪谱法将时间区间 $t \in [t_0,t_f]$ 转换到 $\tau \in [-1,1]$ 后,采用 LG 、 LGR 和 LGL 等非均匀分布的配点将连续区间 $[-1,1]$ 离散化,这样的话就不会产生龙格现象了。
需要注意的是:
- LG 点是 Legendre 多项式 $P_n(\tau)$ 的零点;
- LGR 点是 Legendre 多项式 $P_{n-1}(\tau) + P_n(\tau)$ 的零点;
- LGL 点是 Legendre 多项式 $P_{n-1}(\tau)$ 的驻点(导数为零的点)。
Legendre 多项式零点分布特点为中间稀疏、两边稠密。具体地,
- LG 点在 $[-1,1]$ 上不包含 $\tau=-1$ 和 $\tau=1$ 两个端点;
- LGR 点在 $[-1,1]$ 上包含一个端点,即包含 $\tau=-1$ 或 $\tau=1$;
- LGL 点在 $[-1,1]$ 上包含 $\tau=-1$ 和 $\tau=1$ 两个端点;
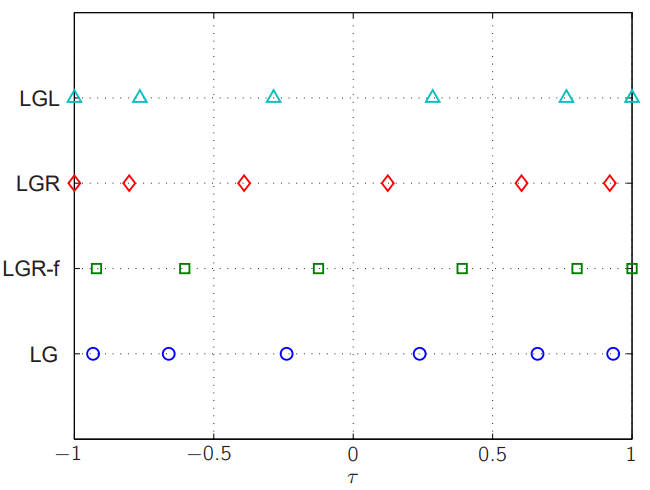
离散点数为 6 点时,LG、LGR、LGL 点的分布如下图所示。
LGL 点不满足协态映射定理的原因
为什么LGL点不满足协态映射定理呢?因为LGL点包含 $\tau=-1$ 和 $\tau=1$ 两个边界点。而在边界点处是不满足动力学离散形式的,无法准确估计协态变量,所以无法将最优控制问题等价地转换为 NLP 问题。
至于为什么在边界点不满足动力学形式,Divya Gang 在论文1 指出:
原文是:
It is noted, however, that at the boundary points, the discrete equivalents of continuous boundary conditions (3–48) and (3–49) are coupled in the discrete costate dynamics in (3–98) and (3–99), respectively.
在这里列出来式(3–48)、(3–49)、(3–98)和(3–99)。
\[\boldsymbol{\lambda}(-1) = -\nabla_{y(-1)}(\Phi-\langle \psi,\phi \rangle) \tag{3-48}\] \[\boldsymbol{\lambda}(+1) = \nabla_{y(+1)}(\Phi-\langle \psi,\phi \rangle) \tag{3-49}\] \[\begin{aligned} \mathbf D_1^{\dagger } \boldsymbol{\widetilde{\lambda}} &=-\frac{t_f-t_0}{2} \nabla_{Y_1}(g_1+\langle \boldsymbol{\widetilde{\lambda}}_1, \mathbf{f}_1 \rangle-\langle \widetilde{\gamma}_1,\mathbf{C}_1 \rangle) \\ & - \frac{1}{w_1} \left ( \boldsymbol{\widetilde{\lambda}}_1 + \nabla_{Y_1}(\Phi-\langle \widetilde{\psi},\phi\rangle) \right ), \end{aligned} \tag{3-98}\] \[\begin{aligned} \mathbf D_N^{\dagger } \boldsymbol{\widetilde{\lambda}} &=-\frac{t_f-t_0}{2} \nabla_{Y_N}(g_N+\langle \boldsymbol{\widetilde{\lambda}}_N, \mathbf{f}_N \rangle-\langle \widetilde{\gamma}_N,\mathbf{C}_N \rangle) \\ & - \frac{1}{w_N} \left ( \boldsymbol{\widetilde{\lambda}}_N + \nabla_{Y_N}(\Phi-\langle \widetilde{\psi},\phi\rangle) \right ). \end{aligned} \tag{3-99}\]因为在一个区间内LGL点的末端点与下个区间的初始点是一个点,但是计算公式又不是一样的,导致产生耦合现象,所以在这一点上估计协态变量的精度不准确,自然也不满足协态映射定理了。而LGR点和LG在区间内不会把初末端点值全部占满,所以不会出现耦合现象,自然满足协态映射定理了。
LGL、LG、LGR 三种配点方式得到的配点见下图。
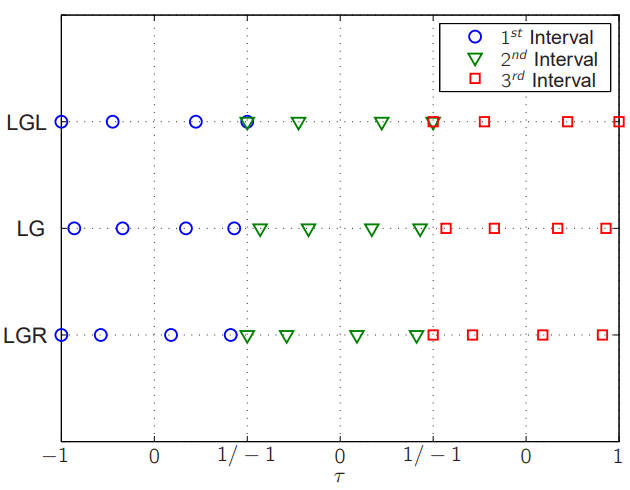
从上面的图也可以看出,LG 和 LGR 的配点满足协态映射定理。
上图没有显示 CGL 点的情况,通过计算公式并编写 matlab 代码,可以得到:CGL 点同样包含 $\tau=-1$ 和 $\tau=1$ 两个端点,所以 CGL 的配点同样不满足协态映射定理。
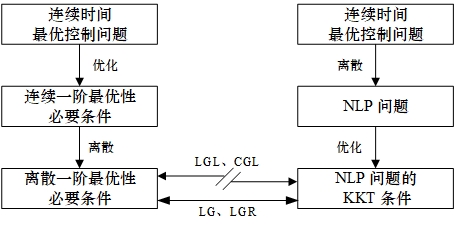
下图可以总结 LG、LGR、LGL 和 CGL 四种配点方式满足协态映射定理的情况。
算法步骤
- 确定最优控制问题的离散点数、起止时间、子时间区间段数、状态变量初值、控制变量初值;
- 根据不同配点方法求取配点;
- 正确编写约束条件,这一步很重要,关系到伪谱法是否能够成功求解最优控制问题;
- 将目标函数转化为离散形式;
- 调用 matlab 的
fmincon()求解该 NLP 问题。
算例
该算例选自《最优化与最优控制》第2版第257页例13.1。
设由状态方程及初始条件 $\dot x = -x^2+u$ ,$x_0=10$ ,性能指标 $J(u)=0.5\int_{0}^{1}(x^2+u^2)\text{d}t$ ,求解最优控制使 $J$ 为极小。
代码
这里给出伪谱法的完整代码,里面包含了 LGR、LGL 和 CGL 的配点方法。
%--------------------------------------------------------------------------
% Method_Pseudospectral.m
% Attempt to solve the Bryson-Denham problem using a pseudospectral method
% (namely LGL nodes and Gaussian quadrature)
%--------------------------------------------------------------------------
%
%--------------------------------------------------------------------------
% Primary Contributor: Daniel R. Herber, Graduate Student, University of
% Illinois at Urbana-Champaign
% https://github.com/danielrherber/optimal-control-direct-method-examples
%--------------------------------------------------------------------------
%--------------------------------------------------------------------------
% 说明:应用伪谱法求解无约束最优控制问题
% 例子:《最优化与最优控制》 pp. 257 例13.1
% 类型:无控制约束的最优控制问题
% 时间:2022/07/07
%--------------------------------------------------------------------------
clear;clc;close all;
%% 01 初始参数设置
p.ns = 1; p.nu = 1; % 状态量个数和控制量个数
p.t0 = 0; p.tf = 1; % 初始时间和终止时间
p.x0 = 10; % 初始条件
p.nt = 20; % 配置点个数
% p.method = 'LGL'; % 选择配点方式:Legendre-Gauss-Lobatto(LGL)
% p.method = 'CGL'; % 或者 Chebyshev-Gauss-Lobatto(CGL)
p.method = 'LGR'; % 或者 Legendre-Gauss-Radau(LGR)
if strcmp(p.method,'LGL')
p.tau = LGL_nodes(p.nt-1); % 把时间区间离散到[-1,1]中
p.D = LGL_Dmatrix(p.tau); % 微分矩阵
p.w = LGL_weights(p.tau); % 配置点权重
elseif strcmp(p.method,'CGL')
p.tau = CGL_nodes(p.nt-1); % 把时间区间离散到[-1,1]中
p.D = CGL_Dmatrix(p.tau); % 微分矩阵
p.w = CGL_weights(p.tau); % 配置点权重
elseif strcmp(p.method,'LGR')
[p.tau,p.w] = LGR_nodes_and_weights(p.nt-1);
p.D = LGR_Dmatrix(p.tau); % 微分矩阵
end
% 将变量离散为 x = [x,u]
p.x_index = 1:p.nt;
p.u_index = p.nt+1:2*p.nt;
%% 02 求解算法
% 给[x;u]赋初值
y0 = zeros(p.nt*(p.ns+p.nu),1);
% 求解器设置
options = optimoptions(@fmincon,'display','iter','MaxFunEvals',1e5,'algorithm','sqp');
tic;
[y,fval] = fmincon(@(y) objective(y,p),y0,[],[],[],[],[],[],@(y) constraints(y,p),options);
toc;
% 得到求解结果
p.x = y(p.x_index); % 状态量
p.u = y(p.u_index); % 控制量
p.t = tau2t(p); % 把时间变量从 tau 转化为 t
%% 03 画图
window_width = 500;
window_height = 416;
% 状态量
k = 1;
figure('color',[1 1 1],'position',[300+k*window_width,300,window_width,window_height]);
plot(p.t, p.x, 'o-', 'LineWidth',1.5);hold on;
plot(p.t, p.u, 'x-', 'LineWidth',1.5);
xlabel('Time');
ylabel('State & control');
set(gca,'FontSize',15,...
'FontName','Times New Roman',...
'LineWidth',1.5);
legend('$x(t)$','$u(t)$',...
'Location','Northeast',...
'FontSize',10,...
'interpreter','latex');
% 保存数据
% .\ 下一级文件夹
% ..\ 上一级文件夹
% save(['..\','pseudospectral_method.mat']);
%% 04 子函数部分
% 目标函数
function J = objective(y,p)
% 得到状态量和控制量
x = y(p.x_index);
u = y(p.u_index);
L = u.^2 + x.^2; % 积分项
J = (p.tf-p.t0)/2 * dot(p.w,L)/2; % 计算目标函数
end
% 约束函数
function [c,ceq] = constraints(y,p)
% 得到状态量和控制量
x = y(p.x_index);
u = y(p.u_index);
% 状态方程约束
Y = x; F = (p.tf-p.t0)/2*(-x.^2+u);
% 初始状态约束
ceq1 = x(1) - p.x0;
ceq2 = p.D*Y - F;
% 输出约束条件
ceq = [ceq1;ceq2(:)];
c = [];
end
% 把 tau 转换为 t
function t = tau2t(p)
% 按照《天基对地打击武器轨道规划与制导技术》2013 pp.79 式(4.25)编写如下代码
t = (p.tf-p.t0)*p.tau/2+(p.tf-p.t0)/2;
end
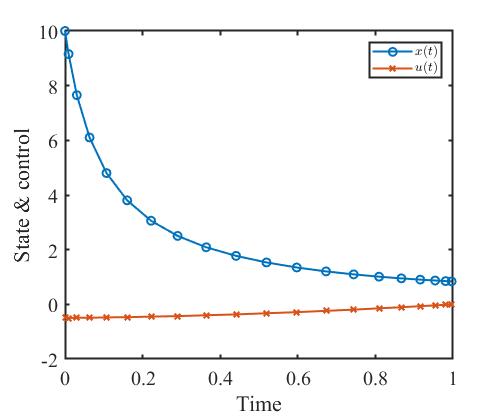
结果
状态量和控制量的变化曲线如下。
对比
下面对比 RPM、LPM、CPM、单次打靶法和多重打靶法在离散点数为 20 点、30 点、40 点和 50点的计算时间。
笔记本电脑参数为:
- 型号:联想 Thinkpad T490
- 处理器:Intel(R) Core(TM) i5-8265U CPU @ 1.60GHz x86
- 内存: DD4R 2400 MHz 8GB + DD4R 2667 MHz 8GB
- 电源模式:平衡模式
仿真结果如下。

在图中标记时间显得比较凌乱,所以在表格中给出上述五种算法在不同离散点数下的计算时间,表格如下。
| RPM | LPM | CPM | 单次打靶法 | 多重打靶法 | |
|---|---|---|---|---|---|
| 20 点 | 0.2255 | 0.2535 | 0.2861 | 0.2116 | 0.0875 |
| 30 点 | 0.3905 | 0.5488 | 0.5888 | 0.4328 | 0.1659 |
| 40 点 | 0.5183 | 0.9558 | 1.0617 | 0.7834 | 0.2385 |
| 50 点 | 1.1985 | 1.3719 | 1.4135 | 1.5981 | 0.3731 |
从上面图表可知,多重打靶法的计算速度是最快的,RPM次之,随后是单次打靶法(不过离散点数为 50 点时计算时间陡增),最后是 LPM 和 CPM。
总结
伪谱法到这里已经介绍完毕,从(〇)到(四),我首先给出最优控制问题的定义,再分别介绍梯度法、单次打靶法、多重打靶法和伪谱法的原理,并针对一个最优控制问题算例编写 matlab 代码。
通过写这些技术博客,我对上面的方法有进一步的认识。把自己的代码分享出来呢,也是因为自己在学习过程中苦于找代码的过程,没有代码就没有实践,自然学习效果不好。所以想把代码开源,希望可能帮助到从事这个领域的朋友。
-
Garg D. Advances in global pseudospectral methods for optimal control[D]. University of Florida, pp.75, 2011. ↩