写在前面

上一篇文章里（数值法求解最优控制问题（一）——梯度法），介绍了使用梯度法求解最优控制问题的原理，并且给出了matlab代码。梯度法具有代码编写简单的优点，但其算法效果受步长的影响较大¹。

此外，梯度法需要先依据极大值原理推导一阶最优必要性条件，再通过梯度法求解哈密顿函数值 $H$ ，并且沿着负梯度方向更新控制量 $u$ ，直至满足终止条件。

显然可见，该方法仍然需要进行手动推导，才能进行后面的算法流程。那么有没有连一阶最优性必要条件都不用推导的方法呢？

有的。

叫做直接法。

直接法采用配点思想对原最优控制问题进行离散，离散后的最优控制问题便转化为非线性规划问题（NonLinear Programming，NLP），再选用数值优化方法求解NLP问题，获得原最优控制问题的最优解。

依据配点思路的不同，可以分为：

• 打靶法，特点为仅离散控制变量；
• 配点法，特点为同时离散状态变量和控制变量。

本篇文章先介绍打靶法中的单步直接打靶法（Direct Single Step Shooting Method，DSSSM。后文简称打靶法）。

打靶法

这里先介绍打靶法的基本原理，并按照数值法求解最优控制问题（一）——梯度法的算例，给出matlab代码。

打靶法在时域上离散控制变量将其转化为NLP问题进行求解，该方法以离散时间点上的控制变量为设计变量，时间节点之间的控制变量可通过插值得到。

离散过程的数学描述为：

式中，$N$ 为离散时间区间段数，$m$ 为控制量的维度。

在数值法求解最优控制问题（〇）——定义给出了最优控制问题的四大组成部分，即

• 性能指标；
• 控制系统微分方程约束；
• 边界约束；
• 路径约束。

下面给出四部分的转化过程。

性能指标转化过程

对于性能指标

将其分为Mayer型和Lagrange型性能指标讨论。

对于Mayer型性能指标

根据 $\boldsymbol{x}(t)=g(u(t),t)$ ，可将其转化为

对于Lagrange型性能指标

根据辛普森积分，可将其转化为

综上所述，性能指标可转化为

控制系统微分方程约束转化过程

控制系统微分方程约束为：

离散后的控制变量作为设计变量，可认为是已知量，因此可根据上述控制系统微分方程约束求解处状态变量 $\boldsymbol{x}(t)$，即

求解得到的 $\boldsymbol{x}(t)$ 是关于 $(\boldsymbol{u}(t),t)$ 的函数。

边界约束转化过程

边界约束为：

因为 $\boldsymbol{x}(t_0), \boldsymbol{x}(t_f)$ 都是关于 $(\boldsymbol{u}(t),t)$ 的函数，代入上式替换后可表示为：

注：$C$ 为constraints的缩写，代表约束；$B$ 为boundary的缩写，代表边界。

路径约束转化过程

路径约束为：

根据 $\boldsymbol{x}(t)=g(u(t),t)$ ，可将其转化为

此时，已把最优控制问题转化为NLP。K.L.Teo²指出，当离散点趋向无穷多时，该NLP问题的解与最优控制问题的解等价。

算法步骤

1. 确定最优控制问题的离散点数、起止时间、状态变量初值、控制变量初值；
2. 计算控制变量数量和约束条件数量：
   • 控制变量数量 = 控制变量维度 * 离散点数，
   • 约束条件数量 = 状态变量维度 * 离散点数 + 边界条件数量 + 路径约束数量 * 离散点数，
   • 若终端时间不固定，则需将设计变量个数加 1。
3. 将目标函数转化为离散形式；
4. 调用 matlab 的 fmincon() 求解该 NLP 问题。

算例

该算例选自《最优化与最优控制》第2版第257页例13.1。

设由状态方程及初始条件 $\dot x = -x^2+u$ ，$x_0=10$ ，性能指标 $J(u)=0.5\int_{0}^{1}(x^2+u^2)\text{d}t$ ，求解最优控制使 $J$ 为极小。

代码

打靶法原理十分简单，在这里直接给出完整代码，可以从代码中学习打靶法的原理。

%--------------------------------------------------------------------------
% 说明：应用直接打靶法求解无约束最优控制问题
% 例子：《最优化与最优控制》 pp. 257 例13.1 
% 类型：无控制约束的最优控制问题
% 时间：2022/07/01
%--------------------------------------------------------------------------
clear;clc;close all;

%% 01 初始参数设置
p.ns = 1; p.nu = 1;                     % 状态量个数和控制量个数
p.t0 = 0; p.tf = 1;                     % 初始时间和终止时间
p.x0 = 10;                              % 初始条件

% 直接打靶法参数设置
p.nt = 20;                              % 打靶点参数设置
p.t = linspace(p.t0,p.tf,p.nt)';        % 时间区间

% 将控制量离散
p.u_index = 1:p.nt;

%% 02 求解算法
% 给控制量赋初值
p.u = -0.5*ones(p.nt,1);
u0 = p.u;              % 控制量的初值猜测

% 求解控制量
options = optimoptions(@fmincon,'display','iter','MaxFunEvals',1e5,'algorithm','sqp');
tic;
[u,fval,exitflag,output] = fmincon(@(u) objective(u,p),u0,[],[],[],[],[],[],[],options);
toc;
p.u = u;
time_record = toc;

% 再进行一次仿真得到数据
[~,Y] = ode45(@(t,y) derivative(t,y,p),p.t,p.x0);
p.x = Y(:,1);

%% 画图
k = 0;
window_width = 500;
window_height = 416;

% 状态量
fig.k = 0;
figure('color',[1 1 1],'position',[300+k*window_width,300,window_width,window_height]);
plot(p.t, p.x, 'x-', 'LineWidth',1.5);hold on;
plot(p.t, p.u, 'x-', 'LineWidth',1.5);
xlabel('Time');
ylabel('State & control');
set(gca,'FontSize',15,...
        'FontName','Times New Roman',...
        'LineWidth',1.5);
legend('$x(t)$','$u(t)$',...
        'Location','Northeast',...
        'FontSize',10,...
        'interpreter','latex');

% 保存数据
% .\ 下一级文件夹
% ..\ 上一级文件夹
% save(['..\','shooting_method.mat']);

%% 子函数部分
% 目标函数
function f = objective(u_obj,p)
    p.u = u_obj(p.u_index);
    [~,Y] = ode45(@(t,y) derivative(t,y,p),p.t,p.x0); % 仿真得到时序状态量
    x = Y;                          % 状态量
    u = u_obj(p.u_index);           % 控制量
    L = u.^2/2 + x.^2/2;            % 积分项
    f = trapz(p.t,L);               % 计算目标函数
end

% 状态方程
function dy = derivative(t,y,p)
    % 使用 interp1qr() 进行插值
%     u = interp1qr(p.t,p.u,t);
    % 使用 interp1q() 函数进行插值
    % 发现 interp1q() 的速度比 interp1() 快，和nterp1qr() 速度一样
    u = interp1q(p.t,p.u,t);
    % 使用 interp1() 函数进行插值
%     u = interp1(p.t,p.u,t);    
    dy = -y^2 + u;
end

结果

状态量和控制量的变化曲线如下。

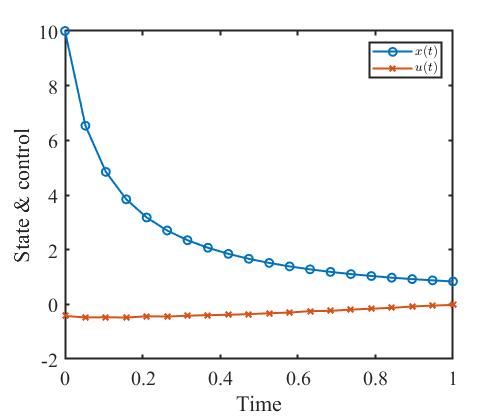
对比

不同插值函数对计算时长的影响

使用打靶法时，计算时长比梯度法慢。

我的笔记本电脑参数为：

• 型号：联想 Thinkpad T490
• 处理器：Intel(R) Core(TM) i5-8265U CPU @ 1.60GHz x86
• 内存： DD4R 2400 MHz 8GB + DD4R 2667 MHz 8GB
• 电源模式：平衡模式

在笔记本上运行代码，梯度法的计算时长为 0.1163 秒，打靶法的计算时长为 1.3632 秒。

打靶法的计算时长是梯度法的 11.7214 倍。

查看 matlab 的运行用时分析，了解到是插值函数 interp1() 占用了绝大部分用时。为了减少打靶法的计算时间，可以对 interp1() 进行优化，或选用消耗更少的插值函数。

matlab中有个 interp1q() 函数，但目前 mathwork 已不推荐使用该函数。不过用它进行插值的速度十分快，这个函数是一种快速一维插值方法，运行速度比 interp1() 更快，但因为提供的插值方式少，且代码编写年代久远，所以已经不推荐使用该函数。不过在本算例中还是可以继续发挥作用的。

关于为什么 interp1() 函数计算时间长的问题，MATLAB一维插值加快运行速度的方法给出了介绍。

interp1(Xvec,Vvec,xq,method) 对于 Xvec 在 xq 中的插值处理，是将 Xvec 从前至后排列好，再依次比较大小，最后定位到特定的时间区段内。

用伪代码来表示，即：

for i = 1:length(Xvec) - 1
    if xq < Xvec(i) && xq > Xvec(i+1)
        在 [Xvec(i), Xvec(i+1)] 区间内线性插值
    else
        继续比较大小，定位 xq 的位置，确定使用哪一段的 [Xvec(i), Xvec(i+1)] 区间
    end
end

在 mathwork 的 file exchange 里找到了另外一个插值函数 interp1qr() ，Quicker 1D linear interpolation: interp1qr。

作者在介绍里面说，

It runs at least 3x faster than ‘interp1q’ and 8x faster than ‘interp1’, and more than 10x faster as m=length(x) increases (see attached performance graph).

大意为 interp1qr() 的运行效率比 interp1q() 快3倍，比 interp1qr() 快10倍。

下面对比 interp1() 、interp1q() 和 interp1qr() 三个函数的打靶法计算时长。

仿真结果如下。

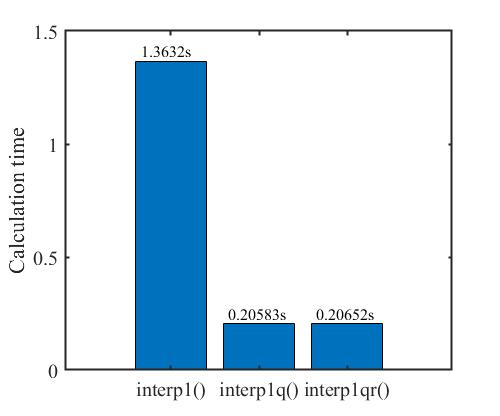
状态量和控制量的变化曲线基本一样，为避免累赘，这里不再放仿真图。

interp1q() 和 interp1qr() 的计算时长基本一致，没有如同作者说的 It runs at least 3x faster than ‘interp1q’ ，原因或许是算例问题比较简单，没有发挥出来 interp1qr() 的优势，在后面的学习过程中说不定会有新的体会和发现。interp1() 的计算时长最长，因为它在使用过程中进行了很多检查工作，但这些检查工作其实没有必要，写代码的时候已经检查过一遍了，出错几率低。调用次数少的时候，检查一下没有关系，但调用次数多了之后，每回都要检查，这无疑加重了计算机的负担；另外，interp1() 的插值方式存在缺陷，这又是导致计算时间长的原因。

通过这次对比仿真，可以得出结论，在使用较为简单的插值场景中，可以选用 interp1q() 和 interp1qr() 函数来降低计算消耗，减少计算时间。

不同离散点数对计算时长的影响

这里给出离散点数为20点、30点、40点、50点时的仿真结果。

不同离散点数对应的计算时长为：

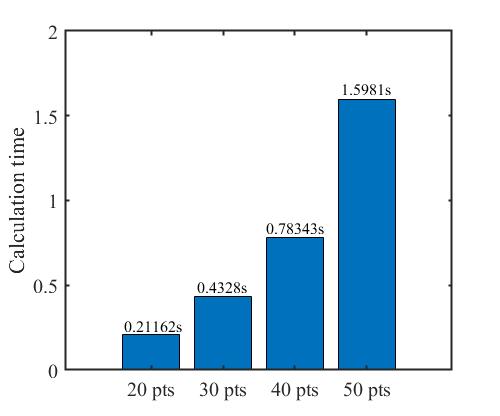
注：pts 为点数（points）之意。

不同离散点数对应的状态量变化曲线为：

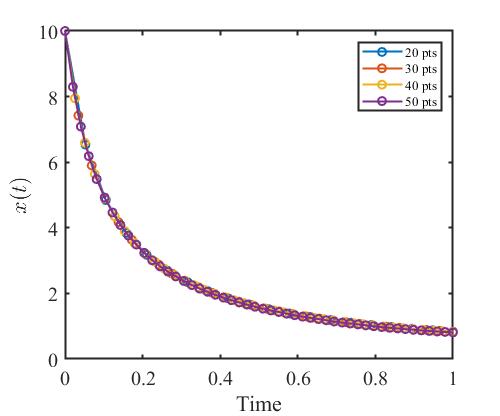
不同离散点数对应的控制量变化曲线为：

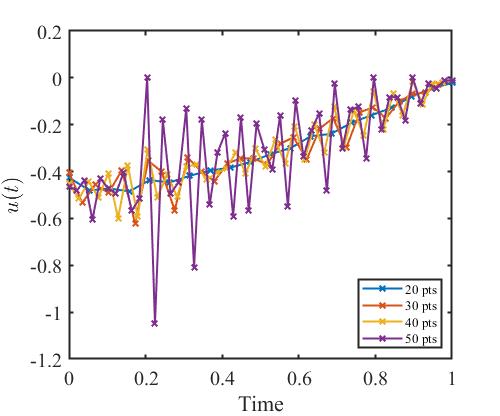
可以看出，离散点越多，计算时长越长。

不同离散点数对应的状态量没有区别。

但是离散点越多，控制量变化越大，点与点之间的连接线十分陡峭，这在现实中是不可用的。

对比仿真结果，可以发现，选择20个离散点已经具有很好的效果，再添加离散点数反而会让算法效果更差，计算时间更长，因此在打靶法中离散点数的选择是十分重要的。