数值法求解最优控制问题(一)——梯度法
写在前面
最优控制问题可以使用变分法来进行求解,当问题是有约束的最优控制问题时,可以采用极小值原理求解该最优控制问题。上述方法称为解析法。但是,一旦问题约束条件或目标函数复杂,使用解析法求解最优控制问题面临着极大困难,也有可能出现解析解难以求解的问题。
为此,研究者将目光转向了数值解法。 e 数值解法的本质就是代替了人用脑和手计算最优控制问题的过程,采用数值优化技术完成控制结果的求解。
下面介绍一种实现简单的数值解法,即梯度法(gradient method,GM)。
梯度法
梯度法的另一个名字是最速下降法(steepest descent method,SDM),基本思想是先根据Pontryagin极大值原理(后文简称极大值原理)推导一阶最优必要性条件,求取最优控制 $u^*$ 使得哈密顿函数 $H$ 最小。
算法流程是首先根据经验猜测一个初始控制量 $u^0$,再通过数值算法求出 $H^0$ 。随后根据求出的 $H^0$ 来修改 $u$ ,使得 $H$ 继续减小,直到趋近最小值停止。修改 $u$ 的目的就是为了让 $H$ 逐渐减少,修改方向为 $H$ 的“最陡下降”方向,即负梯度方向。这就是被称为梯度法的原因。
讨论一类控制不受约束的最优控制问题。
给定系统状态方程为
\[\boldsymbol{\dot x} = f(\boldsymbol{x},\boldsymbol{u},t), \tag{1}\]初始条件为
\[\boldsymbol x(t_0) = \boldsymbol{x}_0, \tag{2}\]性能指标为
\[J(\boldsymbol u) = \Phi(\boldsymbol x_T,T) + \int_{T}^{t_0}L(\boldsymbol x, \boldsymbol u, t), \tag{3}\]其中,$\Phi(\boldsymbol x_T,T)$ 被称为Mayer型性能指标(或称常值型性能指标),$\int_{T}^{t_0}L(\boldsymbol x, \boldsymbol u, t)$ 被称为Lagrange型性能指标,(或称积分型性能指标)。既有Mayer型,又有Lagrange型的性能指标 $(3)$ 被称为Bolza型性能指标(或称复合型性能指标)。
在这里,最优控制的目标就是寻找一个 $u^*$ 使得 $J$ 最小。
构造哈密顿函数为
\[H(t,\boldsymbol{x},\boldsymbol{u},\boldsymbol{\lambda})=L(t,\boldsymbol{x},\boldsymbol{u}) + \boldsymbol{\lambda}^{\rm T}(t)f(\boldsymbol{x},\boldsymbol{u},t), \tag{4}\]省去推导步骤1,得到泛函 $J^k(\boldsymbol{u})$ 在 $\boldsymbol{u}^k(t)$ 处的梯度,即
\[\nabla J(\boldsymbol{u^k}) = \frac{\partial H}{\partial \boldsymbol{u^k}}. \tag{5}\]根据极大值原理,在 $J(\boldsymbol{u})$ 的极小点处满足下式,为
\[\boldsymbol{\dot \lambda} = -\frac{\partial H}{\partial \boldsymbol{x}}, \quad \boldsymbol{\lambda}(T) = \frac{\partial K}{\partial \boldsymbol{x}_T}, \tag{6}\] \[\frac{\partial H}{\partial \boldsymbol{u}} = 0. \tag{7}\]至此,求解最优控制问题变为联立求解方程 $(1)$ 、$(2)$、$(5)$、$(6)$ 的两点边值问题(two-point boundary value problem,TPBVP)。
算法步骤
下面给出梯度法的步骤。
- 根据系统状态方程和目标函数建立哈密顿函数 $(4)$ 和伴随方程 $(5)$。
- 猜测第 0 步的控制量 $\boldsymbol u^0(t)$ ,$k=0$ 。
- 把 $\boldsymbol u^k(t)$ (在算法开始时,$k=0$)代入 $(1)$ 和 $(2)$ 中,进行正向积分,得到 $\boldsymbol{x}^k(t)$。
- 根据伴随方程和末值条件 $(5)$ 反向积分,得到 $\boldsymbol{\lambda}^k(t)$。
- 把 $\boldsymbol u^k(t)$ 、 $\boldsymbol{x}^k(t)$ 和 $\boldsymbol{\lambda}^k(t)$ 代入到 $(3)$ 求解性能指标 $J(\boldsymbol{u^k})$ 以及梯度 $\nabla J(\boldsymbol{u^k}) = \partial H / \partial \boldsymbol{u^k}$。
- 确定步长参数 $K^k$ 以及修改量 $\Delta u^{k}(t) = -K^k \nabla J(\boldsymbol{u^k}) k$。
- 更新控制量 $\boldsymbol{u}^{k+1}(t) = \boldsymbol{u}^{k}(t) + \Delta u^{k}(t)$。
- 更新下一步 $k=k+1$ ,判断 $\bigtriangledown J(\boldsymbol{u^k})$ 小于设定值 $\varepsilon$。若满足要求,则退出循环;否则,重复第3步至第7步的迭代过程,直至满足终止条件。
下面会先给一个算例,再根据算例详细解释梯度法步骤,随后给出代码。
算例
该算例选自《最优化与最优控制》第2版第257页例13.1。
设由状态方程及初始条件 $\dot x = -x^2+u$ ,$x_0=10$ ,性能指标 $J(u)=0.5\int_{0}^{1}(x^2+u^2)\text{d}t$ ,求解最优控制使 $J$ 为极小。
详细解释
下面根据算例对梯度法步骤进行详细解释。
1)首先需要推导出哈密顿函数 $(4)$ 、伴随方程 $(5)$ 和梯度 $(6)$ 的表达式,为
\[\begin{aligned} &H = 0.5*(x^2+u^2) - \lambda (x^2+u), \\ &\boldsymbol{\dot \lambda} = -\frac{\partial H}{\partial x} = -x + 2\lambda x, \quad \lambda(1) = 1, \\ &\nabla J = \frac{\partial H}{\partial u} = u+\lambda. \end{aligned}\]2)猜测第 0 步的控制量。因为 $\lambda(1) = 1$ ,要让 $\nabla J = u(1)+\lambda(1) = 0$,那么有 $u(1)=0$。不妨先设 $u^0(t)=0$。
代码实现如下。
u = -0.0*ones(1, t_segment); % 控制量的初值猜测
3)正向积分求 $x(t)$。把 $u^0(t)=0$ 代入状态方程中,为$x^0 = -(x^0)^2$。随后进行积分,并结合初值 $x^0(0)=10$,求得
\[x^0(t)=\frac{10}{1+10t}.\]代码实现如下。
% 1) 正向积分状态方程得到 x(t)
[Tx, X] = ode45(@(t,x) stateEq(t,x,u,Tu), [t0 tf], initx, options);
x = X;
% 状态方程
function dx = stateEq(t,x,u,Tu)
u = interp1(Tu,u,t);
dx = -x^2+u;
end
4)反向积分求 $\lambda(t)$。把 $x^0(t)=\frac{10}{1+10t}$ 代入伴随方程中,得到
\[\dot \lambda^0(t) = \frac{20}{1+10t}\lambda^0 - \frac{10}{1+10t},\]结合末值条件 $\lambda(1) = 0$,得到
\[\lambda^0(t) = 0.5 \left[1 - \frac{(1+10t)^2}{121} \right].\]代码实现如下。
% 2) 反向积分协态方程得到 p(t)
% 注意这里的时间区间!它是反的!意思就是反向积分!
[Tp, P] = ode45(@(t,p) costateEq(t,p,x,Tx), [tf, t0], initp, options);
p = P;
% 因为求得的协态变量按照时间反序排列,为保证 x 和 p 在同一时间序列下
% 需要调整其顺序
p =interp1(Tp,p,Tx);
% 协态方程
function dp = costateEq(t,p,x,Tx)
x = interp1(Tx,x,t);
dp = -x + 2*p.*x;
end
5)计算梯度。将 $u^0(t)=0$ 和 $\lambda^0(t)=0.5 \left[1 - \frac{(1+10t)^2}{121} \right]$ 代入 $\nabla J = u+\lambda$ 中,得到
\[\nabla J(u^0) = 0.5 \left[1 - \frac{(1+10t)^2}{121} \right].\]代码实现如下。
% 计算 dH/du,即目标泛函的梯度deltaH
dH = gradient(p,Tx,u,Tu);
H_Norm(i,1) = dH'*dH; % 为后面判断是否满足终止条件做准备
% 用梯度法求解 dH/du 的表达式
function dH = gradient(p,Tx,u,Tu)
u = interp1(Tu,u,Tx);
dH = p + u;
end
6)确定步长和修改量。在本算例中,将步长定为 $K=0.55$2,那么控制修改量为
\[\Delta u^0(t) = - 0.275 \left[1 - \frac{(1+10t)^2}{121} \right].\]计算性能指标,为
\[\nabla J(u^0) = -\frac{1}{4}\int_{0}^{1} \left[1 - \frac{(1+10t)^2}{121} \right]^2 \text{d}t.\]代码实现如下。
% 更新控制量(梯度法)
% 计算目标函数的值
J(i,1) = fun(tf,x,Tx,u,Tu);
fprintf('The value of the objective function is %.4f \n',J(i,1))
% 如果梯度 dH/du < epsilon,则退出循环
if H_Norm(i,1) < eps
break;
else
% 否则,更新控制量,进入下一次迭代
u_old = u;
u = control_update_by_gradient(dH,Tx,u_old,Tu,step(i,1));
end
function u_new = control_update_by_gradient(dH,tx,u,tu,step)
K = 0.55;
dH = interp1(tx,dH,tu);
u_new = u - K*dH;
end
7)更新控制量。按照 $u^1(t)=u^0(t)+\Delta u^0(t)$ 更新控制量,为
\[u^1(t) = - 0.275 \left[1 - \frac{(1+10t)^2}{121} \right].\]代码在第6)步已经给出。
8)循环迭代。按照上述步骤循环迭代3)—7)步,直至满足条件要求 H_Norm(i,1)<eps 或者迭代次数达到设定上限。
代码
前面给的代码是部分代码,在这里给出完整代码。
此代码我做了一些修改,主要有:
- 把步长改为了变步长,使用一维线搜索技术确定步长。使用
armijo准则来搜索步长。 - 添加了共轭梯度法的最优控制解法,跟梯度法做个对比。
control_update_by_gradient()为梯度法,control_update_by_conjugate_gradient()为共轭梯度法。
%--------------------------------------------------------------------------
% 说明:应用最速下降法求解最优控制问题
% 例子:《最优化与最优控制》 pp. 257 例13.1
% 类型:无控制约束的最优控制问题
% 时间:2022/06/25
%--------------------------------------------------------------------------
clear;clc;close all;
%% 主函数部分
eps = 1e-3;
options = odeset('RelTol', 1e-4, 'AbsTol',1e-4);
t0 = 0; tf = 1;
t_segment = 50;
Tu = linspace(t0, tf, t_segment); % 将时间离散化
u = -0.0*ones(1, t_segment); % 控制量的初值猜测
initx = 10; % 状态变量初值
initp = 0.1; % 协态变量初值
max_iteration = 50; % 最大迭代次数
H_Norm = zeros(max_iteration,1);
step = 0.55*ones(max_iteration,1);
J = zeros(max_iteration,1);
d = zeros(max_iteration,max_iteration);
%% 算法开始
tic;
for i = 1:max_iteration
disp('---------------------------');
fprintf('%d iterarion times \n',i)
% 1) 正向积分状态方程得到 x(t)
[Tx, X] = ode45(@(t,x) stateEq(t,x,u,Tu), [t0 tf], initx, options);
% 2) 反向积分协态方程得到 p(t)
x = X;
[Tp, P] = ode45(@(t,p) costateEq(t,p,x,Tx), [tf, t0], initp, options);
p = P;
% 因为求得的协态变量按照时间反序排列,为保证 x 和 p 在同一时间序列下
% 需要调整其顺序
p =interp1(Tp,p,Tx);
% 计算 dH/du,即目标泛函的梯度deltaH
dH = gradient(p,Tx,u,Tu);
H_Norm(i,1) = dH'*dH;
% 计算目标函数的值
J(i,1) = fun(tf,x,Tx,u,Tu);
fprintf('The value of the objective function is %.4f \n',J(i,1))
% 如果梯度 dH/du < epsilon,则退出循环
if H_Norm(i,1) < eps
% 显示最后一次的目标函数值
% fprintf('The value of the objective function is %.4f \n',J(i,1))
break;
else
% 否则,更新控制量,进入下一次迭代
u_old = u;
% 计算更新步长
% 我发现步长的影响更大,使不使用armijo线搜索来搜索步长对结果影响不大(beta = 0.55)
% step = 0.1*ones(max_iteration,1) 时,用梯度法更新 u 的迭代次数为 39 次,共轭梯度法为 14 次
% step = 0.55*ones(max_iteration,1) 时,用梯度法更新 u 的迭代次数为 5 次,共轭梯度法为 6 次
% 而step = 0*ones(max_iteration,1) 时,用armijo线搜索来搜索步长,
% 则梯度法更新 u 的迭代次数为 6 次,共轭梯度法为 13 次
% step(i,1) = armijo(u_old, -dH, tf, x, Tx, Tu);
u = control_update_by_gradient(dH,Tx,u_old,Tu,step(i,1));
% [u,d] = control_update_by_conjugate_gradient(H_Norm,dH,d,Tx,u_old,Tu,step(i,1),i);
end
end
if i == max_iteration
disp('---------------------------');
disp('已达最大迭代次数,停止算法.');
end
toc;
%% 画图
window_width = 500;
window_height = 416;
figure('color',[1 1 1],'position',[300,200,window_width,window_height]);
plot(Tx, X, 'x-','LineWidth',1.5);hold on;
plot(Tu, u, 'x-','LineWidth',1.5);
xlabel('Time');
ylabel('State & control');
set(gca,'FontSize',15,...
'FontName','Times New Roman',...
'LineWidth',1.5);
legend('$x(t)$','$u(t)$',...
'Location','Northeast',...
'FontSize',10,...
'interpreter','latex');
count = find(J==0);
if isempty(count)
t_plot = (1:length(J))';
J_plot = J;
else
if J(count(1)-1)-J(count(1)) > 1
t_plot = (1:count(1)-1)';
J_plot = J(1:count-1);
else
t_plot = (1:length(J))';
J_plot = J;
end
end
figure('color',[1 1 1],'position',[300+window_width,200,window_width,window_height]);
plot(t_plot,J_plot,'x-','LineWidth',1.5);
xlabel('Iterations');
ylabel('J');
set(gca,'FontSize',15,...
'FontName','Times New Roman',...
'LineWidth',1.5);
legend('$J$',...
'Location','Northeast',...
'FontSize',10,...
'interpreter','latex');
%% 子函数定义部分
% 状态方程
function dx = stateEq(t,x,u,Tu)
u = interp1(Tu,u,t);
dx = -x^2+u;
end
% 协态方程
function dp = costateEq(t,p,x,Tx)
x = interp1(Tx,x,t);
dp = -x + 2*p.*x;
end
% 用梯度法求解 dH/du 的表达式
function dH = gradient(p,Tx,u,Tu)
u = interp1(Tu,u,Tx);
dH = p + u;
end
% 更新控制量(梯度法)
function u_new = control_update_by_gradient(dH,tx,u,tu,step)
beta = 0.55;
dH = interp1(tx,dH,tu);
% 用armijo准则搜索步长
u_new = u - beta^step*dH;
% 不用armijo准则搜索步长
% u_new = u - step*dH;
end
% 更新控制量(共轭梯度法)
function [u_new,d] = control_update_by_conjugate_gradient(H_Norm,dH,d,tx,u,tu,step,i)
beta = 0.55;
dH = interp1(tx,dH,tu);
if i == 1
d(:,i) = -dH;
else
beta = H_Norm(i)/H_Norm(i-1);
d(:,i) = -dH' + beta*d(:,i-1);
end
% 用armijo准则搜索步长
u_new = u + beta^step*d(:,i)';
% 不用armijo准则搜索步长
% u_new = u + step*d(:,i)';
end
%--------------------------------------------------------------------------
% 说明:armijo准则非精确线搜索程序,用来求解迭代步长
% 文献:《最优化方法及其Matlab程序设计》 pp. 26
% 作者:袁亚湘
%--------------------------------------------------------------------------
function mk = armijo(xk, dk, tf, x, Tx, Tu)
dk = -interp1(Tx,dk,Tu);
beta = 0.55;
sigma = 0.5;
m = 0;
mmax = 20;
while m <= mmax
if fun(tf,x,Tx,xk+beta^m*dk,Tu) <= fun(tf,x,Tx,xk+beta^m*dk,Tu)+sigma*beta^m*gfun(tf,xk,Tu)*dk'
m = m+1;
break;
end
m = m+1;
end
mk = m;
% 这个 end 归属于 function
end
function J = fun(tf,x,Tx,u,Tu)
J = tf*(((x')*x)/length(Tx) + (u*u')/length(Tu));
end
function gJ = gfun(tf,u,Tu)
gJ = tf*(2*u)/length(Tu);
end
结果
仿真结果图如下。
状态量和控制量变化曲线为
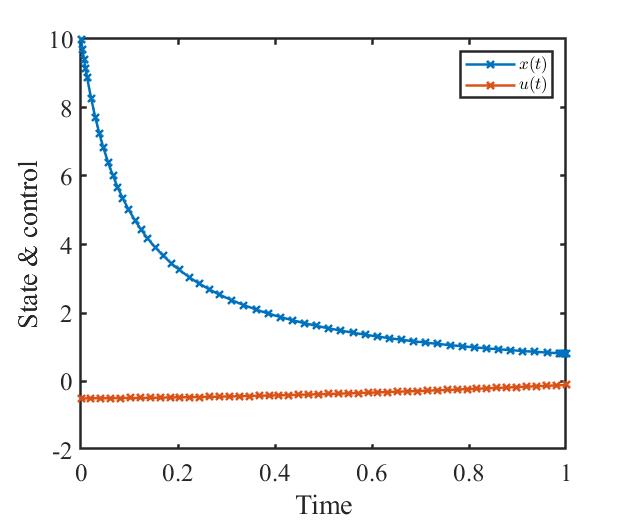
性能指标变化曲线为
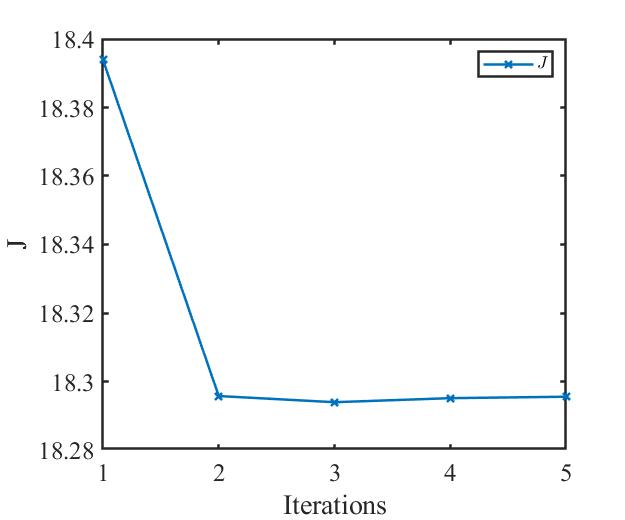
从性能指标的结果来看,梯度法迭代了5步就已经找到最优控制量 $u^*(t)$ 。
对比
为了不同算法、步长对于最优控制问题结果的影响,这里分别给出了3个对比实验的例子,分别是:
- 梯度法和共轭梯度法对比;
- 不同步长条件下的两种算法结果对比;
- 是否使用
armijo准则搜索步长的两种算法结果对比。
梯度法和共轭梯度法对比
共轭梯度法在完整代码中已经给出。共轭梯度法与梯度法的不同在于更新控制量的修改方向。梯度法是沿着负梯度方向修改控制量,共轭梯度法是沿着共轭梯度方向3修改控制量。《最优化与最优控制》第2版第268页中指出,“用共轭梯度法求最优控制,计算程序容易实现,计算可靠性好,收敛速度比梯度法快,特别是对于二次泛函性能指标的最优控制问题更为有效。”
出于对这句话的好奇,本文用matlab编写了共轭梯度法代码,与梯度法进行对比,验证共轭梯度法是不是真的“收敛速度比梯度法快”。
因为前面已经做过仿真了,可以看到最优控制 $u^*(0) \approx -0.5$,所以在代码是实现时令第1次迭代的控制量 $u^0(t)=-0.5$。代码如下。
u = -0.5*ones(1, t_segment); % 控制量的初值猜测
在这里步长更新不用armijo准则更新,使用定步长。代码如下。
step = 0.55*ones(max_iteration,1);
% 下面这一行代码在“算法开始”节中,记得注释
% step(i,1) = armijo(u_old, -dH, tf, x, Tx, Tu);
仿真结果如下。
状态量变化曲线为

控制量变化曲线为
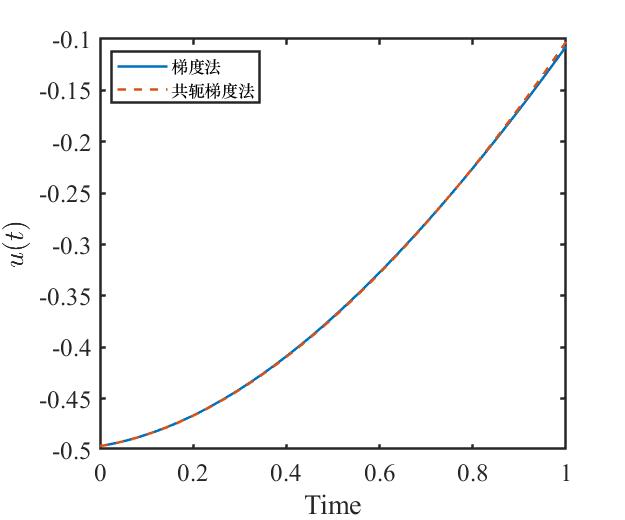
性能指标变化曲线为

可以看出,梯度法和共轭梯度法在求解本例最优控制问题中,所求得的控制量基本一致。所以由控制量决定的状态量也基本一致。
迭代次数也都是6次,不过共轭梯度法的性能指标下降速度更快一些,在第4步的时候甚至求得一个更小的性能指标。但因为在此步中没有满足终止条件,所以没有取到这个性能指标而是选择继续迭代。最终梯度法和共轭梯度法的性能指标都收敛于同一个值。
从上面的数值数值实验中,我们目前无法推断出“共轭梯度法收敛速度比梯度法快”的结论。原因可能在于步长选择得不太合适,或者该问题比较简单,无法突显共轭梯度法的优越性。
不同步长条件下的两种算法结果对比
这里分别选取步长为 0.01、0.1 和 0.55 进行实验,实验过程中分别使用梯度法和共轭梯度法求解最优控制问题。
因为梯度法和共轭梯度法在不同步长下得到的控制量与状态量变化曲线差异较小,可以参考前面部分的图,所以这里不再给出状态量和控制量的图。仅给出性能指标迭代图,专注于迭代次数和收敛速度的分析。
仿真结果如下。

注:$gm$ 代表梯度法, $cgm$ 代表共轭梯度法。
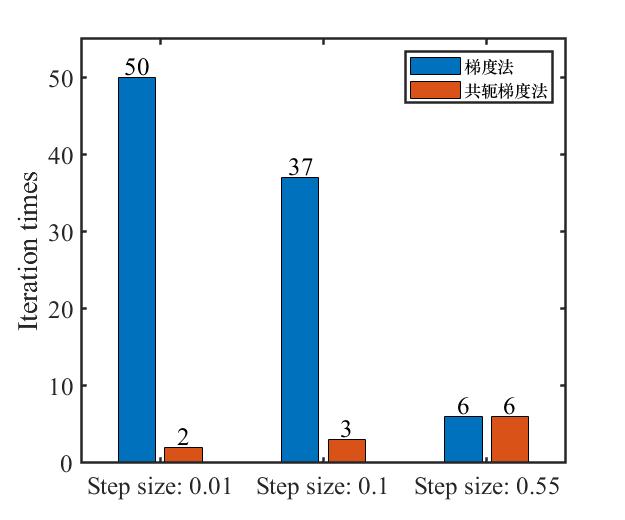
从图中可以看出,步长为0.55时,梯度法和共轭梯度法的迭代次数均为6次。
如果缩小迭代步长,例如将步长设置为0.01、0.1,共轭梯度法的优势就体现出来了。
步长为0.01时,梯度法迭代次数为50次4,且性能指标没有收敛到最优值;共轭梯度法迭代次数为2次,性能指标收敛。
步长为0.1时,梯度法迭代次数为37次,共轭梯度法迭代次数为3次,性能指标均收敛。
通过对比不同步长条件下梯度法和共轭梯度法的仿真结果,可以发现,当步长取得比较小的时候,共轭梯度法的收敛速度更快,梯度法则需要一步一步地迭代,收敛速度慢;当步长取得比较大的时候,梯度法和共轭梯度法的收敛速度相差不大。
是否使用armijo准则搜索步长的两种算法结果对比
下面设置初始步长为 0.55,armijo准则的搜索步长为 0.55,初始控制量为 $u^0(t)=-0.5$ ,分别采用梯度法和共轭梯度法进行实验。
仿真结果如下。

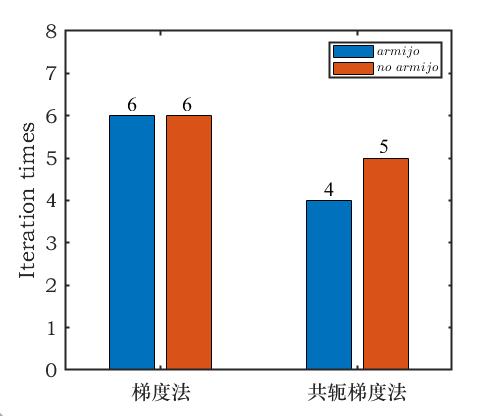
注:$gm$ 代表梯度法, $cgm$ 代表共轭梯度法;$armijo$ 代表使用armijo准则,$no \ armijo$ 代表不使用armijo准则。
从上面两张图可以看出,对于这个算例来说,两种算法使用和不使用armijo准则的迭代次数相差无几。
梯度法中,使用armijo准则和不适用armijo准则的迭代次数均为6次;共轭梯度法中,使用armijo准则的迭代次数为4次,不使用armijo准则的迭代次数为5次,略有区别,但区别不大。
对于是否使用armijo准则来搜索步长这个问题,还需要更多的算例来研究。
思考
一开始准备用matlab的数学工具箱来求这个最优控制问题的解析解的,但是发现这样一个简单的最优控制问题,用解析法来求都十分地困难,更不用说状态方程和约束条件更加复杂的最优控制问题了。所以开始考虑用数值解法来解这些问题。
选了最简单的梯度法尝试求解最优控制问题。但是在求解过程中发现自己从头到尾写代码就很难写对,一直报错。于是转换思路在网络上找找有没有开源的代码用,真的在mathwork的file exchange里找到了梯度法的代码。研究了一下代码,改换成了我要解决的问题,发现这个代码效果挺好的。
我发现了,当自己代码写不出来的时候,就该在网络上找找有没有合用的代码。开源这件事情很重要,能够帮助到有同样问题的后来者少走弯路,所以决心把自己解决这个问题的过程记录下来,把代码分享出去。