双方叫价拍卖:一种贝叶斯博弈均衡的解法
[TOC]
一、数学模型:双方叫价拍卖模型
考虑一类双方叫价拍卖(double auction),潜在的卖方和买方同时开价,卖方提出要价(asking price),买方提出出价(bidding price),拍卖商选择成交价格$p$清算市场。交易规则为
- 所有要价低于$p$的卖方卖出,所有出价高于$p$的买方买入;
- 在价格$p$下的总供给等于总需求。
查特金和萨缪尔逊(Chatterjee and Samuelson,1983)建立了一个简单双方叫价拍卖模型。
该模型中,有一个卖方和一个买方。卖方提供该商品的成本为$c$,或者说,该商品对卖方的价值为$c$;该商品对买方的价值为$v$。
注:$c \in [0,1]$,$v \in [0,1]$。
该模型的具体流程为
同时地,卖方提出要价$p_s \in [0,1]$,买方提出出价$p_b \in [0,1]$;
若$p_b \ge p_s$,双方在$p = (p_s+p_b)/2$上成交;卖方的博弈收益为$u_s = (p_s + p_b)/2 -c$,买方的博弈收益为$u_b = v - (p_b+p_s)$;
若$p_b < p_s$,没有交易发生;卖方和买方的效用均为$0$。
二、问题描述:贝叶斯博弈模型
现在考虑不完全信息的情况,即
- 只有卖方知道$c$(卖方提供该商品的成本);
- 只有买方知道$v$(该商品对买方的价值);
- $c$和$v$在$[0,1]$均匀分布,概率分布函数$f(x)=1/(b-a) \quad x \in [a,b]$为公共知识。
在该贝叶斯博弈中,卖方的策略(即要价)$p_s$是$c$的函数,为$p_s(c)$;买方的策略(即出价)$p_b$是$v$的函数,为$p_b(v)$。策略组合$(p_s^*(c),p_b^*(v))$是一个贝叶斯均衡(Bayesian Nash Equilibrium,BNE),假定下列两个条件成立:
-
卖方最优:对于所有的$c \in [0,1]$,$p_s^*(c)$是下列最优化问题的解,为
\[\max_{p_s} u_s = \max_{p_s}\left [ \frac{1}{2}(p_s + \text{E}[p_b(v)|p_b(v) \ge p_s]) - c \right ]\cdot \text{Prob}\{ p_b(v) \ge p_s \}\]式中,$\text{E}[p_b(v)|p_b(v) \ge p_s]$为给定买方的出价高于卖方的要价的条件下,卖方预期买方的出价。
-
买方最优:对于所有的$v \in [0,1]$,$p_b^*(c)$是下列最优化问题的解,为
\[\max_{p_b} u_b = \max_{p_b}\left [v- \frac{1}{2}(p_b + \text{E}[p_s(c)|p_b \ge p_s(c)])\right ]\cdot \text{Prob}\{ p_b \ge p_s(c) \}\]式中,$\text{E}[p_s(c)|p_b \ge p_s(c)]$为给定买方的出价高于卖方的要价的条件下,买方预期卖方的要价。
问题1:为什么会有上述两个目标函数的形式?
回答:见前文提到的模型流程,在$p_b \ge p_s$的条件下,双方在$p = (p_s+p_b)/2$上成交。卖方的博弈收益为$u_s = (p_s + p_b)/2 -c$,$p_s$是卖方可以确定的变量,那么$p_b$要满足$p_b \ge p_s$的条件,所以要计算$p_b$在$p_b \ge p_s$内的期望博弈收益,写为$\text{E}[p_b(v)|p_b(v) \ge p_s]$。
买方的博弈收益为$u_b = v - (p_b+p_s)$,$p_b$是买方可以确定的变量,那么$p_s$要满足$p_b \ge p_s$的条件所以要计算$p_s$在$p_b \ge p_s$内的期望博弈收益,写为$\text{E}[p_s(c)|p_b \ge p_s(c)]$。
三、理论方法:贝叶斯均衡的解法
该贝叶斯博弈有多种BNE,首先考虑一类线性策略均衡,表达式为
\[\left \{\begin{aligned} &p_s(c) = \alpha_s + \beta_s c, \\ &p_b(v) = \alpha_b + \beta_b c. \end{aligned}\right.\]3.1 求解卖方的目标函数
先求解卖方的目标函数,为此,要先求解下面两个式子,分别是
\[\text{Prob}\{p_b(v) \ge p_s \}\]和
\[\text{E}[p_b(v)|p_b(v) \ge p_s]\]3.1.1 求解$\text{Prob}{p_b(v) \ge p_s }$
可以将买方出价$p_b(v)$大于等于卖方要价$p_s$的概率表示为
\[\text{Prob}\{p_b(v) \ge p_s\} = \text{Prob}\{\alpha_b + \beta_b v \ge p_s\}.\]随后,解不等式$\alpha_b + \beta_b v \ge p_s$,为
\[v \ge \frac{p_s - \alpha_b}{\beta_b}.\]由于$v$在$[0,1]$上均匀分布,因此$v$大于等于$\frac{p_s - \alpha_b}{\beta_b}$的概率为
\[\text{Prob}\left\{v \ge \frac{p_s - \alpha_b}{\beta_b}\right\} = 1 - \frac{p_s - \alpha_b}{\beta_b},\]化简得到下式,为
\[\text{Prob}\{p_b(v) \ge p_s\} = (\alpha_b + \beta_b - p_s) / \beta_b.\]3.1.2 求解$\text{E}[p_b(v)|p_b(v) \ge p_s]$
根据条件期望的定义(见附录),而且根据条件概率$p_b(v) \ge p_s$,得到积分上限为$\alpha_b+\beta_b$,积分下限为$p_s$,因为$p_b(v)$在$[\alpha_b, \alpha_b + \beta_b]$上均匀分布,得到
\[\text{E}\{p_b(v) | p_b(v) \ge p_s\} = \frac{\int_{p_s}^{\alpha_b + \beta_b} x f(x) \text{d}x}{\text{Prob}\{p_b(v) \ge p_s\}},\]其中,$f(x)$是$p_b(v)$的概率密度函数。由于$p_b(v)$在$[\alpha_b, \alpha_b + \beta_b]$上均匀分布,因此$f(x) = \frac{1}{\beta_b}$。代入上式,为
\[\text{E}\{p_b(v) | p_b(v) \ge p_s\} = \frac{\frac{1}{\beta_b} \int_{p_s}^{\alpha_b + \beta_b} x \text{d}x}{\text{Prob}\{p_b(v) \ge p_s\}},\]计算积分$\int_{p_s}^{\alpha_b + \beta_b} x \text{d}x$,为
\[\int_{p_s}^{\alpha_b + \beta_b} x \text{d}x = \left. \frac{x^2}{2} \right|_{p_s}^{\alpha_b + \beta_b} = \frac{(\alpha_b + \beta_b)^2}{2} - \frac{p_s^2}{2},\]代入上式,为
\[\text{E}\{p_b(v) | p_b(v) \ge p_s\} = \frac{\frac{1}{\beta_b} \left( \frac{(\alpha_b + \beta_b)^2}{2} - \frac{p_s^2}{2} \right)}{\frac{\alpha_b + \beta_b - p_s}{\beta_b}},\]化简为
\[\text{E}\{p_b(v) | p_b(v) \ge p_s\} = \frac{(\alpha_b + \beta_b)^2 - p_s^2}{2(\alpha_b + \beta_b - p_s)},\]进一步得到
\[\text{E}\{p_b(v) | p_b(v) \ge p_s\} = 0.5 (p_s + \alpha_b + \beta_b).\]3.1.3 求解卖方的目标函数
将得到的$\text{Prob}{p_b(v) \ge p_s} = (\alpha_b + \beta_b - p_s)/\beta_b$和$\text{E}{p_b(v) | p_b(v) \ge p_s} = 0.5 (p_s + \alpha_b + \beta_b)$代入卖方的目标函数,有
\[\begin{aligned} & \max_{p_s}\left [ \frac{1}{2}(p_s + \text{E}[p_b(v)|p_b(v) \ge p_s]) - c \right ]\cdot \text{Prob}\{ p_b(v) \ge p_s \}, \\ \Rightarrow & \max_{p_s}\left [ \frac{1}{2}(p_s + \frac{1}{2} (p_s + \alpha_b + \beta_b)) - c \right ]\cdot (\alpha_b + \beta_b - p_s), \\ \Rightarrow & \max_{p_s}\left [ \frac{1}{2}(p_s + \frac{1}{2} p_s + \frac{1}{2} \alpha_b + \frac{1}{2} \beta_b) - c \right ]\cdot (\alpha_b + \beta_b - p_s), \\ \Rightarrow & \max_{p_s}\left [\frac{3}{4} p_s + \frac{1}{4} \alpha_b + \frac{1}{4} \beta_b - c \right ]\cdot (\alpha_b + \beta_b - p_s), \\ \end{aligned}\]对$p_s$求偏导,获得一阶最优化条件,为
\[\begin{aligned} \frac{\partial u_s}{\partial p_s} &= \frac{\partial \left [\frac{3}{4} p_s + \frac{1}{4} \alpha_b + \frac{1}{4} \beta_b - c \right ]\cdot (\alpha_b + \beta_b - p_s)}{\partial p_s}, \\ &= \frac{3}{4} \cdot \frac{\alpha_b + \beta_b - p_s}{\beta_b} - \frac{1}{\beta_b} (\frac{3}{4} p_s + \frac{1}{4} \alpha_b + \frac{1}{4} \beta_b - c), \\ &= \frac{3}{4\beta_b} \cdot (\alpha_b + \beta_b - p_s) - \frac{3}{4\beta_b} (p_s + \frac{1}{3}\alpha_b + \frac{1}{3}\beta_b - \frac{4c}{3}), \\ &= \frac{3}{4\beta_b} \cdot (\frac{2}{3}\alpha_b + \frac{2}{3}\beta_b - 2p_s + \frac{4c}{3}). \end{aligned}\]令
\[\frac{\partial u_s}{\partial p_s} = \frac{3}{4\beta_b} \cdot (\frac{2}{3}\alpha_b + \frac{2}{3}\beta_b - 2p_s + \frac{4c}{3}) = 0,\]前者不会为$0$,只能让后者为$0$,有
\[\frac{2}{3}\alpha_b + \frac{2}{3}\beta_b - 2p_s + \frac{4c}{3} = 0,\]化简得到
\[\boxed{p_s = \frac{1}{3}(\alpha_b + \beta_b) + \frac{2}{3}c.}\]3.2 求解买方的目标函数
再求解买方的目标函数,同样地,要先求解下面两个式子,分别是
\[\text{Prob}\{p_b \ge p_s(c) \}\]和
\[\text{E}[p_s(c)|p_b \ge p_s(c)]\]3.2.1 求解$\text{Prob}{p_b \ge p_s(c) }$
可以将买方出价$p_b$大于等于卖方要价$p_s(c)$的概率表示为
\[\text{Prob}\{p_b \ge p_s(c)\} = \text{Prob}\{p_b \ge \alpha_s + \beta_s c\}.\]随后,解不等式$p_b \ge \alpha_s + \beta_s c$,为
\[c \le \frac{p_b - \alpha_s}{\beta_s}.\]由于$c$在$[0,1]$上均匀分布,因此$c$小于等等于$\frac{p_b - \alpha_s}{\beta_s}$的概率为
\[\text{Prob}\left\{c \le \frac{p_b - \alpha_s}{\beta_s}\right\} = \frac{p_b - \alpha_s}{\beta_s},\]化简得到下式,为
\[\text{Prob}\{p_b \ge p_s(c) \} = (p_b - \alpha_s)/\beta_s.\]3.2.2 求解$\text{E}[p_s(c)|p_b \ge p_s(c)]$
根据条件期望的定义(见附录),而且根据条件概率$p_b \ge p_s(c)$,得到积分上限为$p_b$,积分下限为$\alpha_s$,因为$p_s(c)$在$[\alpha_s, \alpha_s + \beta_s]$上均匀分布,得到
\[\text{E}[p_s(c)| p_b \ge p_s(c)] = \frac{\int_{\alpha_s}^{p_b} x f(x) \text{d}x}{\text{Prob}\{p_b \ge p_s(c)\}},\]其中,$f(x)$是$p_s(c)$的概率密度函数。由于$p_s(c)$在$[\alpha_s, \alpha_s + \beta_s]$上均匀分布,因此$f(x) = \frac{1}{\beta_s}$。代入上式,为
\[\text{E}\{p_b(v) | p_b \ge p_s(c)\} = \frac{\frac{1}{\beta_s} \int_{\alpha_s}^{p_b} x \text{d}x}{\text{Prob}\{p_b \ge p_s(c)\}},\]计算积分$ \int_{\alpha_s}^{p_b} x \text{d}x$,为
\[\int_{\alpha_s}^{p_b} x \text{d}x = \left. \frac{x^2}{2} \right|_{\alpha_s}^{p_b} = \frac{p_b^2-\alpha_s^2}{2},\]代入上式,为
\[\text{E}\{p_b(v) | p_b \ge p_s(c)\} = \frac{\frac{1}{\beta_b} \left( \frac{p_b^2-\alpha_s^2}{2} \right)}{\frac{p_b - \alpha_s}{\beta_s}},\]化简为
\[\text{E}\{p_b(v) | p_b \ge p_s(c)\} = \frac{(p_b - \alpha_s)(p_b + \alpha_s)}{2(p_b - \alpha_s)},\]进一步得到
\[\text{E}\{p_b(v) | p_b \ge p_s(c)\} = 0.5 (p_b + \alpha_s).\]3.2.3 求解买方的目标函数
将得到的$\text{Prob}{p_b \ge p_s(c) } = (p_b - \alpha_s)/\beta_s$和$\text{E}{p_b(v) | p_b \ge p_s(c)} = 0.5 (p_b + \alpha_s)$代入卖方的目标函数,有
\[\begin{aligned} & \max_{p_b}\left [v- \frac{1}{2}(p_b + \text{E}[p_s(c)|p_b \ge p_s(c)])\right ]\cdot \text{Prob}\{ p_b \ge p_s(c) \}, \\ \Rightarrow & \max_{p_b}\left [v- \frac{1}{2}(p_b + \frac{1}{2} (p_b + \alpha_s))\right ]\cdot (p_b - \alpha_s)/\beta_s, \\ \Rightarrow & \max_{p_b}\left [v- \frac{1}{2}(p_b + \frac{1}{2}p_b + \frac{1}{2}\alpha_s)\right ]\cdot (p_b - \alpha_s)/\beta_s, \\ \Rightarrow & \max_{p_b}\left [v- \frac{1}{2}(\frac{3}{2}p_b + \frac{1}{2}\alpha_s)\right ]\cdot (p_b - \alpha_s)/\beta_s, \\ \Rightarrow & \max_{p_b}\left [v- \frac{3}{4}p_b - \frac{1}{4}\alpha_s \right ]\cdot (p_b - \alpha_s)/\beta_s, \\ \end{aligned}\]对$p_s$求偏导,获得一阶最优化条件,为
\[\begin{aligned} \frac{\partial u_b}{\partial p_b} &= \frac{\partial \left [v- \frac{3}{4}p_b - \frac{1}{4}\alpha_s \right ]\cdot (p_b - \alpha_s)/\beta_s}{\partial p_b}, \\ &= -\frac{3}{4} \frac{p_b-\alpha_b}{\beta_s} + \frac{1}{\beta_s}(v - \frac{3}{4}p_b - \frac{1}{4}\alpha_s), \\ &= \frac{3}{4 \beta_s}(\alpha_b-p_b) + \frac{3}{4\beta_s}(\frac{4}{3}v - p_b - \frac{1}{3}\alpha_s), \\ &= \frac{3}{4 \beta_s}(\frac{2}{3}\alpha_b - 2 p_b + \frac{4}{3}v) \end{aligned}\]令
\[\frac{\partial u_s}{\partial p_s} = \frac{3}{4 \beta_s}(\frac{2}{3}\alpha_b - 2 p_b + \frac{4}{3}v) = 0,\]前者不会为$0$,只能让后者为$0$,有
\[\frac{2}{3}\alpha_b - 2 p_b + \frac{4}{3}v = 0,\]化简得到
\[\boxed{p_b = \frac{1}{3}\alpha_s + \frac{2}{3}v.}\]3.3 求解BNE
重写一遍卖家和买家的一阶最优化条件,为
\[\left \{\begin{aligned} &p_s(c) = \frac{1}{3}(\alpha_b + \beta_b) + \frac{2}{3}c, \\ &p_b(v) = \frac{1}{3}\alpha_s + \frac{2}{3}v. \end{aligned}\right.\]再列出$p_s(c)$和$p_b(v)$,方便对比,为
\[\left \{\begin{aligned} &p_s(c) = \alpha_s + \beta_s c, \\ &p_b(v) = \alpha_b + \beta_b v. \end{aligned}\right.\]通过目测法,可以观察得到
\[\left \{\begin{aligned} \beta_s = \frac{2}{3},\\ \beta_b = \frac{2}{3}. \end{aligned}\right.\]把$\beta_s$和$\beta_b$代入卖家和买家的一阶最优化条件,得到
\[\left \{ \begin{aligned} &\frac{1}{3}\alpha_s = \alpha_b,\\ &\frac{1}{3}(\alpha_b+\frac{2}{3}) = \alpha_s. \end{aligned}\right.\]联立求解,得到
\[\left \{\begin{aligned} &\alpha_s = \frac{1}{4},\\ &\alpha_b = \frac{1}{12}. \end{aligned}\right.\]那么,卖方和买方的BNE为
\[\left \{\begin{aligned} &p_s(c) = \frac{1}{4} + \frac{2}{3} c, \\ &p_b(v) = \frac{1}{12} + \frac{2}{3} v. \end{aligned}\right.\]四、结果分析
4.1 卖方的策略
对于卖方而言,令要价小于成本,有
\[\frac{1}{4} + \frac{2}{3}c < c \Rightarrow c > \frac{3}{4}\]意为当$c > 3/4$时,卖方的要价低于成本,这对卖方来说不划算。
买方的最高报价为$p_b(1) = 1/12+2/3= 3/4$,等于卖方的要价均衡点$p_s(3/4)=1/4+2/3\cdot 3/4=3/4$。也就是说,卖方在$c>3/4$给出要价,成本会比要价高,卖方不会这样行动,故买卖双方的最高要价/出价不会高于$3/4$。
所以,卖方要价低于成本的情况不会出现。
4.2 买方的策略
对于买方而言,令出价高于成本,有
\[\frac{1}{12} + \frac{2}{3}v > v \Rightarrow v < \frac{1}{4}\]意为当$v < 1/4$时,买方的出价高于成本,这对买方来说不划算。
卖方的最低报价为$p_s(0) = 1/4$,等于买方的出价均衡点$p_b(1/4)=1/12+2/3\cdot 1/4=1/4$。也就是说,买方在$v<1/4$给出出价,成本会比出价低,买方不会这样行动,故买卖双方的最低要价/出价不会低于$1/4$。
所以,买方出价高于成本的情况不会出现。
4.3 BNE
在均衡情况下,当且仅当买方的出价大于等于卖方的要价时,即
\[(p_s^*(c),p_b(v)) \le (p_s^*(c),p_b^*(v)) \le (p_s^*(c),p_b(v))\]写得更加清晰一些,为
\[\begin{aligned} & p_s^*(c) \le p_b^*(v) \\ \Rightarrow & \alpha_s + \beta_s c \le \alpha_b + \beta_s v \\ \Rightarrow & \frac{1}{4} + \frac{2}{3} c \le \frac{1}{12} + \frac{2}{3} c \\ \Rightarrow & c + \frac{1}{4} \le v \end{aligned}\]满足上述条件,买卖双方才会发生交易。
那么,可以画出买卖双方的均衡线性策略图,如下图所示。
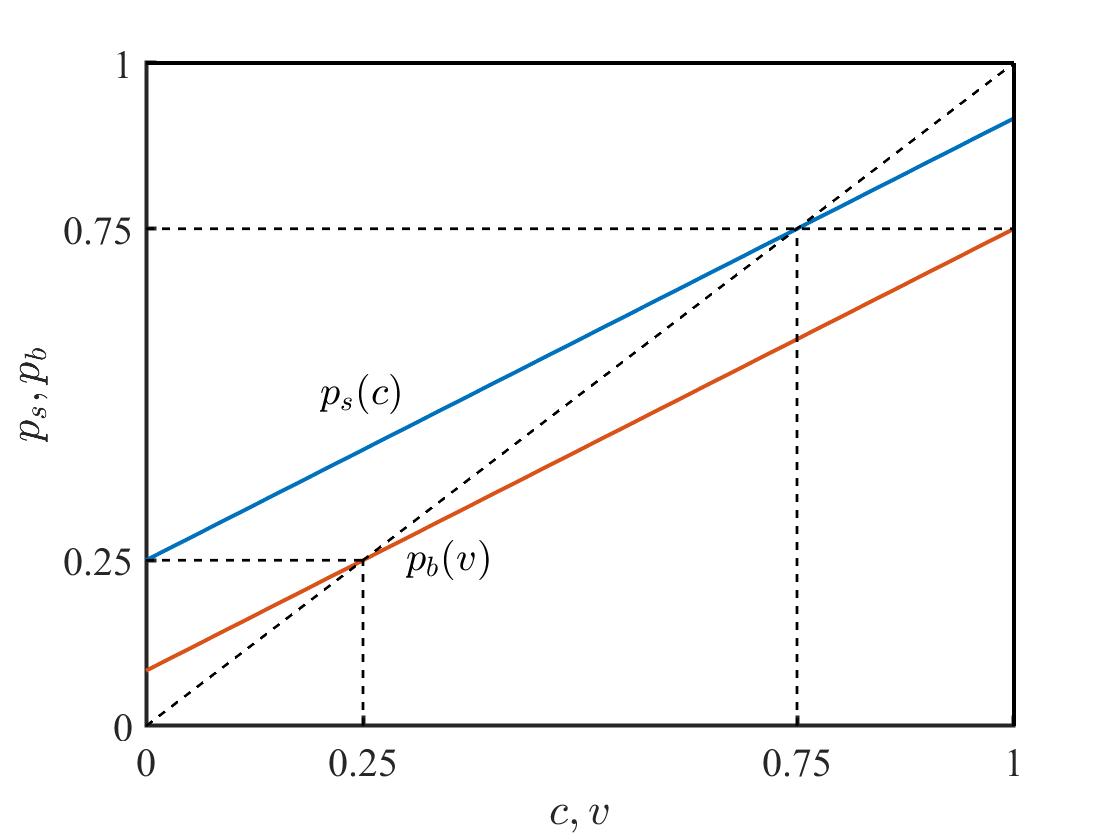
画出交易可行区域,如下图所示。
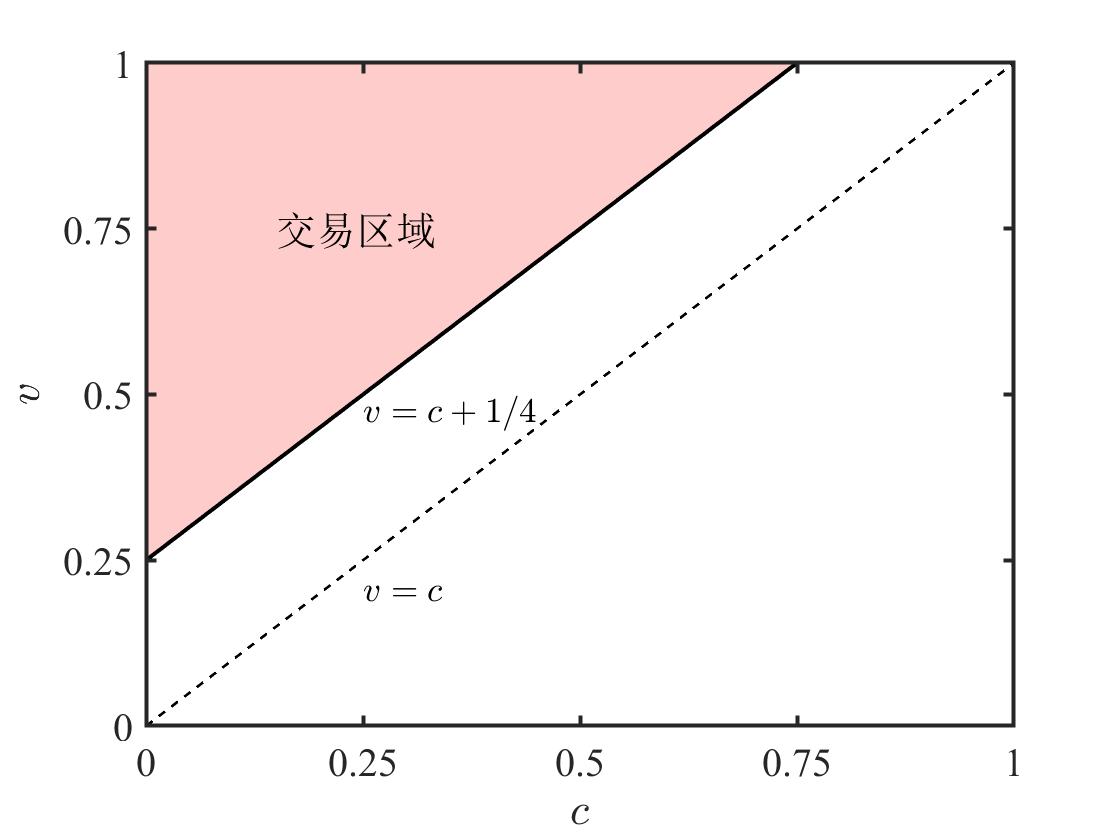
画图所用代码记录在下面,以防忘记。
clc;clear;close all;
%% 参数设置
c = 0:1e-2:1;
v = 0:1e-2:1;
ps = 1/4 + 2/3 .* c;
pb = 1/12 + 2/3 .* v;
%% 画图--均衡线性策略
figure('color',[1,1,1]);
plot(c,ps,'LineWidth',1.5);hold on;box off;
plot(v,pb,'LineWidth',1.5);
text(0.2,0.5,'$p_s(c)$','Interpreter','Latex','FontSize',15)
text(0.3,0.25,'$p_b(v)$','Interpreter','Latex','FontSize',15)
plot([0 1],[0 1],'k--','LineWidth',1);
plot([0,1/4],[1/4,1/4],'k--','LineWidth',1);
plot([1/4,1/4],[0,1/4],'k--','LineWidth',1);
plot([0,1],[3/4,3/4],'k--','LineWidth',1);
plot([3/4,3/4],[0,3/4],'k--','LineWidth',1);
plot([0,1],[1,1],'LineWidth',1.5,'color','black');
plot([1,1],[1,0],'LineWidth',1.5,'color','black');
xlabel('$c,v$','Interpreter','Latex');
ylabel('$p_s,p_b$','Interpreter','Latex');
xticks([0 1/4 3/4 1]);
yticks([0 1/4 3/4 1]);
set(gca,'FontName','Times New Roman','FontSize',15,'LineWidth',1.5);
%% 画图--交易区域
v = c+1/4;
figure('color',[1,1,1]);
fill([0 0 3/4],[1/4 1 1],'r','edgecolor',[1,1,1],'FaceAlpha',0.2);hold on;box on;
plot(c,v,'k','LineWidth',1.5);
plot([0 1],[0 1],'k--','LineWidth',1);
xlabel('$v$','Interpreter','Latex');
ylabel('$c$','Interpreter','Latex');
xticks([0 1/4 1/2 3/4 1]);
yticks([0 1/4 1/2 3/4 1]);
axis([0 1 0 1])
set(gca,'FontName','Times New Roman','FontSize',15,'LineWidth',1.5);
text(0.15,0.75,'交易区域','FontSize',15)
text(0.25,0.47,'$v = c + 1/4$','Interpreter','Latex','FontSize',13)
text(0.25,0.2,'$v = c$','Interpreter','Latex','FontSize',13)
参考文献
[1] 张维迎. 博弈论与信息经济学 [M]. 上海: 上海人民出版社, 2013: 154-158.
附录
条件期望的定义:条件期望是概率论中的一个基本概念,它描述了在给定某些信息的情况下,一个随机变量的期望值。具体来说,设$X$和$Y$是两个随机变量,那么$X$在给定$Y=y$的条件下的期望值,记作$E[X|Y=y]$,定义为:$E[X|Y=y] = \sum_{x} x \cdot P(X=x|Y=y)$。对于连续随机变量,条件期望的定义类似,只是求和变成了积分:$E[X|Y=y] = \int_{-\infty}^{\infty} x \cdot f_{X|Y}(x|y) \text{d}x$。其中,$f_{X|Y}(x|y)$是$X$在给定$Y=y$的条件下的条件概率密度函数。