GPOPS-II教程(5): 月球探测器着陆最优控制问题
问题描述
参考文献:[1] Meditch J. On the problem of optimal thrust programming for a lunar soft landing[J]. IEEE Transactions on Automatic Control, 1964, 9(4): 477-484.
考虑一类月球探测器着陆最优控制问题,$x$为月球探测器与月心的矢径,其动力学方程为
\[\left \{ \begin{aligned} \ddot x &= - k \frac{\text{d}}{\text{d}t}(\ln \ m) - g,\\ \dot x & = -k \ln{\frac{m(t)}{m(0)}} - g t + x(0). \end{aligned}\right.\]令$x_1 = h$,$x_2 = v$,$x_3=m$,可以得到
\[\dot x_1 = v,\quad \dot x_2 = -\frac{k}{x_3}u-g,\quad \dot x_3=m,\quad u = \dot m.\]性能指标如下:
\[J = \int_{t_0}^{t_f} \dot m(t) \text{d}t = m(0) - m(t_f)\]化简之后,月球探测器落地动力学方程为
\[\left \{ \begin{aligned} \dot x_1 &= v,\\ \dot x_2 &= u - g. \end{aligned}\right.\]化简之后的性能指标为
\[J = \int_{t_0}^{t_f} u \text{d}t\]GPOPS代码
main function
%% 01.初始参数设置
%-------------------------------------------------------------------------%
%----------------------- 设置问题的求解边界 ------------------------------%
%-------------------------------------------------------------------------%
% 设置时间边界
t0min = 0;
t0max = 0;
tfmin = 0;
tfmax = 10;
% 设置状态初值
h0 = 10;
v0 = -2;
% 设置状态终值
hf = 0;
vf = 0;
% 设置状态边界
hmin = 0;
hmax = 20;
vmin = -10;
vmax = 10;
% 设置控制量边界
umin = 0;
umax = 3;
% 月球重力常数
setup.auxdata.g = 1.6;
%% 02.边界条件设置
%-------------------------------------------------------------------------%
%------------------------ 将求解边界设置于问题中 -------------------------%
%-------------------------------------------------------------------------%
setup.bounds.phase.initialstate.lower = [h0, v0];
setup.bounds.phase.initialstate.upper = [h0, v0];
setup.bounds.phase.state.lower = [hmin, vmin];
setup.bounds.phase.state.upper = [hmax, vmax];
setup.bounds.phase.finalstate.lower = [hf, vf];
setup.bounds.phase.finalstate.upper = [hf, vf];
setup.bounds.phase.control.lower = umin;
setup.bounds.phase.control.upper = umax;
setup.bounds.phase.integral.lower = -100;
setup.bounds.phase.integral.upper = 100;
setup.bounds.phase.initialtime.lower = t0min;
setup.bounds.phase.initialtime.upper = t0max;
setup.bounds.phase.finaltime.lower = tfmin;
setup.bounds.phase.finaltime.upper = tfmax;
%% 03.初值猜测
%-------------------------------------------------------------------------%
%------------------------------- 初值猜想 --------------------------------%
%-------------------------------------------------------------------------%
h_guess = [h0; hf];
v_guess = [v0; vf];
u_guess = [umin; umin];
t_guess = [t0min; 5];
setup.guess.phase.state = [h_guess, v_guess];
setup.guess.phase.control = u_guess;
setup.guess.phase.time = t_guess;
setup.guess.phase.integral = 10;
%% 04.设置GPOPS求解器参数
%-------------------------------------------------------------------------%
%---------------------------- 设置求解器参数 -----------------------------%
%-------------------------------------------------------------------------%
setup.name = 'Moon-Lander-OCP';
setup.functions.continuous = @mlocpContinuous;
setup.functions.endpoint = @mlocpEndpoint;
setup.nlp.solver = 'ipopt';
setup.derivatives.supplier = 'sparseCD';
setup.derivatives.derivativelevel = 'second';
setup.mesh.method = 'hp1';
setup.mesh.tolerance = 1e-4;
setup.mesh.maxiteration = 45;
setup.mesh.colpointsmax = 4;
setup.mesh.colpointsmin = 10;
setup.mesh.phase.fraction = 0.1*ones(1,10);
setup.mesh.phase.colpoints = 4*ones(1,10);
setup.method = 'RPMintegration';
% setup.method = 'RPMdifferentiation';
%% 05.求解
%-------------------------------------------------------------------------%
%----------------------- 使用 GPOPS2 求解最优控制问题 --------------------%
%-------------------------------------------------------------------------%
tic;
output = gpops2(setup);
toc;
%% 06.画图
solution = output.result.solution;
% 状态量
figure('Color',[1,1,1]);
plot(solution.phase.time, solution.phase.state,'-x','LineWidth',1.5);
xlabel('Time',...
'FontWeight','bold');
ylabel('State',...
'FontWeight','bold');
legend('Altitude','Velocity')
set(gca,'FontName','Times New Roman',...
'FontSize',15,...
'LineWidth',1.3);
print -dpng moonlander_state.png
% 控制量
figure('Color',[1,1,1]);
plot(solution.phase.time, solution.phase.control,'-o','LineWidth',1.5);
xlabel('Time',...
'FontWeight','bold');
ylabel('Control',...
'FontWeight','bold');
set(gca,'FontName','Times New Roman',...
'FontSize',15,...
'LineWidth',1.3);
print -dpng moonlander_control.png
continuous function
function phaseout = mlocpContinuous(input)
g = input.auxdata.g;
t = input.phase.time;
h = input.phase.state(:,1);
v = input.phase.state(:,2);
u = input.phase.control(:,1);
dh = v;
dv = -g + u;
phaseout.dynamics = [dh, dv];
phaseout.integrand = u;
end
endpoint function
function output = mlocpEndpoint(input)
J = input.phase.integral;
output.objective = J;
end
仿真结果
状态量:
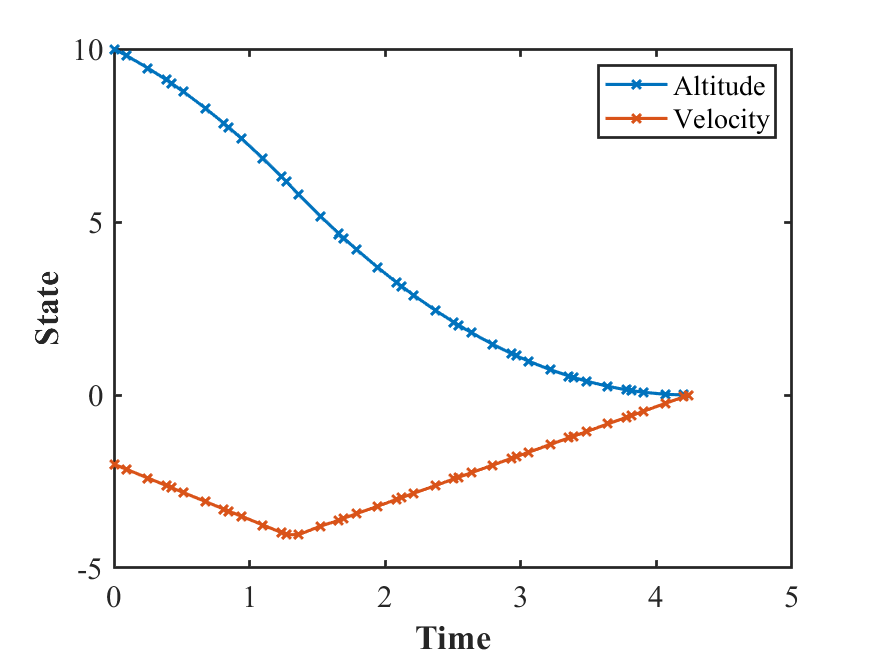
控制量
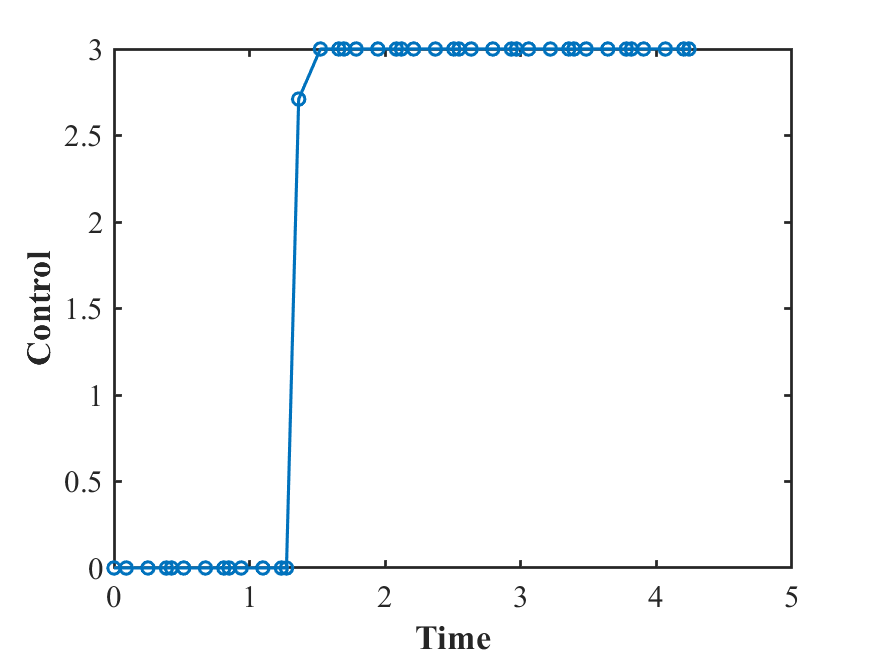
最后
欢迎通过邮箱联系我:lordofdapanji@foxmail.com
来信请注明你的身份,否则恕不回信。