GPOPS-II教程(2): 可复用火箭再入大气层最优轨迹规划问题
问题描述
考虑一类可复用火箭再入大气层最优轨迹规划问题,其动力学方程为
\[\left \{ \begin{aligned} &\dot r = v \sin \gamma, \\ &\dot \theta = \frac{v \cos \gamma \sin \psi}{r \cos \phi}, \\ &\dot \phi = \frac{v \cos \gamma \cos \psi}{r}, \\ &\dot v = - \frac{F_d}{m}-F_g \sin \gamma, \\ &\dot \gamma = \frac{F_l \cos \sigma}{m v} - (\frac{F_g}{v} - \frac{v}{r}) \cos \gamma, \\ &\dot \psi = \frac{F_l \sin \sigma}{m v \cos \gamma} + \frac{v \cos r \sin \psi \tan \phi}{r}, \end{aligned} \right .\]边界条件为
\[\left \{ \begin{array}{lcl} r(0) = 79248 + R_e \ \text{m}\ &,\ &r(t_f) = 79248 + R_e \ \text{m}, \\ \theta(0) = 0 \ \text{deg}\ &,\ & \theta(t_f) = \text{Free}, \\ \phi(0) = 0 \ \text{deg}\ &,\ & \phi(t_f) = \text{Free}, \\ v(0) = 7803 \ \text{m/s}\ &,\ & v(t_f) = 762 \ \text{m/s}, \\ \gamma(0) = -1 \ \text{deg}\ &,\ & \gamma(t_f) = -5 \ \text{deg}, \\ \psi(0) = 90 \ \text{deg}\ &,\ & \psi(t_f) = \text{Free}. \end{array} \right.\]性能指标为
\[J = -\phi(t_f).\]参考文献: [1] Betts J T. Practical methods for optimal control and estimation using nonlinear programming[M]. Society for Industrial and Applied Mathematics, 247-252, 2010.
GPOPS代码
main function
虽然这个最优控制问题很复杂,不过不要着急,心里要有一个顺序,按照顺序一步一步写下去就行。
按照我的习惯,main function一般分成6个步骤,分别是:
- 初始参数设置;
- 边界条件设置;
- 初值猜测;
- 设置GPOPS求解器参数;
- 求解;
- 画图。
那么,一步一步地来写代码吧。
1. 初始参数设置
%% 01.初始参数设置
%-------------------------------------------------------------------------%
%----------------------- 设置问题的求解边界 ------------------------------%
%-------------------------------------------------------------------------%
cft2m = 0.3048;
cft2km = cft2m/1000;
cslug2kg = 14.5939029;
%-------------------------------------%
% Problem Setup %
%-------------------------------------%
auxdata.Re = 20902900*cft2m; % Equatorial Radius of Earth (m)
auxdata.S = 2690*cft2m^2; % Vehicle Reference Area (m^2)
auxdata.cl(1) = -0.2070; % Parameters for lift coefficient
auxdata.cl(2) = 1.6756;
auxdata.cd(1) = 0.0785;
auxdata.cd(2) = -0.3529;
auxdata.cd(3) = 2.0400;
auxdata.b(1) = 0.07854;
auxdata.b(2) = -0.061592;
auxdata.b(3) = 0.00621408;
auxdata.H = 23800*cft2m; % Density Scale Height (m)
auxdata.al(1) = -0.20704;
auxdata.al(2) = 0.029244;
auxdata.rho0 = 0.002378*cslug2kg/cft2m^3;% Sea Level Atmospheric Density (slug/ft^3)
auxdata.mu = 1.4076539e16*cft2m^3; % Earth Gravitational Parameter (ft^^3/s^2)
auxdata.mass = 6309.433*cslug2kg;
% 初始条件
t0 = 0;
alt0 = 260000*cft2m;
rad0 = alt0+auxdata.Re;
lon0 = 0;
lat0 = 0;
speed0 = 25600*cft2m;
fpa0 = -1*pi/180;
azi0 = 90*pi/180;
% 终端条件
altf = 80000*cft2m;
radf = altf+auxdata.Re;
speedf = 2500*cft2m;
fpaf = -5*pi/180;
azif = -90*pi/180;
%----------------------------------------------------%
% 时间、状态和控制量的上界和下界
%----------------------------------------------------%
tfMin = 0; tfMax = 3000;
radMin = auxdata.Re; radMax = rad0;
lonMin = -pi; lonMax = -lonMin;
latMin = -70*pi/180; latMax = -latMin;
speedMin = 10; speedMax = 45000;
fpaMin = -80*pi/180; fpaMax = 80*pi/180;
aziMin = -180*pi/180; aziMax = 180*pi/180;
aoaMin = -90*pi/180; aoaMax = -aoaMin;
bankMin = -90*pi/180; bankMax = 1*pi/180;
2. 边界条件设置
%-------------------------------------------------------------------------%
%------------------------ 将求解边界设置于问题中 -------------------------%
%-------------------------------------------------------------------------%
bounds.phase.initialtime.lower = t0;
bounds.phase.initialtime.upper = t0;
bounds.phase.finaltime.lower = tfMin;
bounds.phase.finaltime.upper = tfMax;
bounds.phase.initialstate.lower = [rad0, lon0, lat0, speed0, fpa0, azi0];
bounds.phase.initialstate.upper = [rad0, lon0, lat0, speed0, fpa0, azi0];
bounds.phase.state.lower = [radMin, lonMin, latMin, speedMin, fpaMin, aziMin];
bounds.phase.state.upper = [radMax, lonMax, latMax, speedMax, fpaMax, aziMax];
bounds.phase.finalstate.lower = [radf, lonMin, latMin, speedf, fpaf, aziMin];
bounds.phase.finalstate.upper = [radf, lonMax, latMax, speedf, fpaf, aziMax];
bounds.phase.control.lower = [aoaMin, bankMin];
bounds.phase.control.upper = [aoaMax, bankMax];
3. 初值猜测
%-------------------------------------------------------------------------%
%------------------------------- 初值猜想 --------------------------------%
%-------------------------------------------------------------------------%
tGuess = [0; 1000];
radGuess = [rad0; radf];
lonGuess = [lon0; lon0+10*pi/180];
latGuess = [lat0; lat0+10*pi/180];
speedGuess = [speed0; speedf];
fpaGuess = [fpa0; fpaf];
aziGuess = [azi0; azif];
aoaGuess = [0; 0];
bankGuess = [0; 0];
guess.phase.state = [radGuess, lonGuess, latGuess, speedGuess, fpaGuess, aziGuess];
guess.phase.control = [aoaGuess, bankGuess];
guess.phase.time = tGuess;
4. 设置GPOPS求解器参数
%-------------------------------------------------------------------------%
%---------------------------- 设置求解器参数 -----------------------------%
%-------------------------------------------------------------------------%
meshphase.colpoints = 4*ones(1,10);
meshphase.fraction = 0.1*ones(1,10);
setup.name = 'Reusable-Launch-Vehicle-Entry-Problem';
setup.functions.continuous = @rlvEntryContinuous;
setup.functions.endpoint = @rlvEntryEndpoint;
setup.auxdata = auxdata;
setup.mesh.phase = meshphase;
setup.bounds = bounds;
setup.guess = guess;
setup.nlp.solver = 'ipopt';
setup.derivatives.supplier = 'sparseCD';
setup.derivatives.derivativelevel = 'second';
setup.scales.method = 'automatic-bounds';
setup.mesh.method = 'hp1';
setup.mesh.tolerance = 1e-6;
setup.mesh.colpointsmin = 4;
setup.mesh.colpointsmax = 16;
5. 求解
%-------------------------------------------------------------------------%
%----------------------- 使用 GPOPS2 求解最优控制问题 --------------------%
%-------------------------------------------------------------------------%
output = gpops2(setup);
solution = output.result.solution;
toc;
time = solution.phase(1).time;
altitude = (solution.phase(1).state(:,1)-auxdata.Re)/1000;
longitude = solution.phase(1).state(:,2)*180/pi;
latitude = solution.phase(1).state(:,3)*180/pi;
speed = solution.phase(1).state(:,4)/1000;
fpa = solution.phase(1).state(:,5)*180/pi;
azimuth = solution.phase(1).state(:,6)*180/pi;
aoa = solution.phase(1).control(:,1)*180/pi;
bank = solution.phase(1).control(:,2)*180/pi;
6. 画图
figure('Color',[1,1,1])
pp = plot(time,altitude,'-o', 'markersize', 7, 'linewidth', 1.5);
xl = xlabel('Time (s)');
yl = ylabel('Altitude (km)');
title('Altitude');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvAltitude.png
figure('Color',[1,1,1])
plot(longitude,latitude,'-o', 'markersize', 7, 'linewidth', 1.5);
xl = xlabel('Longitude (deg)');
yl = ylabel('Latitude (deg)');
title('Longitude and Latitude');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvLonLat.png
figure('Color',[1,1,1])
plot(time,speed,'-o', 'markersize', 7, 'linewidth', 1.5);
xl = xlabel('Time (s)');
yl = ylabel('Speed (km/s)');
title('Speed')
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvSpeed.png
figure('Color',[1,1,1])
plot(time,fpa,'-o', 'markersize', 7, 'linewidth', 1.5);
yl = xlabel('Time (s)');
xl = ylabel('Flight Path Angle (deg)');
title('Flight Path Angle')
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvFlightPathAngle.png
figure('Color',[1,1,1])
plot(time,azimuth,'-o', 'markersize', 7, 'linewidth', 1.5);
yl = xlabel('Time (s)');
xl = ylabel('Azimuth Angle (deg)');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvAzimuthAngle.png
figure('Color',[1,1,1])
plot(time,aoa,'-o', 'markersize', 7, 'linewidth', 1.5);
yl = xlabel('Time (s)');
xl = ylabel('Angle of Attack (deg)');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'YTick',[16.5 17 17.5],'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvAngleofAttack.png
figure('Color',[1,1,1])
plot(time,bank,'-o', 'markersize', 7, 'linewidth', 1.5);
yl = xlabel('Time (s)');
xl = ylabel('Bank Angle (deg)');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvBankAngle.png
continuous function
写这部分代码的时候分成三步来写。
第一步,把所有要用的变量全部导入进来。
function phaseout = rlvEntryContinuous(input)
rad = input.phase.state(:,1);
lon = input.phase.state(:,2);
lat = input.phase.state(:,3);
speed = input.phase.state(:,4);
fpa = input.phase.state(:,5);
azimuth = input.phase.state(:,6);
aoa = input.phase.control(:,1);
bank = input.phase.control(:,2);
cd0 = input.auxdata.cd(1);
cd1 = input.auxdata.cd(2);
cd2 = input.auxdata.cd(3);
cl0 = input.auxdata.cl(1);
cl1 = input.auxdata.cl(2);
mu = input.auxdata.mu;
rho0 = input.auxdata.rho0;
H = input.auxdata.H;
S = input.auxdata.S;
mass = input.auxdata.mass;
altitude = rad - input.auxdata.Re;
第二步,计算在求解动力学方程时会用到的变量。
CD = cd0+cd1*aoa+cd2*aoa.^2;
rho = rho0*exp(-altitude/H);
CL = cl0+cl1*aoa;
gravity = mu./rad.^2;
dynamic_pressure = 0.5*rho.*speed.^2;
D = dynamic_pressure.*S.*CD./mass;
L = dynamic_pressure.*S.*CL./mass;
slon = sin(lon);
clon = cos(lon);
slat = sin(lat);
clat = cos(lat);
tlat = tan(lat);
sfpa = sin(fpa);
cfpa = cos(fpa);
sazi = sin(azimuth);
cazi = cos(azimuth);
cbank = cos(bank);
sbank = sin(bank);
第三步,根据动力学方程写出代码。
重新复习一下动力学方程,为
\[\left \{ \begin{aligned} &\dot r = v \sin \gamma, \\ &\dot \theta = \frac{v \cos \gamma \sin \psi}{r \cos \phi}, \\ &\dot \phi = \frac{v \cos \gamma \cos \psi}{r}, \\ &\dot v = - \frac{F_d}{m}-F_g \sin \gamma, \\ &\dot \gamma = \frac{F_l \cos \sigma}{m v} - (\frac{F_g}{v} - \frac{v}{r}) \cos \gamma, \\ &\dot \psi = \frac{F_l \sin \sigma}{m v \cos \gamma} + \frac{v \cos r \sin \psi \tan \phi}{r}, \end{aligned} \right .\]根据动力学方程,就可以对应地写出,代码如下。
raddot = speed.*sfpa;
londot = speed.*cfpa.*sazi./(rad.*clat);
latdot = speed.*cfpa.*cazi./rad;
speeddot = -D-gravity.*sfpa;
fpadot = (L.*cbank-cfpa.*(gravity-speed.^2./rad))./speed;
azidot = (L.*sbank./cfpa + speed.^2.*cfpa.*sazi.*tlat./rad)./speed;
phaseout.dynamics = [raddot, londot, latdot, speeddot, fpadot, azidot];
end
endpoint function
endpoint function按照性能指标函数写即可,性能指标为
那么,代码如下。
% ----------------------------------------------------------------------- %
% ------------------------ BEGIN: rlvEntryEndpoint.m -------------------- %
% ----------------------------------------------------------------------- %
function output = rlvEntryEndpoint(input)
latf = input.phase.finalstate(3);
output.objective = -latf;
end
% ----------------------------------------------------------------------- %
% ------------------------- END: rlvEntryEndpoint.m --------------------- %
% ----------------------------------------------------------------------- %
完整代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 功能描述:可复用火箭再入大气层最优轨迹规划问题
% 文件名解释:mainReentry.m 中,main 代表 主函数,
% Re-entry 代表 再入航天器
% 作者:Lei Lie
% 时间:2024/06/24
% 版本:1.0
% - 完成了代码框架的初始搭建
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
clear;
close all;
tic;
%% 01.初始参数设置
%-------------------------------------------------------------------------%
%----------------------- 设置问题的求解边界 ------------------------------%
%-------------------------------------------------------------------------%
cft2m = 0.3048;
cft2km = cft2m/1000;
cslug2kg = 14.5939029;
%-------------------------------------%
% Problem Setup %
%-------------------------------------%
auxdata.Re = 20902900*cft2m; % Equatorial Radius of Earth (m)
auxdata.S = 2690*cft2m^2; % Vehicle Reference Area (m^2)
auxdata.cl(1) = -0.2070; % Parameters for lift coefficient
auxdata.cl(2) = 1.6756;
auxdata.cd(1) = 0.0785;
auxdata.cd(2) = -0.3529;
auxdata.cd(3) = 2.0400;
auxdata.b(1) = 0.07854;
auxdata.b(2) = -0.061592;
auxdata.b(3) = 0.00621408;
auxdata.H = 23800*cft2m; % Density Scale Height (m)
auxdata.al(1) = -0.20704;
auxdata.al(2) = 0.029244;
auxdata.rho0 = 0.002378*cslug2kg/cft2m^3;% Sea Level Atmospheric Density (slug/ft^3)
auxdata.mu = 1.4076539e16*cft2m^3; % Earth Gravitational Parameter (ft^^3/s^2)
auxdata.mass = 6309.433*cslug2kg;
% 初始条件
t0 = 0;
alt0 = 260000*cft2m;
rad0 = alt0+auxdata.Re;
lon0 = 0;
lat0 = 0;
speed0 = 25600*cft2m;
fpa0 = -1*pi/180;
azi0 = 90*pi/180;
% 终端条件
altf = 80000*cft2m;
radf = altf+auxdata.Re;
speedf = 2500*cft2m;
fpaf = -5*pi/180;
azif = -90*pi/180;
%----------------------------------------------------%
% 时间、状态和控制量的上界和下界
%----------------------------------------------------%
tfMin = 0; tfMax = 3000;
radMin = auxdata.Re; radMax = rad0;
lonMin = -pi; lonMax = -lonMin;
latMin = -70*pi/180; latMax = -latMin;
speedMin = 10; speedMax = 45000;
fpaMin = -80*pi/180; fpaMax = 80*pi/180;
aziMin = -180*pi/180; aziMax = 180*pi/180;
aoaMin = -90*pi/180; aoaMax = -aoaMin;
bankMin = -90*pi/180; bankMax = 1*pi/180;
%% 02.边界条件设置
%-------------------------------------------------------------------------%
%------------------------ 将求解边界设置于问题中 -------------------------%
%-------------------------------------------------------------------------%
bounds.phase.initialtime.lower = t0;
bounds.phase.initialtime.upper = t0;
bounds.phase.finaltime.lower = tfMin;
bounds.phase.finaltime.upper = tfMax;
bounds.phase.initialstate.lower = [rad0, lon0, lat0, speed0, fpa0, azi0];
bounds.phase.initialstate.upper = [rad0, lon0, lat0, speed0, fpa0, azi0];
bounds.phase.state.lower = [radMin, lonMin, latMin, speedMin, fpaMin, aziMin];
bounds.phase.state.upper = [radMax, lonMax, latMax, speedMax, fpaMax, aziMax];
bounds.phase.finalstate.lower = [radf, lonMin, latMin, speedf, fpaf, aziMin];
bounds.phase.finalstate.upper = [radf, lonMax, latMax, speedf, fpaf, aziMax];
bounds.phase.control.lower = [aoaMin, bankMin];
bounds.phase.control.upper = [aoaMax, bankMax];
%% 03.初值猜测
%-------------------------------------------------------------------------%
%------------------------------- 初值猜想 --------------------------------%
%-------------------------------------------------------------------------%
tGuess = [0; 1000];
radGuess = [rad0; radf];
lonGuess = [lon0; lon0+10*pi/180];
latGuess = [lat0; lat0+10*pi/180];
speedGuess = [speed0; speedf];
fpaGuess = [fpa0; fpaf];
aziGuess = [azi0; azif];
aoaGuess = [0; 0];
bankGuess = [0; 0];
guess.phase.state = [radGuess, lonGuess, latGuess, speedGuess, fpaGuess, aziGuess];
guess.phase.control = [aoaGuess, bankGuess];
guess.phase.time = tGuess;
%% 04.设置GPOPS求解器参数
%-------------------------------------------------------------------------%
%---------------------------- 设置求解器参数 -----------------------------%
%-------------------------------------------------------------------------%
meshphase.colpoints = 4*ones(1,10);
meshphase.fraction = 0.1*ones(1,10);
setup.name = 'Reusable-Launch-Vehicle-Entry-Problem';
setup.functions.continuous = @rlvEntryContinuous;
setup.functions.endpoint = @rlvEntryEndpoint;
setup.auxdata = auxdata;
setup.mesh.phase = meshphase;
setup.bounds = bounds;
setup.guess = guess;
setup.nlp.solver = 'ipopt';
setup.derivatives.supplier = 'sparseCD';
setup.derivatives.derivativelevel = 'second';
setup.scales.method = 'automatic-bounds';
setup.mesh.method = 'hp1';
setup.mesh.tolerance = 1e-6;
setup.mesh.colpointsmin = 4;
setup.mesh.colpointsmax = 16;
%% 05.求解
%-------------------------------------------------------------------------%
%----------------------- 使用 GPOPS2 求解最优控制问题 --------------------%
%-------------------------------------------------------------------------%
output = gpops2(setup);
solution = output.result.solution;
toc;
time = solution.phase(1).time;
altitude = (solution.phase(1).state(:,1)-auxdata.Re)/1000;
longitude = solution.phase(1).state(:,2)*180/pi;
latitude = solution.phase(1).state(:,3)*180/pi;
speed = solution.phase(1).state(:,4)/1000;
fpa = solution.phase(1).state(:,5)*180/pi;
azimuth = solution.phase(1).state(:,6)*180/pi;
aoa = solution.phase(1).control(:,1)*180/pi;
bank = solution.phase(1).control(:,2)*180/pi;
%% 06.画图
figure('Color',[1,1,1])
pp = plot(time,altitude,'-o', 'markersize', 7, 'linewidth', 1.5);
xl = xlabel('Time (s)');
yl = ylabel('Altitude (km)');
title('Altitude');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvAltitude.png
figure('Color',[1,1,1])
plot(longitude,latitude,'-o', 'markersize', 7, 'linewidth', 1.5);
xl = xlabel('Longitude (deg)');
yl = ylabel('Latitude (deg)');
title('Longitude and Latitude');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvLonLat.png
figure('Color',[1,1,1])
plot(time,speed,'-o', 'markersize', 7, 'linewidth', 1.5);
xl = xlabel('Time (s)');
yl = ylabel('Speed (km/s)');
title('Speed')
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvSpeed.png
figure('Color',[1,1,1])
plot(time,fpa,'-o', 'markersize', 7, 'linewidth', 1.5);
yl = xlabel('Time (s)');
xl = ylabel('Flight Path Angle (deg)');
title('Flight Path Angle')
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvFlightPathAngle.png
figure('Color',[1,1,1])
plot(time,azimuth,'-o', 'markersize', 7, 'linewidth', 1.5);
yl = xlabel('Time (s)');
xl = ylabel('Azimuth Angle (deg)');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvAzimuthAngle.png
figure('Color',[1,1,1])
plot(time,aoa,'-o', 'markersize', 7, 'linewidth', 1.5);
yl = xlabel('Time (s)');
xl = ylabel('Angle of Attack (deg)');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'YTick',[16.5 17 17.5],'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvAngleofAttack.png
figure('Color',[1,1,1])
plot(time,bank,'-o', 'markersize', 7, 'linewidth', 1.5);
yl = xlabel('Time (s)');
xl = ylabel('Bank Angle (deg)');
set(xl,'FontSize',18);
set(yl,'FontSize',18);
set(gca,'FontSize',16,'FontName','Times New Roman');
set(pp,'LineWidth',1.25);
print -dpng rlvBankAngle.png
%% 函数模块部分
% ----------------------------------------------------------------------- %
% ----------------------- BEGIN: rlvEntryContinuous.m ------------------- %
% ----------------------------------------------------------------------- %
function phaseout = rlvEntryContinuous(input)
rad = input.phase.state(:,1);
lon = input.phase.state(:,2);
lat = input.phase.state(:,3);
speed = input.phase.state(:,4);
fpa = input.phase.state(:,5);
azimuth = input.phase.state(:,6);
aoa = input.phase.control(:,1);
bank = input.phase.control(:,2);
cd0 = input.auxdata.cd(1);
cd1 = input.auxdata.cd(2);
cd2 = input.auxdata.cd(3);
cl0 = input.auxdata.cl(1);
cl1 = input.auxdata.cl(2);
mu = input.auxdata.mu;
rho0 = input.auxdata.rho0;
H = input.auxdata.H;
S = input.auxdata.S;
mass = input.auxdata.mass;
altitude = rad - input.auxdata.Re;
CD = cd0+cd1*aoa+cd2*aoa.^2;
rho = rho0*exp(-altitude/H);
CL = cl0+cl1*aoa;
gravity = mu./rad.^2;
dynamic_pressure = 0.5*rho.*speed.^2;
D = dynamic_pressure.*S.*CD./mass;
L = dynamic_pressure.*S.*CL./mass;
slon = sin(lon);
clon = cos(lon);
slat = sin(lat);
clat = cos(lat);
tlat = tan(lat);
sfpa = sin(fpa);
cfpa = cos(fpa);
sazi = sin(azimuth);
cazi = cos(azimuth);
cbank = cos(bank);
sbank = sin(bank);
raddot = speed.*sfpa;
londot = speed.*cfpa.*sazi./(rad.*clat);
latdot = speed.*cfpa.*cazi./rad;
speeddot = -D-gravity.*sfpa;
fpadot = (L.*cbank-cfpa.*(gravity-speed.^2./rad))./speed;
azidot = (L.*sbank./cfpa + speed.^2.*cfpa.*sazi.*tlat./rad)./speed;
phaseout.dynamics = [raddot, londot, latdot, speeddot, fpadot, azidot];
end
% ----------------------------------------------------------------------- %
% ------------------------ END: rlvEntryContinuous.m -------------------- %
% ----------------------------------------------------------------------- %
% ----------------------------------------------------------------------- %
% ------------------------ BEGIN: rlvEntryEndpoint.m -------------------- %
% ----------------------------------------------------------------------- %
function output = rlvEntryEndpoint(input)
latf = input.phase.finalstate(3);
output.objective = -latf;
end
% ----------------------------------------------------------------------- %
% ------------------------- END: rlvEntryEndpoint.m --------------------- %
% ----------------------------------------------------------------------- %
代码仿真结果
高度:
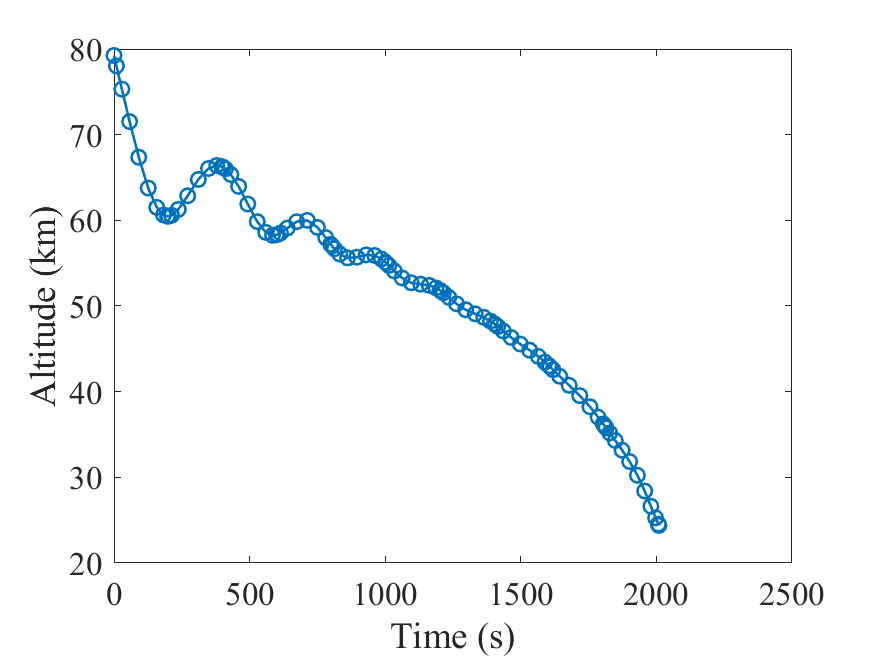
速度:
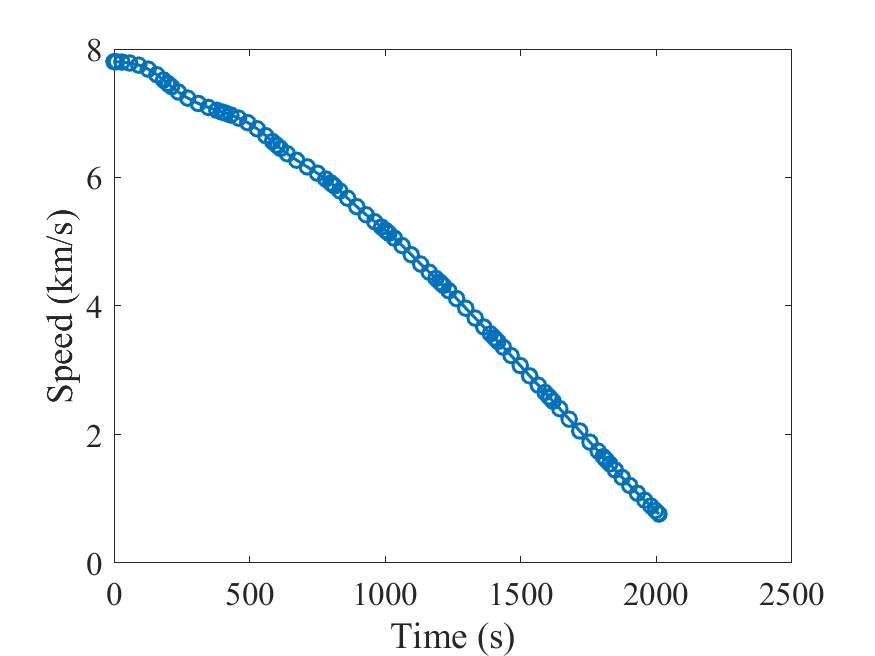
经纬度:
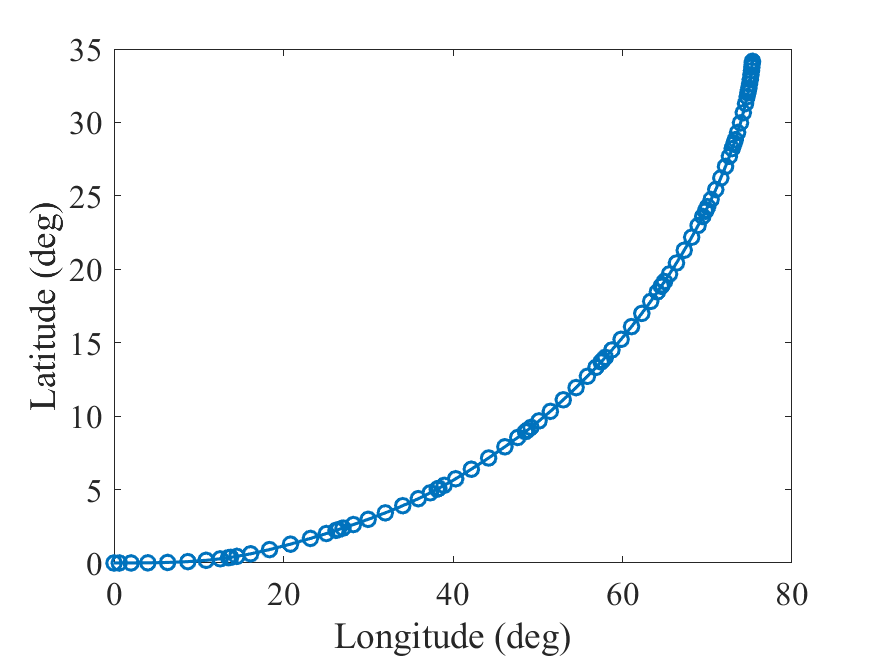
飞行路径角度:
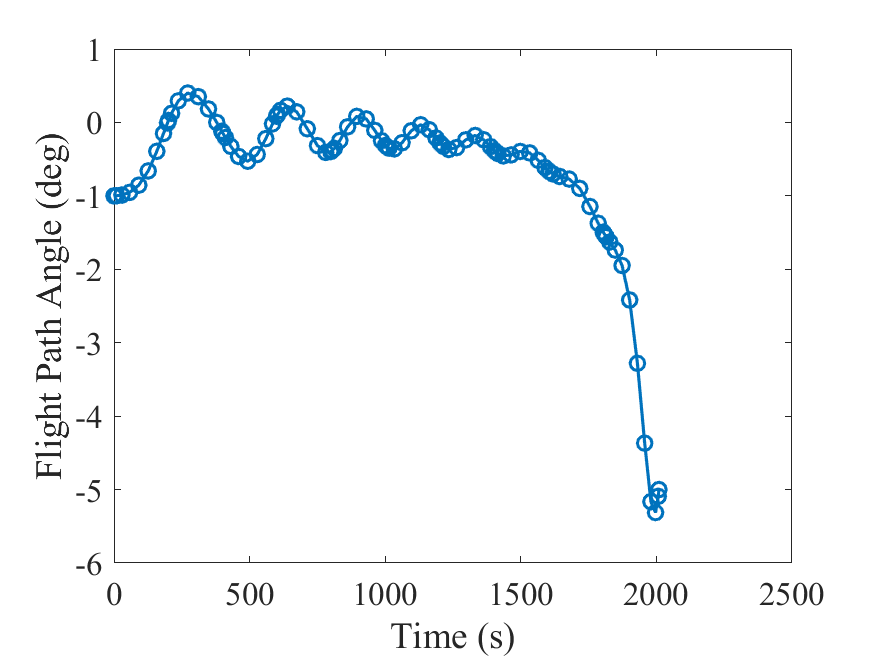
攻角:
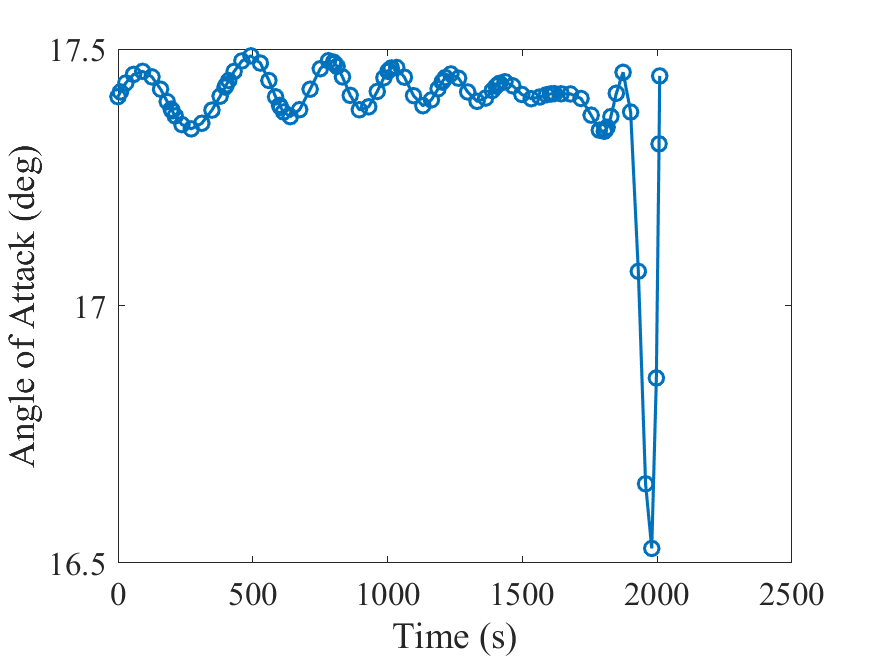
倾斜角:
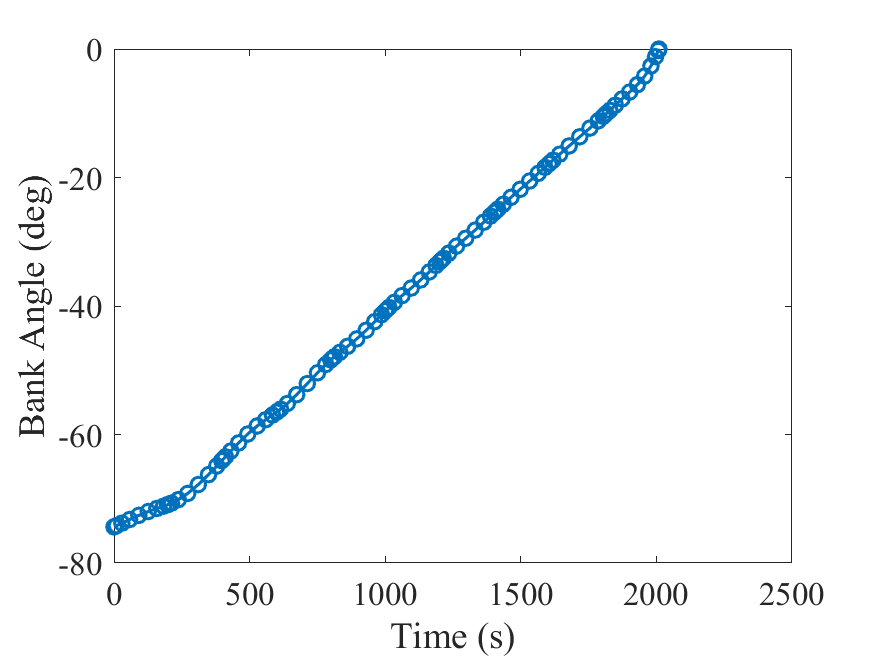
最后
关于可复用火箭再入大气层的最优轨迹规划问题,没有写得很详细每个参数为什么这么取的原因,是我觉得现在大家都大概率不需要解决这个问题。所以诸如攻角、仰角、迎角之类的变量不去解释为什么要这么写。
只是希望通过这样一系列的例子告诉大家GPOPS-II应该怎么使用的思路。
- 动力学方程应该怎么写?
- 性能指标应该怎么写?
- 约束应该怎么写?
- 猜测应该怎么写?
- 画图怎么画?
要被解决的问题是无限的,只有掌握了方法论,才能一法通时万法通。
欢迎通过邮箱联系我:lordofdapanji@foxmail.com
来信请注明你的身份,否则恕不回信。