GPOPS-II教程(1): 语法和一个最优控制问题案例

2024-06-20

一、写在前面

很多同学都在用GPOPS-II做轨迹优化，我在后台里也看见了许许多多的问题来问我。所以想写一个教程，把一些GPOPS-II的例子讲讲，从这些例子中教会如何使用GPOPS-II。

这个教程会分成几个部分，前面几个部分会讲解GPOPS-II的官方案例。通过讲解这些官方案例，说明GPOPS-II的语法应该怎么写，会有什么样的trips。

然后会给出一个总结，总结内容是关于使用GPOPS-II遇见不同问题时，有什么样共性的解决方法，以及各类针对性的解决方法。最后行有余力，给出一个如何调试BUG的教程。

参考文章：

二、GPOPS-II结构

GPOPS-II主要由3部分组成：

主函数 main function：用于设置求解问题的各类初始参数，配置GPOPS参数，进行计算并得出结果。
连续函数 continuous function：用于表示求解问题的动力学关系，计算每个阶段的被积函数和路径约束。
端点函数 endpoint function：用于定义各个阶段初始点和终端点的值，计算求解问题的成本（性能指标）。

在 main function里，要指定求解问题的上下限，以一个阶段（phase）为例，一般包括如下几类：

边界条件 bounds
- 初始时间、终端时间
- 初始状态、终端状态
- 控制量
- 积分量
初值猜测 guess
- 初始时间、终端时间
- 初始状态、终端状态
- 控制量
- 积分量
路径约束 path
事件约束 event
静态参数 auxdata

上述变量，统一被 setup 纳入结构体变量之中。可写作

ouput = gpops2(setup)

其中，其中setup是一个用户定义的结构体变量，该结构体变量包含有关要解决的最优控制问题的所有信息；output是一个结构体变量，其包含通过解决最优控制的问题而获得的信息。下面对setup进行详细解释。

2.1 setup的语法

setup包含必填字段和可选字段。setup中的必填字段如下：

name：不带空格的字符串，对要求解问题的描述；
function：包含连续函数continuous function和端点函数endpoint function的结构体；
bounds：包含变量和约束的上下限信息的结构体；
guess：包含对问题中的时间、状态、控制、积分和静态参数的猜测的结构体。

可选字段如下：

auxdata：辅助数据的结构体，这样就可以不使用全局变量而使用auxdata.args来传递求解问题时所需要用到的部分常量。（args代表任意需要命名的参数，即参数arguments的缩写，无实际意义。）
derivatives：指定 NLP 求解器所使用的导数近似和 NLP 求解器所使用的导数阶次（first或second）的结构。衍生字段包含
- derivatives.supplier：NLP 求解器所使用的导数近似，可选值为sparseFD, sparseBD, sparseCD，默认值为 sparseFD。
- derivatives.derivativelevel：NLP 求解器使用的导数阶次，可选值为 first, second，默认值为 first。
- derivatives.dependencies：NLP 求解器的依赖关系，可选值为 full, sparse, spareseNaN，默认值为 sparseNaN。
scales：求解问题时要使用的尺度类型，可选项为none和automatic-bounds，默认值为none。
mesh：求解问题的网格细化方法，包括网格细化类型、精度公差及初始网格。衍生字段包含
- mesh.method：网格细化方法，可选值为 hp, hp1，默认值为hp1。
- mesh.options.tolerance：网格要求的精度容差，为0到1之间的正数，默认值为$10$。
- mesh.options.maxiteration：网格细化最大的迭代次数，为非负整数，默认值为$10^{-3}$。
- mesh.colpointsmin：网格间隔中配置点最小数量，默认值为$3$。
- mesh.colpointsmax：网格间隔中配置点最大数量，默认值为$10$。
- mesh.phase.fraction：每个阶段的网络间隔，是一个0到1的缩放区间，N个间隔，行向量加起来等于1，默认值为0.1*ones(1,10)。
- mesh.phase.colpoints：每个阶段的配置点，也是行向量，默认值为4*ones(1,10)。
nlp：要使用的 NLP 求解器类型结构体，可选字段包含
- nlp.solver：求解器类型，可选值为 snopt, ipopt。
- nlp.ipoptoptions
  - nlp.ipoptoptions.linear_solver：mumps or ma57。
  - nlp.ipoptoptions.tolerance：默认值 $10^{-7}$。
  - nlp.ipoptoptions.maxiterations：默认值为 $2000$。
- nlp.snoptoptions
  - nlp.snoptoptions.tolerance：默认值为 $10^{−6}$。
  - nlp.snoptoptions.maxiterations：默认 $2000$。

2.2 function的语法

指定连续函数和端点函数的函数句柄，代码为

setup.functions.continuous = @continuousfun
setup.functions.endpoint   = @endpointfun

2.2.1 setup.functions.continuousfun

格式为

\[\rm function\ output = continuousfun(input)\]

输入包括

input.phase(p).time：时间。
input.phase(p).state：状态量。
input.phase(p).control：控制量。
input.phase(p).parameter：静态参数量。

输出是一个长度为 $P$ 的结构向量，包括

output.dynamics：微分状态。
output.path：路径约束。
output.integrand：积分。

2.2.2 setup.functions.endpoint

格式为

\[\rm function\ output = endpointfun(input)\]

输入包括

input.phase(p).initialtime：阶段p的起始时间。
input.phase(p).finaltime：阶段p的起始时间。
input.phase(p).initialstate：阶段p的起始状态。
input.phase(p).finalstate：阶段p的终止状态。
input.phase(p).integral：阶段p的积分。
input.parameter：阶段p的静态参数。

输出包括两个成员

output.objective：标量，目标函数。
output.eventgroup。

2.3 bounds的语法

此处参考GPOPS-II教程。

包括3个成员：

bounds.phase: 指定了时间、状态、控制、路径约束和每个阶段的积分的界限。
- phase.initialtime.lower: 起始时间的下界。
- phase.initialtime.upper: 起始时间的上界。
- phase(p).finaltime.lower: 终止时间的下界。
- phase(p).finaltime.upper: 终止时间的上界。
- phase(p).initialstate.lower: 初始状态的下界。
- phase(p).initialstate.upper: 初始状态的上界。
- phase(p).state.lower: 每个阶段状态的下界。
- phase(p).state.upper: 每个阶段状态的上界。
- phase(p).finalstate.lower: 终止状态的下界。
- phase(p).finalstate.upper: 终止状态的上界。
- phase(p).control.lower: 每个阶段控制的下界。
- phase(p).control.upper: 每个阶段控制的上界。
- phase(p).path.lower: 每个阶段路径约束的下界。
- phase(p).path.upper: 每个阶段路径约束的上界。
- phase(p).integral.lower: 每个阶段积分的下界。
- phase(p).integral.upper: 每个阶段积分的上界。
- phase(p).duration.lower: 每个阶段时间的下界。
- phase(p).duration.upper: 每个阶段时间的上界。
bounds.parameters: 包含问题中静态参数的下界和上界。
bounds.eventgroup: 长度为G的结构数组，其中G是问题中事件组的数量。

setup.guess

guess结构体里面的值代表了整个求解过程的初始值

guess.phase(p).time: 阶段p的时间猜测。
guess.phase(p).state: 阶段p的状态量猜测。
guess.phase(p).control: 阶段p的控制量猜测。
guess.phase(p).integral: 阶段p的积分量猜测。

output

gpops2的输出包括

result
- result.solution：最优的时间、状态和控制以及静态参数。
  - solution.phase(p).time：时间。
  - solution.phase(p).state：状态量。
  - solution.phase(p).control：控制量。
  - solution.parameter：静态参数。
- result.objective：最优值。
- result.setup：问题设置。
- result.nextsetup。
meshhistory：对每个求解NLP的网格进行求解和误差估计。
meshiterations：迭代次数。

上述内容参考自文章GPOPS-II教程，作者kunpeng，遵循CC BY 4.0协议。

三、例题

上面是GPOPS-II的语法部分，了解了GPOPS-II的语法之后，需要例题来帮助理解GPOPS-II的用法。这篇教程里针对一个典型最优控制问题讲解，通过这个理解希望能够让大家明白GPOPS-II中，main function、continuous functioin、endpoint function怎么用。

3.1 问题描述

求解最优控制问题——有约束的停车能耗最优问题

初始时刻车辆位置为$x_1(0)=-2$，速度为$x_2(0)=1$，状态方程为

\[\left\{\begin{matrix} \begin{aligned} \dot x_1(t) &= x_2(t) \\ \dot x_2(t) &= u(t) \end{aligned} \end{matrix}\right. \tag{1}\]

容许控制为

\[\left | u \right | \le M_1 =1.5 \tag{2}\]

终止条件为

\[x_1(t_f)=0,\ x_2(t_f)=0,\ t_f=2 \tag{3}\]

要最小化的性能指标为总能耗，其表达式为

\[J(u)=\int_{t_0}^{t_f}\frac{1}{2}u^2(t)\mathrm dt \tag{4}\]

3.2 代码部分

3.2.1 `main function`

一般会从main function开始写起。

3.2.1.1 初始参数设置

注意到状态初值为$x_1(0)=-2$、$x_2(0)=1$，终止条件里有$t_f=2$，控制约束为$| u | \le M_1 =1.5$。这些都是写代码时首先要加上的初始边界参数，也就是bounds，那么根据式$(2)$、$(3)$和初始条件，给出如下代码：

% 设置时间
t0 = 0;
tf = 2;
% 设置状态量初值
x10 = -2;
x20 = 1;
% 设置控制量边界条件
uMin  = -1.5;
uMax  = 1.5;
% 设置状态量边界条件
x1Min = -5;
x1Max = 5;
x2Min = -5;
x2Max = 5;

注意，最后4行代码

x1Min = -5;
x1Max = 5;
x2Min = -5;
x2Max = 5;

是按照自己的经验给出的值，不一定非要是这个数值。

3.2.1.2 边界条件设置

下面开始设置边界条件，给出代码如下。

ounds.phase.initialtime.lower  = t0;
bounds.phase.initialtime.upper  = t0;
bounds.phase.finaltime.lower    = tf; 
bounds.phase.finaltime.upper    = tf;
bounds.phase.initialstate.lower = [x10 x20]; 
bounds.phase.initialstate.upper = [x10 x20];
bounds.phase.state.lower        = [x1Min x2Min]; 
bounds.phase.state.upper        = [x1Max x2Max];
bounds.phase.finalstate.lower   = [0 0];
bounds.phase.finalstate.upper   = [0 0];
bounds.phase.control.lower      = uMin; 
bounds.phase.control.upper      = uMax;
bounds.phase.integral.lower     = 0; 
bounds.phase.integral.upper     = 10000;

上述代码的意义在上一章全部说明过，这里就不再赘述，只要根据问题的要求就能很自然地写出边界条件。

3.2.1.3 初值猜测

初值猜测的代码如下。

guess.phase.time     = [t0; tf]; 
guess.phase.state    = [[x10 x20];[0 0]];
guess.phase.control  = [1; uMin];
guess.phase.integral = 100;

写初值猜测的代码时，要注意符号。这里是加的是分号;。

以guess.phase.time = [t0; tf]; 为例，t0是初始时间的猜测值，tf是终端是时间的猜测值，用分号;隔开。其余行的代码同理。

多讲一句，有的同学可能看见第2行代码guess.phase.state = [[x10 x20];[0 0]];很迷糊，因为这里有2个变量。要注意，这个题目里是有2个状态量，$x_1$和$x_2$。所以在写初值猜测guess.phase.state时，也要写成2维变量。[x10 x20]为初始状态的猜测值，[0 0]为终端状态的猜测值。

很多同学问我这里的初值猜测是怎么给出的。

我的回答是只能凭经验给出。

给初值有的时候需要一些运气，给得好，就算得准。

另外，因为该问题只有一个阶段，所以phase为默认值，没有给它设置数值。

3.2.1.4 设置GPOPS-II求解器参数

按照上一章的内容，设置GPOPS-II求解器参数，一般用setup作变量名称。代码如下。

setup.name = 'Vehicle-Stopping-OCP';
setup.functions.continuous  = @vsopcContinuous;
setup.functions.endpoint   	= @vsopcEndpoint;
setup.bounds                = bounds;
setup.guess                 = guess;
setup.nlp.solver            = 'snopt';
setup.derivatives.supplier  = 'sparseCD';
setup.derivatives.derivativelevel = 'second';
setup.mesh.method           = 'hp1';
setup.mesh.tolerance        = 1e-6;
setup.mesh.maxiteration     = 45;
setup.mesh.colpointsmax     = 4;
setup.mesh.colpointsmin     = 10;
setup.mesh.phase.fraction   = 0.1*ones(1,10);
setup.mesh.phase.colpoints  = 4*ones(1,10);
setup.method = 'RPMintegration';

上述代码已在前述章节中讲过，不再赘述。如果同学们在解决自己的问题时，发现求解效果不好的话，可以根据每个变量的选项选择更加合适的选项，优化求解效果。

3.2.1.5 求解

求解代码很简单，代码如下。

output = gpops2(setup);
solution = output.result.solution;

第1行代码是用GPOPS-II进行求解。可不能小看这短短1行代码，它背后的工作是很多很多很多的，GPOPS-II里围绕这个函数做了大量工作，有很多没有显现的函数都是为了GPOPS-II能够正常求解。

第2行代码是获得GPOPS-II求解结果。获得求解结果后，可以开始数据处理了。一般而言，数据处理的方式就是数据可视化（画图）、数据保存、数据分析。

3.2.1.6 画图

这里只给出画图的代码。数据保存和数据分析的代码按需自拟。

figure('Color',[1,1,1]);
plot(solution.phase.time(:,1),solution.phase.state(:,1),'-','LineWidth',1.5);hold on;
plot(solution.phase.time(:,1),solution.phase.state(:,2),'-.','LineWidth',1.5);
plot(solution.phase.time(:,1),solution.phase.control(:,1),'--','LineWidth',1.5);
axis([0 2 -2.5 2]);
xlabel('Time',...
       'FontWeight','bold');
ylabel('States',...
       'FontWeight','bold');
legend('Pos','Vel','Acc',...
       'LineWidth',1,...
       'EdgeColor',[1,1,1],...
       'Orientation','horizontal',...
       'Position',[0.5,0.93,0.40,0.055]);
set(gca,'FontName','Times New Roman',...
        'FontSize',15,...
        'LineWidth',1.3);
print -dpng Result.png

3.2.2 `continuous function`

这个部分是问题的动力学方程，防止大家忘记例题的动力学方程是什么样子，在这里再写一遍式$(1)$，公式如下。

\[\left\{\begin{matrix} \begin{aligned} \dot x_1(t) &= x_2(t) \\ \dot x_2(t) &= u(t) \end{aligned} \end{matrix}\right.\]

根据动力学方程，写出对应的continuous function，代码如下。

function phaseout = vsopcContinuous(input)
    t  = input.phase.time;
    x2  = input.phase.state(:,2);
    u   = input.phase.control(:,1);
    
    dx1 = x2;
    dx2 = u;
    
    phaseout.dynamics = [dx1, dx2];
    phaseout.integrand = 0.5*u.^2;
end

dx1=x2和dx2=u就是动力学方程。

phaseout.integrand = 0.5*u.^2;是性能指标的积分项。同样，再复习一遍该问题的性能指标形式，公式如下。

\[J(u)=\int_{t_0}^{t_f}\frac{1}{2}u^2(t)\text{d}t\]

代码和公式是相互对应的。

3.2.3 `endpoint function`

这个部分是问题的性能指标函数，即式$(4)$。可以看出，这个问题的性能指标是积分项，所以代码可以像下面这么写：

function output = vsopcEndpoint(input)
    J  = input.phase.integral;
    output.objective = J;
end

3.3 结果分析

根据前述代码，可以得到如下图所示结果。

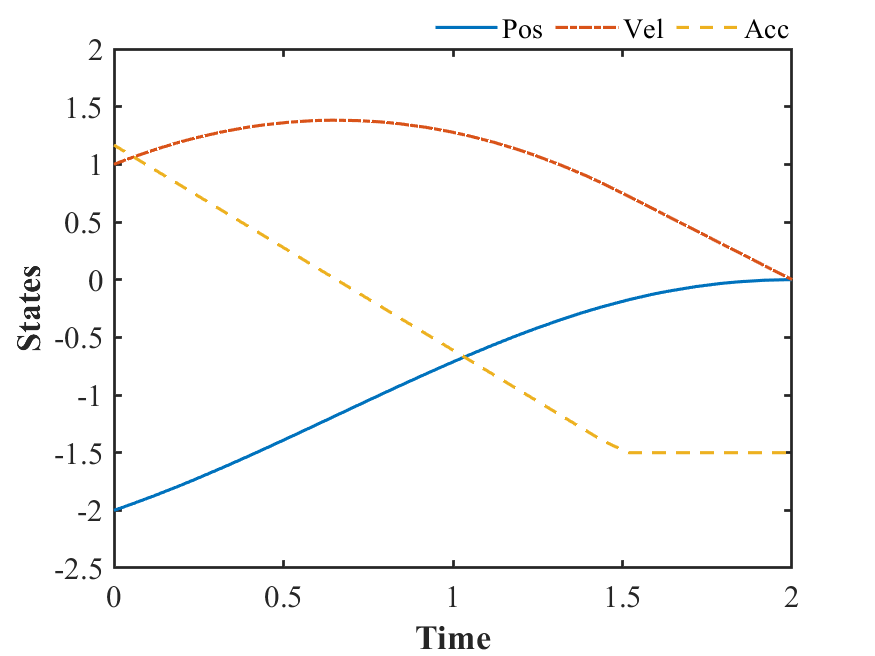
Result

3.4 完整代码

这里给出完整代码。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 功能描述：最优控制问题
% 文件名解释：main_Vehicle_Stopping_OCP.m 中，main 代表 主函数
%             Vehcle_Stopping 代表 停车能耗问题
%			  OCP 代表 最优控制问题.
% 作者：Lei Lie
% 时间：2024/06/21
% 版本：1.0
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;clear;close all;
tic;
%% 01.初始参数设置
%-------------------------------------------------------------------------%
%----------------------- 设置问题的求解边界 ------------------------------%
%-------------------------------------------------------------------------%
% 设置时间
t0 = 0;
tf = 2;
% 设置状态量初值
x10 = -2;
x20 = 1;
% 设置状态量边界条件
x1Min = -5;
x1Max = 5;
x2Min = -5;
x2Max = 5;
% 设置控制量边界条件
uMin  = -1.5;
uMax  = 1.5;

%% 02.边界条件设置
%-------------------------------------------------------------------------%
%------------------------ 将求解边界设置于问题中 -------------------------%
%-------------------------------------------------------------------------%
bounds.phase.initialtime.lower  = t0; 
bounds.phase.initialtime.upper  = t0;
bounds.phase.finaltime.lower    = tf; 
bounds.phase.finaltime.upper    = tf;
bounds.phase.initialstate.lower = [x10 x20]; 
bounds.phase.initialstate.upper = [x10 x20];
bounds.phase.state.lower        = [x1Min x2Min]; 
bounds.phase.state.upper        = [x1Max x2Max];
bounds.phase.finalstate.lower   = [0 0];
bounds.phase.finalstate.upper   = [0 0];
bounds.phase.control.lower      = uMin; 
bounds.phase.control.upper      = uMax;
bounds.phase.integral.lower     = 0; 
bounds.phase.integral.upper     = 10000;

%% 03.初值猜测
%-------------------------------------------------------------------------%
%------------------------------- 初值猜想 --------------------------------%
%-------------------------------------------------------------------------%
guess.phase.time     = [t0; tf]; 
guess.phase.state    = [[x10 x20];[0 0]];
guess.phase.control  = [1; uMin];
guess.phase.integral = 100;

%% 04.设置GPOPS求解器参数
%-------------------------------------------------------------------------%
%---------------------------- 设置求解器参数 -----------------------------%        
%-------------------------------------------------------------------------%
setup.name = 'Vehicle-Stopping-OCP';
setup.functions.continuous  = @vsopcContinuous;
setup.functions.endpoint   	= @vsopcEndpoint;
setup.bounds                = bounds;
setup.guess                 = guess;
setup.nlp.solver            = 'snopt';
setup.derivatives.supplier  = 'sparseCD';
setup.derivatives.derivativelevel = 'second';
setup.mesh.method           = 'hp1';
setup.mesh.tolerance        = 1e-6;
setup.mesh.maxiteration     = 45;
setup.mesh.colpointsmax     = 4;
setup.mesh.colpointsmin     = 10;
setup.mesh.phase.fraction   = 0.1*ones(1,10);
setup.mesh.phase.colpoints  = 4*ones(1,10);
setup.method = 'RPMintegration';

%% 05.求解
%-------------------------------------------------------------------------%
%----------------------- 使用 GPOPS2 求解最优控制问题 --------------------%
%-------------------------------------------------------------------------%
output = gpops2(setup);
solution = output.result.solution;
toc;

%% 06.画图
figure('Color',[1,1,1]);
plot(solution.phase.time(:,1),solution.phase.state(:,1),'-','LineWidth',1.5);hold on;
plot(solution.phase.time(:,1),solution.phase.state(:,2),'-.','LineWidth',1.5);
plot(solution.phase.time(:,1),solution.phase.control(:,1),'--','LineWidth',1.5);
axis([0 2 -2.5 2]);
xlabel('Time',...
       'FontWeight','bold');
ylabel('States',...
       'FontWeight','bold');
legend('Pos','Vel','Acc',...
       'LineWidth',1,...
       'EdgeColor',[1,1,1],...
       'Orientation','horizontal',...
       'Position',[0.5,0.93,0.40,0.055]);
set(gca,'FontName','Times New Roman',...
        'FontSize',15,...
        'LineWidth',1.3);
print -dpng Result.png

%% 函数模块部分
% ----------------------------------------------------------------------- %
% ------------------------- BEGIN: vsopcContinuous.m -------------------- %
% ----------------------------------------------------------------------- %
function phaseout = vsopcContinuous(input)
    t  = input.phase.time;
    x2  = input.phase.state(:,2);
    u   = input.phase.control(:,1);

    dx1 = x2;
    dx2 = u;

    phaseout.dynamics = [dx1, dx2];
    phaseout.integrand = 0.5*u.^2;
end
% ----------------------------------------------------------------------- %
% -------------------------- END: vsopcContinuous.m --------------------- %
% ----------------------------------------------------------------------- %

% ----------------------------------------------------------------------- %
% -------------------------- BEGIN: vsopcEndpoint.m --------------------- %
% ----------------------------------------------------------------------- %
function output = vsopcEndpoint(input)
    J  = input.phase.integral;
    output.objective = J;
end
% ----------------------------------------------------------------------- %
% --------------------------- END: vsopcEndpoint.m ---------------------- %
% ----------------------------------------------------------------------- %

欢迎通过邮件联系我：lordofdapanji@foxmail.com

来信请注明你的身份，否则恕不回信。

雷烈