纳什均衡的DQN解法:Nash-DQN
纳什均衡的DQN解法:Nash-DQN
作者
Philippe Casgrain 1, Brian Ning 2 and Sebasitan Jaimungal 2
原文
Available at: https://arxiv.org/abs/1904.10554
摘要
多智能体随机博弈的无模型学习是一个活跃的研究领域。然而,现有的强化学习算法往往局限于零和博弈,而且只适用于较小的状态-行动空间或其他简化设置。在这里,我们开发了一种新的数据高效深度-Q-学习方法,可以无模型地学习一般和随机博弈的纳什均衡。该算法使用了局部线性-二次展开的随机博弈,从而得到可分析求解的最优行动。该展开由深度神经网络参数化,使其具有足够的灵活性来学习环境,而无需体验所有的状态-行动对。我们研究了源于标签不变随机博弈的算法的对称属性,并将我们的算法应用于学习竞争性电子市场中的最优交易策略,作为概念证明。
1. 引言
在自然科学和社会科学中,对相互作用系统的均衡状态的研究无处不在。研究这些均衡的经典方法要求建立一个相互作用系统的模型,求解其均衡,然后研究其属性。然而,这种方法经常会遇到复杂的问题,因为必须在(1)模型的可操作性和(2)模型捕捉其所要代表的数据的主要特征的能力之间取得平衡。这些方法背后的主要思想是从模拟或观察数据中直接逼近平衡点,为常规方法提供了有力的替代方案。
现有关于强化学习(Reinforcement learning,RL)的文献大多集中于单人博弈,局限于零和博弈情况中。
近来有研究将RL扩展到具有虚拟博弈[^hu(2019)]或迭代固定点方法[^lanctot(2017)]的一般和棋博弈中。该类方法要么因其博弈规模巨大或博弈复杂度高导致难以计算均衡点,要么无法对复杂的博弈行为建模。
Hu and Wellman[^hu(2003)]提出了一种基于Q学习的非零和随机博弈NE求解方法。该类方法除了最简单的例子外,在计算上都是不可行的,并且该类方法不适用于局中人选择连续值控制的博弈,也不适用于具有高维博弈状态表示或有大量局中人的博弈。
特别地,我们将状态作用值(Q)函数分解为值函数和优势函数的和。利用神经网络对价值函数进行逼近,并利用神经网络给出的特征系数的非线性函数,局部逼近智能体行为中的优势函数为线性二次函数。这使我们能够根据网络参数分析计算特征空间中每个点的纳什均衡点(即所有智能体的最优行为)。使用这个封闭的局部纳什均衡点,我们推导出一个迭代的参与者-评论者算法来学习网络参数。
该方法的优点:
- 可以处理具有大量博弈状态特征和大动作空间。
- 使用平均场博弈。
- 虽然对Q函数近似结果具有局部结构的限制,但在大多数情况下,所提出的近似算子是充分表达的,在本文给出的数值例子中表现良好。
本文结构如下:
第 2 节介绍了一般和随机博弈的通用马尔科夫模型。第 3 节提出了随机博弈的最优性条件,并激发了我们寻找纳什均衡点的 Q-learning 方法。第 4 节介绍了我们对 Q 函数的局部线性二次逼近以及由此产生的学习算法。我们还提供了标签不变博弈中出现的几种简化方法。第 5 节介绍了实现细节。第 6 节介绍了一些示例。
2. 模型设置
| 我们考虑一个随机博弈,其中有$N$个智能体$i \in \mathfrak{N} := {1,2,\dots,N}$一起竞争。我们假设博弈的状态通过随机过程${x_t}{t \in \mathbb N}$来表示,使得对于每个时间$t$,$x_t \in \mathcal X$,其中$\mathcal{X}$是某个可分的巴拿赫空间。在每个时间$t$,智能体$i$选择一个动作$u{i,i} \in \mathcal U_i$,其中$\mathcal U_i$被假设为一个可分的巴拿赫空间$\mathcal{X}$。在后续中,我们使用符号$\boldsymbol u_{-i,t}=(u_{j,t}){j \in \mathfrak N \textbackslash {i}}$来表示除智能体$i$之外的所有智能体在时间$t$的动作向量,使用符号$\boldsymbol u_t = (u{j,t}){j \in N}$来表示所有智能体的动作向量。我们假设博弈是一个具有完全可见博弈状态的马尔可夫决策过程(MDP)。MDP 假设等同于假设联合状态-动作过程$(x_t,\boldsymbol u_t)^{\infty}{t=1}$是马尔可夫的,其状态转移概率由平稳马尔可夫转移核$p(x_{t+1} | x_t,\boldsymbol u_t)$和初始状态$p_0(x_0)$的分布定义。 |
在的每一个步骤中,智能体都会根据当前的博弈状态、自己的行动选择以及其他智能体的行动来获得不同的奖励。智能体$i$的奖励由函数$(x,u_i,\boldsymbol{u}t) \rightarrow r_i(x;u_i,\boldsymbol{u}{-i}) \in \mathbb{R}$表示,其中$x$表示博弈状态,$u_i$表示智能体的行动,$\boldsymbol{u_{-i}}$表示其他智能体的行动。因此,在每个时间$t$,智能体$i$都会累积奖励$r_i(x_i;u_{i,t},\boldsymbol{u}{-i,t})$。我们假设每个函数在上是连续可微且凹的,在$x$和$\boldsymbol{u}{-i}$上是连续的。
在每个时间$t$,智能体$i$ 可以观察到其他智能体的行动$\boldsymbol{u}{-i,t}$以及博弈状态$x_t$。此外,每个智能体$i$根据确定性马尔可夫策略$\mathcal{X} \ni x \rightarrow \pi _i(x) \in U_i$选择他们的行动。智能体$i$的目标是选择策略$\pi_i$,以最大化目标函数$\mathcal R_i$,该函数表示在给定自身固定策略$\pi_i$ 和其他所有玩家固定策略$\pi{-j}$的情况下,他们在博弈剩余过程中的个人预期折扣未来奖励。智能体$i$的目标函数为
\[\mathcal R_i(x;\pi_i,\boldsymbol \pi_{-i}) = \mathbb{E} [\sum^{\infty}_{t=0} \gamma^{-t} r_i(x_t, \pi_{i,t}, \boldsymbol \pi_{-i,t}) ] \tag{1}\]其中,期望是对过程$(x_t){t \in N}$的期望,其中$x_0 = x$,并且我们假设$\gamma_i \in (0,1)$是表示折扣率的固定常数。在方程$(1)$中,我们使用压缩符号$\pi{i,t}:=\pi_i(x_i)$和$\boldsymbol \pi_{-i,t}:=\boldsymbol \pi_{-i}(x_t)$。智能体的目标函数$(1)$明确依赖于所有智能体的策略选择。然而,每个智能体只能控制自己的策略,并且必须在考虑所有其他玩家行为的情况下选择自己的行动。
因此,智能体$i$寻求一种优化其目标函数的策略,但对其他智能体的行动保持稳健。最终,所有智能体的策略形成一个纳什均衡——一组策略$\boldsymbol \pi^(x)={\boldsymbol \pi^i(x)}{i\in \mathfrak{N}}$,使得单个智能体单方面偏离该均衡将导致该智能体目标函数值的降低。正式地,我们说一组策略$\boldsymbol \pi^*$形成一个纳什均衡,如果
\[\mathcal R_i(x;\pi_i,\pi^*_{-1}) \le \mathcal R_i(x;\pi^*_i,\pi^*_{-i}) \tag{2}\]对于所有可允许的策略$\pi_i$和所有$i \in \mathfrak{N}$。非正式地,我们可以将纳什均衡解释为每个智能体同时最大化其自身目标函数的策略,同时以其他智能体的行动为条件。
3. 最优性条件
我们的最终目标是获得一种无需先验动态知识即可获得非合作博弈均衡的算法。为了做到这一点,我们首先确定比上面给出的非合作博弈均衡的形式定义更容易验证的条件。
我们继续推广著名的纳什均衡贝尔曼方程。在保持$\boldsymbol \pi^_{-1}$不变的情况下,我们可以将动态规划原理应用于智能体$i$奖励$R_i(x;\pi^i,\boldsymbol \pi^*{-i})$,从而导致
\[\mathcal R_i(x;\pi^*_i,\boldsymbol \pi^*_{-i})=\max_\limits{u\in U_i}\left \{r_i(x,u,\boldsymbol \pi^*_{-i}(x))+\gamma_i \mathbb{E}_{x'\sim p(\cdot|x,\boldsymbol u)}[R_i(x';\pi^*_{i,1},\boldsymbol \pi^*_{-i,1})] \right\} \tag{3}\]在非合作博弈均衡下,公式$(3)$同时满足所有$i \in \mathfrak{N}$。
为了更简洁地表达这一点,我们引入了一种向量表示法。首先定义向量函数$\mathcal R(x;\pi)=(\mathcal R_i(s;\pi_i,\pi_{-i})){i \in \mathfrak N}$,由目标函数的堆叠向量组成。我们将在纳什均衡处求值的堆叠目标函数称为堆叠值函数,我们将其写成$V(x):=(V_i(x)){i \in \mathfrak{N}}=\mathcal R(x;\pi^*)$。
接下来,我们定义Nash状态动作值函数,也称为Q-Function,我们表示$\boldsymbol{Q}(x;u):=(Q_i(s;u_i,\boldsymbol u_{-i}))_{i \in \mathfrak{N}}$,其中
\[\boldsymbol{Q}(x;u)=\boldsymbol{r}(x;u)+\gamma_i \mathbb{E}_{x'\sim p(\cdot|x,u)}[\boldsymbol{V}(x')] \tag{4}\]其中我们表示$\boldsymbol{r}(x;u):=(r_i(x,u_i,\boldsymbol{u}{-i})){i \in \mathfrak{N}}$来表示矢量化奖励函数。$\boldsymbol{Q}$的每个元素$Q_i$可以解释为它们的目标函数可能采取的预期最大值,给定固定的当前状态x和所有智能体采取的固定(任意)立即行动$\boldsymbol u$。
接下来,我们定义纳什运算符如下。
定义 3.1 (纳什运算符)考虑$N$个凹实值函数的集合,$\boldsymbol{f}(\boldsymbol u)=(f_i(u_i,\boldsymbol u_{-i})){i \in \mathfrak{N}}$,其中$f_i: U_i \times U{-i} \rightarrow \mathbb{R}$。我们定义纳什运算符$N_{\boldsymbol u \in U} \boldsymbol{f}(\boldsymbol u) \rightarrow \boldsymbol{f}(\boldsymbol u^)$,作为从函数集合到它们的非合作博弈均衡值$\boldsymbol{u}^ \in \mathbb{R}^N$的映射,其中$\boldsymbol{u}^* = \arg N_{\boldsymbol u \in U}\boldsymbol{f}(\boldsymbol u)$为独特点,定义为
\[f_i(\omega_i,\boldsymbol{u}^*_{-i}) \le f_i(u_i,\boldsymbol{u}^*_{-i}),\quad \forall \omega_i \in U_i, \text{and} \ \forall i \in \mathfrak{N} \tag{5}\]对于足够规则的函数$f$集合,Nash运算符对应于在它们的第一个参数$u_i$中同时最大化每个$f_i$。
这个定义为我们提供了值函数和智能体的Q函数之间的关系,即$\boldsymbol{V}(x)=\mathcal N_{\boldsymbol{u} \in U} \boldsymbol{Q}(x;u)$。使用纳什算子,我们可以将Bellman方程$(3)$以简洁的形式表示为
\[\boldsymbol V (x) = N_{\boldsymbol u \in U} \boldsymbol Q(x;u) = N_{\boldsymbol u \in U} \left \{ \boldsymbol{r}(x;u)+\gamma_i \mathbb{E}_{x'\sim p(\cdot|x,u)}[\boldsymbol{V}(x')] \right \} \tag{6}\]在本文的其余部分,我们将其称为纳什-贝尔曼方程。值函数方程$(6)$的定义意味着$\pi^=N_{\boldsymbol u \in U} \boldsymbol Q(s;u)$。因此,为了识别非合作博弈均衡$\pi^$,获得Q函数并将纳什算子应用于它就足够了。这一原则将为我们在 本文的其余部分:不是通过方程$(1)$和$(2)$直接搜索纳什均衡的策略集合空间,我们可以依靠识别满足$(6)$的函数$\boldsymbol Q$,然后计算$\boldsymbol \pi^*=N_{\boldsymbol u \in \mathcal U} \boldsymbol Q (x;\boldsymbol u)$。
4. 局部线性二次纳什Q-learning
在本节中,我们制定了一个算法来学习上一节中描述的随机博弈的非合作博弈均衡。我们采用的方法背后的主要思想是构造一个智能体$i$的$Q$函数的参数估计器$\hat Q^\theta$,我们在其中搜索参数集$\theta \in \Theta$,这导致估计器$\hat Q^\theta$近似满足纳什-贝尔曼方程$(6)$。因此,我们的目标是最小化数量
\[\mathop {\mathop{\mathbb E}\limits_{x \sim \rho}}\limits_{x'\sim p(\cdot|x,\boldsymbol u)} [|| \hat Q^\theta(x;\boldsymbol u) - \boldsymbol r (x;\boldsymbol u) - \gamma_i \mathop{\mathcal{N}}\limits_{\boldsymbol u' \in \mathcal{U}} \hat Q^\theta(x';\boldsymbol u') ||^2 ] \tag{7}\]| 在所有$u$上,我们将$\rho$定义为博弈状态$x$上的无条件概率度量。等式$(7)$被设计为等式$(6)$左右两边之间差距的度量。我们也可以将其解释为$\hat{Q}^\theta$和$\boldsymbol Q$的真值之间的距离。表达式$(7)$是棘手的,因为我们先验地不知道$\rho$也不知道$p(\cdot | x,\boldsymbol u)$,我们希望对系统动力学几乎不做任何假设。因此,我们依赖于基于模拟的方法,近似$(7)$ ,表达式为 |
其中对于每个$m=1,2,\dots,M,(x_m,\boldsymbol u_m;x’_m)$代表从博弈中观察到的过渡三元组。然后我们搜索使$\mathcal{L}(θ)$最小化的$\theta \in \Theta$以近似$\hat Q$。
在我们的算法中,我们做了额外的假设,即博弈状态$x \in \mathcal{X}$和动作用户界面$u_i \in \mathcal{U}i$是实值的。具体来说,我们假设$\mathcal{X} = \mathbb{R}^{d_x}$对于某个正整数$d_x$,$\mathcal{U}_i=\mathbb{R}^{d_i}$对于每个$i \in \mathfrak{N}$,其中$d_1,d_2,\dots,d_N$都是正整数。为了便于记谱,我们定义$d{-i}:=\sum_{j \in \mathfrak{N} \textbackslash {i}} d_{j \cdot}^1$
我们现在为近似$Q$函数的集合定义一个特定的模型$\hat{Q}^{\theta}(x;\boldsymbol u) = (\hat{Q_i^\theta}(x;\boldsymbol u))_{i\ in \mathfrak{N}}$。对于每个$\theta \in \Theta$,我们有$\hat{Q}^\theta: \mathcal{X}\times\mathcal{U} \rightarrow \mathbb{R}^N$并将Q函数分解为两个部分,表达式为
\[\hat{Q}^{\theta}(x;\boldsymbol u)=\hat V^{\theta}(x)+\hat{\boldsymbol{A}}^\theta (x;\boldsymbol{u}) \tag{9}\]其中$\hat{V}^\theta(x)=(\hat{V}^\theta_i(x)){i \in \mathfrak{N}}$是值函数集合的模型,因此$\hat{V}^\theta:\mathcal{X}\rightarrow \mathbb{R}^N$,其中$\hat{\boldsymbol{A}}^\theta(x;\boldsymbol{u})=(\hat{\boldsymbol A}_i^\theta(x;\boldsymbol u)){i \in \mathfrak{N}}$是我们所说的优势函数集合。优势函数代表$\hat{Q}$和$\hat{V}$之间的最优性差距。我们进一步假设对于每个$i \in \mathfrak N$,$\hat{A}^\theta_i$具有线性二次形式 ,表达式为
\[\hat{A}^\theta_i(x;\boldsymbol u)=-\binom{u_i-\mu_i^\theta(x)}{u_i-\mu_i^\theta(x)}^\top \boldsymbol{P}^\theta_i(x)\binom{u_i-\mu_i^\theta(x)}{\boldsymbol u_{-i}-\mu_{-i}^\theta(x)} + (\boldsymbol u_{-i} - \boldsymbol \mu^\theta_{-i}(x))^\top \boldsymbol{\Psi}^\theta_i(x) \tag{10}\]其中,块矩阵为
\[\boldsymbol P^\theta_i(x):=\begin{pmatrix} P^\theta_{11,i}(x) & P^\theta_{12,i}(x) \\ P^\theta_{21,i}(x) & P^\theta_{22,i}(x) \end{pmatrix} \tag{11}\]对于每一个$i \in \mathfrak N$而言,$\mu_i^\theta(x):\mathcal{X}\rightarrow\mathbb{R}^{d_i}$,且 $\boldsymbol{\mu}{-i}^\theta(x)=(\mu_i^\theta(x)){i \in \mathfrak{N}}$。$\boldsymbol{\Psi}i:\mathcal{X}\rightarrow\mathbb{R}^{d{-i}}$ 。在式$(11)$中,$P_{11,i}^\theta:\mathcal{X}\rightarrow\mathbb{R}^{d_i\times d_i}$,$P_{12,i}^\theta:\mathcal{X}\rightarrow\mathbb{R}^{d_i\times d_{-i}}$,$P_{21,i}^\theta:\mathcal{X}\rightarrow\mathbb{R}^{d_{-i}\times d_i}$,$P_{22,i}^\theta:\mathcal{X}\rightarrow\mathbb{R}^{d_{-i}\times d_{-i}}$为矩阵值函数。要求$P_{11,i}^\theta(x)$对于所有$x \in \mathcal{X}$而言都是正定的。并且不失一般性,可以选择$P_{12,i}(x)=(P_{21,i}(x))^\top$,因为优势函数只取决于$P_{12,i}$和$P_{21,i\cdot}$。
因此,我们没有建模$\hat{Q}^\theta(x;\boldsymbol u)$,而是将函数$\hat V^\theta,\boldsymbol \mu^\theta$和${\boldsymbol P_i^\theta,\boldsymbol \Psi_i^\theta}{i \in \mathfrak N}$分别建模为状态空间X的函数。这些函数中的每一个都可以用通用函数逼近器(如神经网络)建模。唯一的主要限制是$P{11,i}^\theta(x)$必须保持$x$的正定函数。这种限制很容易通过使用乔莱斯基分解分解$P_{11,i}^\theta(x)$来实现,因此我们编写$P_{11,i}^\theta(x)=(L_{11,i}^\theta(x))^\top$,而是对下三角形矩阵$L_{11,i}^\theta \in \mathbb{R}^{d_i \times d_i}$建模。
$(10)$中的模型假设隐含地假设智能体$i$的Q函数可以近似写成每个智能体动作的线性二次函数。人们可以通过考虑非合作博弈均衡周围变量$u$中$Q_i$的二阶泰勒展开,以及$Q_i$是其输入用户界面的凸函数的假设来等价地激发这种近似。然而,这种扩展不假设$Q_i$对博弈状态$x$值的依赖。
设计了$(10)$的形式,使得每个$\hat{Q}i^\theta(x;u_i,\boldsymbol{u}{-i})$都是用户界面的凹函数,保证了$\mathcal{N}_{u \in \mathcal{U}} \hat{Q}$是双射的。此外,在我们的模型假设下,在点$u^*(x)=\boldsymbol{\mu}(x)$处达到纳什均衡,此时优势函数为零,因此我们得到了值函数和均衡策略的简单表达式
\[\hat{V}^\theta(x)=\mathop{\mathcal{N}}_{u\in\mathcal{U}}\hat{Q}^\theta(x;\boldsymbol u) \quad \text{and} \quad \boldsymbol{\mu}(x)=\arg \mathop{\mathcal{N}}_{u \in \mathcal{U}} \hat{Q}^\theta(x;\boldsymbol{u}) \tag{12}\]因此,我们的模型允许我们通过函数$\boldsymbol \mu^\theta$和$\hat{V}^\theta$直接指定非合作博弈均衡策略和每个智能体的值函数。这种简化的结果是方程$(8)$中损失函数的求和,其中包含纳什均衡本身以前是难以处理的,但现在变得可以处理了。对于每个样本观察 $m$(由状态$x_m$、$u_m$和新状态$x’_m$组成),我们然后有一个损失
\[\mathcal{L}(\theta) = ||\hat{V}^\theta(x_m)+\hat{\boldsymbol A}^\theta(x_m;\boldsymbol u_m)-\boldsymbol r(x_m;\boldsymbol u_m)-\gamma_i \hat{V}^\theta(x'_m)||^2 \tag{13a}\]而剩下的就是尽量减少总损失,即
\[\mathcal{L}(\theta) = \frac{1}{M}\sum_{m=1}^M \mathcal{L}_m(\theta) \tag{13b}\]在给定参数$\theta$观察状态-动作三元组$(x_m,\boldsymbol u_m,x’m)^M{m=1}$。
4.1. 简化博弈结构
等式$(10)$需要函数$\hat{V}^\theta,\boldsymbol \mu^\theta,{\boldsymbol P^\theta_i,\boldsymbol \Psi_i}_{i \in \mathfrak{N}}$的参数模型,这可能导致非常大的参数空间,原则上需要许多训练步骤。然而,在许多情况下,博弈的结构可以显着降低参数空间的维度,并导致易于学习的模型结构。以下小节列举了这些典型的简化。
标签不变性
许多博弈都有对称的玩家,因此对玩家标签的排列是不变的。这种标签不变性意味着每个智能体-i不会区分其他博弈参与者,智能体的奖励功能独立于所有其他智能体状态和/或行为的任何重新排序。
更正式地说,我们假设对于任意智能体$i$,博弈的状态可以表示为$x=(x_0,x_i,x_{-i})$,其中$x_0$表示不属于任何智能体的博弈状态部分,$x_i$表示属于智能体$i$的博弈状态部分,$x_{−i}={x_j}{j\in\mathfrak{N}/{i}}$表示属于其他智能体的博弈状态部分。接下来,让我们表示$N-1$引集上的排列集,其中对于每个$\lambda \in \Lambda$,我们将集合的排列表示为$\lambda({y_j}{j=1}^{N-1})={y_{k(j)}}_{j=1}^{N-1}$,其中$k:{1,\dots,N-1}\rightarrow{1,\dots,N-1}$是一对一的,并且从集合的索引映射到自身。
标签不变性等价于假设对于任何$\lambda \in \Lambda$,每个智能体的奖励函数满足
\[r_i(x_0,x_i,\lambda(x_{-i});u_i,\lambda(u_{-i}))=r_i(x_0,x_i,x_{-i};u_i,u_{-i}) \tag{14}\]有了这样的标签不变性,$(10)$中优势函数的线性二次展开的形式就简化了。假设$d_j=d$,对于所有$j \in \mathfrak{N}$,仅智能体动作中的独立厂牌不变性要求$\hat{A}_i$具有简化形式
\[\begin{aligned} \hat{A}_i^\theta(x;\boldsymbol u)=&-||u_i-\mu_i^\theta(x)||^2_{p_{11,i}^\theta(x)}-\sum_{j \in \mathfrak{N}/\{i\}}\langle (u_i-\mu_i(x)^\theta),(u_j-\mu_j^\theta(x))\rangle_{p_{12,i}^\theta}(x)\\ &-\sum_{j \in \mathfrak{N}/\{i\}}||u_j-\mu_j^\theta(x)||_{p_{22,i}^\theta(x)}+\sum_{j \in \mathfrak{N}/\{i\}} (u_j-\mu_j^\theta(x))^\top \boldsymbol{\psi}^\theta(x) \end{aligned} \tag{15}\]| 对于所有的$i \in \mathfrak{N}$,我们使用记数法$ | z | ^2_M=z^\top Mz$和$\langle y,z \rangle_M=y^\top M z$表示适当大小的矩阵$M$。$(15)$的函数形式允许我们大大减小由$N^2$阶建模的矩阵的大小。 |
为了对状态施加标签不变性,我们要求输入上的置换不变性,函数近似$\hat{V}^\theta,\boldsymbol{\mu}^\theta,{\boldsymbol P_i,\boldsymbol \psi^\theta }{i \in \mathfrak{N}}$。Zaheer等人(2017)提供了神经网络结构置换不变性的充要条件。这种充要结构定义如下。设$\phi: \mathbb{R}^{n_1} \to \mathbb{R}^{n_2}$和$\sigma: \mathbb{R}^{n_2} \to \mathbb{R}^{n_3}$是两个任意函数。从这些函数中,设$f{\text{inv}}:\mathbb{R}^{J \times n_1} \to \mathbb{R}^{n_3}$是这些函数的组成,使得
\[f_{\text{inv}}(z)=\sigma (\sum_{j=1}^J \phi(z_j)) \tag{16}\]很明显,以这种方式构造的$f_{\rm inv}$对$z$分量的重新排序是不变的。等式$(16)$可以解释为通过$\phi$聚合输入的所有维度(这将对应于所有智能体的状态)的层,以及通过$\sigma$将聚合结果转换为输出的层。我们进一步假设$\phi$和$\sigma$都是具有适当输入和输出维度的神经网络。这种结构也可以稍后作为输入嵌入到更复杂的神经网络中。
相同的偏好
很常见的是,所有智能体的允许动作都是相同的,即$\mathcal U_i=\mathcal U$,$\forall v_i \in \mathfrak{N}$,并且智能体具有同质的目标,或者大的智能体子群体具有同质的目标。到目前为止,我们允许智能体分配不同的性能指标,并且通过奖励和折扣率集${r_i,\gamma_i}_{i\in\mathfrak{N}}$来显示变化。如果智能体具有相同的偏好,那么我们只需要假设$r_i(x;\boldsymbol{u})=r(x;\boldsymbol{u})$和$\gamma_i = \gamma$对于所有$i \in \mathfrak{N}$。根据总折扣奖励、状态-动作价值函数和价值函数的定义,相同的偏好和允许动作意味着$\mathcal R_i$、$Q_i$和$V_i$独立于$i$。
此外,相同偏好的假设与标签不变性的假设相结合,可以进一步减少优势函数的参数化。在这个额外的假设下,我们有$\hat V_i$,$\hat A_i$必须对所有$i$都是相同的,这将所有$\hat V^\theta_i$,$\mu_i^\theta$,$\boldsymbol P_i^\theta$,$\boldsymbol \psi^\theta$的建模简化为对单个$i$的建模。这进一步减少了必须以$N$为序建模的函数的数量。标签不变性和相同偏好的综合效应具有复合效应,这可能对建模任务产生很大影响,特别是在考虑大量玩家时。
备注4.1(子种群不变性和偏好):我们也可以考虑标签和偏好不变性发生在智能体子种群内而不是整个种群内的情况。例如,在某些智能体可能与其他智能体合作的博弈中,我们可以假设智能体对合作者和非合作者分别重新标记无动于衷。同样,我们可以考虑智能体组共享相同性能指标的情况。除其他外,这种情况会导致类似于等式(15)的建模简化,并且可以开发简化的神经网络结构。出于空间的考虑,我们不开发进一步的简化示例。 例如,我们也不声称我们提供的列表是详尽无遗的,因为人们可以很容易地想象出许多其他可能感兴趣的几乎对称的情况。
5. Nash Actor-Critic算法的实现
利用优势函数的局部线性二次形式,以及上一节中概述的简化假设,我们现在可以通过迭代优化和采样方案最小化目标$(8)$,目标$(8)$减少到参数θ上的总和$(13a)$。原则上,人们可以应用一个简单的随机梯度下降方法,在适当的损失函数上使用反向传播。相反,我们提出了一种Actor-Critic风格的算法来提高算法的稳定性和效率。Actor-Critic方法(例如,见Konda和Tsitsiklis 2000)已经被证明可以提供强化学习方法对其最优解更快、更稳定的收敛,我们的模型自然地适合这种方法。
等式$(9)$中的分解允许我们独立于其他分量对值函数$\hat V$进行建模。因此,我们采用Actor-Critic更新规则,通过分离参数集$\theta=(\theta_V,\theta_A)$来最小化损失函数$(13a)$,其中$\theta_V$表示建模的参数集$\hat V^{\theta_V}$,$\theta_A$表示建模的参数集$\hat{ \boldsymbol{A}}^{\theta_A}$。我们提出的Actor-Critic算法通过最小化总损失来更新这些参数 ,总损失可表示为
\[\frac{1}{M} \sum_{m=1}^M \hat L (y_m,\theta_V,\theta_A) \tag{17a}\]其中与纳什-贝尔曼方程中的误差相对应的单个样本损失,在已经求解纳什均衡之后,是
\[\hat L (y_m,\theta_V,\theta_A) = ||\hat V^{\theta_V}(x_m) + \hat{\boldsymbol{A}}^{\theta_A}(x_m;\boldsymbol{u}_m)-\boldsymbol r (x_m;\boldsymbol{u}_m)-\gamma_i \hat V ^{\theta_V}(x'_m)||^2 \tag{17b}\]对于$\boldsymbol{u}_m$,$y_m=(x_m,\boldsymbol u_m,x’_m)$,我们通过在变量$\theta_A$和$\theta_V$的最小化之间交替来最小化损失。
算法1为我们的最佳化问题提供了Actor-Critic程序的大纲。我们包括一个重放缓冲区并采用迷你批处理。重放缓冲区是以前经历过的过渡元组的集合,形式为$y_t=(x_{t−1},\boldsymbol u,x_t)$,表示系统的先前状态、在该状态下采取的行动、系统的结果状态以及过渡期间的奖励。我们从重放缓冲区中随机采样一个迷你批处理,以使用SGD更新模型参数。该算法还使用了朴素的高斯探索策略,尽管它可能会被任何其他动作空间探索方法所取代。在$\theta_V$和$\theta_A$上的优化步骤期间,我们使用随机梯度下降或任何其他自适应优化方法。
算法步骤如下。

6. 实验
我们在电子交易所统计套利的多智能体博弈上测试我们的算法,该博弈由受其行为影响的具有随机价格过程的单一资产交易的智能体组成,该模型的一个更简单的版本已经在卡斯格伦和杰蒙加尔(2018,2020)以及纽曼和沃(2021)中进行了研究。在这些作品中,在各种假设下,作者采用平均场方法,并证明平均场最优策略为有限玩家情况提供了近似的非合作博弈均衡。
在我们的设置中,任意智能体$i$,$i\in \mathfrak{N}$,可以在交易期限期间$t \in \mathfrak{T}:=[0,T]$以$v_{i,t} \in \mathbb{R}$的比率购买或出售资产。在$t=T$时,智能体必须清算其持有的资产,任何剩余的库存都将受到最终处罚。智能体可以在时间$t_1,t_2,\dots,t_M$(决策点)的离散特定点改变其交易率。假设任何两个决策点之间的交易率是恒定的,因此在这段时间$(t_m,t_{m+1})$内交易的资产总量由$v_{i,t_m}^T=(t_{m+1-t_m})v_{i,t_0}$给出。每个智能体-i跟踪他们的库存$q_{i,t_m}=q_{i,0}+\int_0^{t_m} v_{i,t} \text{d}t$。库存对其他智能体是不可见的,但总订单流,即$\sum_{i \in \mathfrak{N}}(q_{i,t}-q_{i,0})$是。为了便于表示,我们假设$t \in {t_1,t_2,\dots,t_M}$。我们假设资产价格过程$S_t$根据以下连续时间动态系统演变:
\[\text{d}S_t=(\mu(S_t)+g(\boldsymbol{v_t}))\text{d}t+\text{d}Y_t+\sigma\text{d}W_t \tag{18}\] \[\text{d}Y_t = - \rho Y_t \text{d}t+\gamma h(v_t)\text{d}t \tag{19}\]初始条件$S_0$,方差$\sigma>0$,布朗运动$(W_t)t≥0$。此外,我们用 $\boldsymbol ν = ((ν{i,t}){i\in\mathfrak{N}}){t\ge0}$表示交易率的向量值过程,并用$\bar{v}t=\sum{i \in \mathfrak{N}} v_{i-t}$表示时间$t$的总交易率。上述形式假设所有智能体的累积交易通过$Y:=(Y_t)_{t\ge0}$引起短暂影响和通过$g$引起永久影响。
函数$\mu$和$g$分别表示均值过程和永久价格影响,对于这里进行的实验,我们假设过程均值-回复使得$\mu(S)=\kappa (\theta-S)$,其中$\kappa>0$表示均值-回复率,$\theta$表示均值回复水平,此外,我们假设线性永久价格影响,使得$g(\boldsymbol v)=\eta \bar v$. 累积瞬态价格影响假设为平方根,即$h(\boldsymbol v)= \text(sign)(\bar v) \sqrt{\bar v}$ 在这些模型假设下,可以写出连续动力学
\[\text{d}S_t=(\kappa(\theta - S_t)+\eta \bar v _t)\text{d}t+\text{d}Y_t+\sigma W_t \tag{20}\] \[\text{d}Y_t = - \rho Y_t \text{d}t + \gamma\ \text{sign}(\bar v_t)\sqrt{\bar v_t} \text{d}t \tag{21}\]此外,每个智能体支付的交易成本与他们在每个时间段内买卖的金额成正比。这代表了智能体从“走限价订单簿”中产生的成本,通常取决于资产的流动性。智能体跟踪他们交易的总现金,我们用$X_i:=(X_{i,t}){t\ge 0}$表示相应的过程,其中$X{i,t}=-\int_0^T v_{i,t} (S_t+b_1 v_{i,t}) \text{d}t$,并且$b_1>0$是交易成本常数。
智能体人的目标是最大化(i)他们在时间$T$拥有的总现金,(ii)时间$T$的超额风险敞口和(iii)风险承担的惩罚。我们将智能体人的目标(总预期回报)表述为
\[\mathcal{R}_i := \mathbb{E}[X_{i,T}+q_{i,T}(S_T-b_2 q_{i,T})-b_3 \int_0^T q_{i,t}^2 \text{d}t] \tag{22}\]其中$b_2,b_3>0$。在等式$(22)$中,第二项是在时间$T$瞬间清算库存的成本,最后一项是承担与每个时间段持有量的平方成比例的超额风险的惩罚——所谓的紧迫性惩罚。在这个目标函数中,所有智能体人交易行为的影响通过$S$的动力学隐含地出现,并通过它对现金过程$X_i$的影响。这种特殊形式的目标假设智能体人具有相同的偏好,这些偏好对智能体重新标记是不变的。因此,我们可以采用第4.1节中讨论的技术来简化优势函数$\hat A$的形式。在我们的示例中,我们使用包含置换不变层的神经网络对优势函数$\hat A$的每个组件进行建模。
我们的实验假设在$5$小时$(T=5)$和10个相同持续时间的决策点$(M=10)$的时间范围内总共有$5$个智能体。
6.1 特点
我们使用以下特征来表示环境在时间$t$的状态$x_t$:
- Price($S_t$):表示资产当前价格的标量,
- Time($t$):表示智能体在时间范围内所处的当前时间步长的标量,
- 总订单流($\boldsymbol{\sum_{i\in\mathfrak{N}}q_{i,0}-q_{i,t}}$):表示自交易期开始以来来自所有智能体的总订单流的标量,以及
- 累积瞬态价格影响($Y_t$):表示影响价格的当前瞬态价格影响水平的标量。
假设所有特征都是非标签不变的。
6.2 网络细节
优势函数逼近$\hat{\boldsymbol A}^{\theta_A}$的网络结构由两个网络组件组成:(i)馈入(ii)主网络层的置换不变层。 置换不变层的输入是标签不变特征。如第4.1节所述,该层是一个全连接的神经网络,具有三个隐藏层,每个隐藏层包含20个节点。层通过SiLU激活函数(Elfwing、Uchibe和Doya 2018)连接。然后,我们稍后将此置换不变的输出与非标签不变特征相结合,它们一起构成主网络的输入。主网络由四个隐藏层组成,每个隐藏层有32个节点。该主网络的输出是第4节中定义的近似优势函数的参数$\boldsymbol \mu$和${\boldsymbol P_i^\theta,\boldsymbol \Psi_i}_{in \in \mathfrak{N}}$。这些参数完全指定了优势函数的值。

值函数近似$\hat{\boldsymbol A}^{\theta_A}$的网络结构包含四个隐藏层,每个隐藏层有32个节点。该网络采用第6.1节中描述的所有状态的特征,并输出所有智能体的近似值函数。
我们使用具有小批量和0.001权重衰减的Adam优化器(Loshchiov和Hutter 2018)来优化第5节中定义的损失函数。小批量大小设置为在$[0,T]$期间执行的十个完整集。学习率设置为0.003,并在整个训练过程中保持不变,仅由优化器的权重衰减修改。训练最多执行20,000次迭代,提前停止标准是最近3000次迭代中的损失没有改善。
6.3 基线虚拟博弈
由Brown(1951)首次提出的虚构博弈(Fictitify Play,FP)是确定多主体博弈纳什均衡的经典方法。它已被证明在零和博弈(Brown 1951)、潜在博弈(Monder和Shapley 1996)、具有一般收益的2×N博弈(Berger 2005)的两个玩家情况下收敛,并且经常被用作许多现代方法的基础(Heinrich、Lanctot和Silver 2015)。一般来说,FP假设每个玩家遵循一个固定的混合策略,该策略在每次迭代中通过对对手先前策略的经验平均值做出最佳响应来更新。在我们的实验中,我们假设相同的智能体,因此在每次迭代中计算单个智能体的最佳响应就足够了。具体来说,让$\boldsymbol{u}i^F(x){i \in \mathfrak{N}}$是每个智能体的最佳FP策略,我们使用算法2中定义的算法来获得。
为了获得算法2第2行中智能体$i$对其他智能体策略的最佳响应,我们使用深度确定性策略梯度(DDPG)(Lillicrapet al.2015)。DDPG使用神经网络来表示最佳策略和状态-动作值函数。与我们的Nash-DQN方法一样,这种方法不知道智能体的奖励函数或转换动态,因此为我们的Nash-DQN提供了一个公平的比较。然而,由于DDPG与FP结合的性质,它是高度数据和训练效率低下的,因为每个FP迭代都需要优化DDPG策略 DDPG的每次迭代使用的资源量与我们的Nash-DQN方法的完整训练周期大致相同。
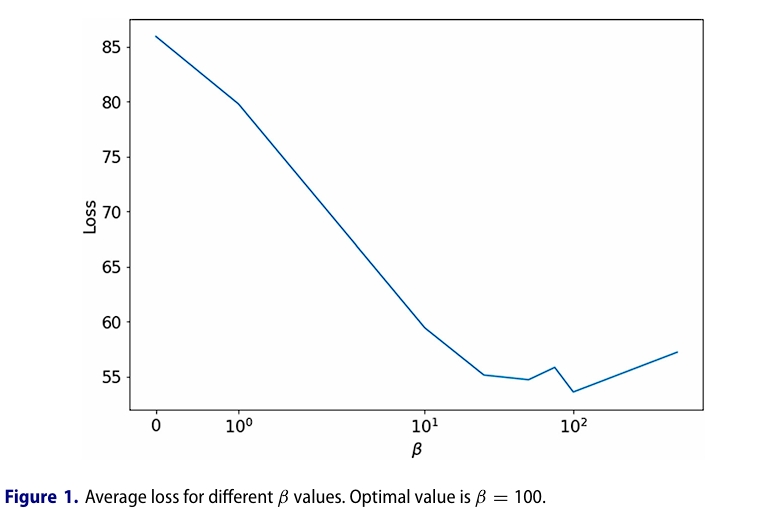

6.4 优化改进
我们发现,直接最小化方程$(17a)$有时会在最终策略中产生不准确,这是由于优势函数方程$(15)$中使用的学习参数的大小不同,特别是线性项中添加L1正则化项
\[\hat{L}(y_m,\theta_V,\theta_A):=\hat{\mathcal{L}}(y_m,\theta_V,\theta_A)+\beta ||\boldsymbol{\psi}^\theta(x)|| \tag{23}\]显着提高了性能。
超参数$\beta$的最优值是通过最小化在1000个随机生成的模拟中计算的平均损失方程$(17a)$来确定的。图1表明β=100的值是最优的。
6.5 仿真结果
我们在分析中使用表1中所示的一组模型参数。
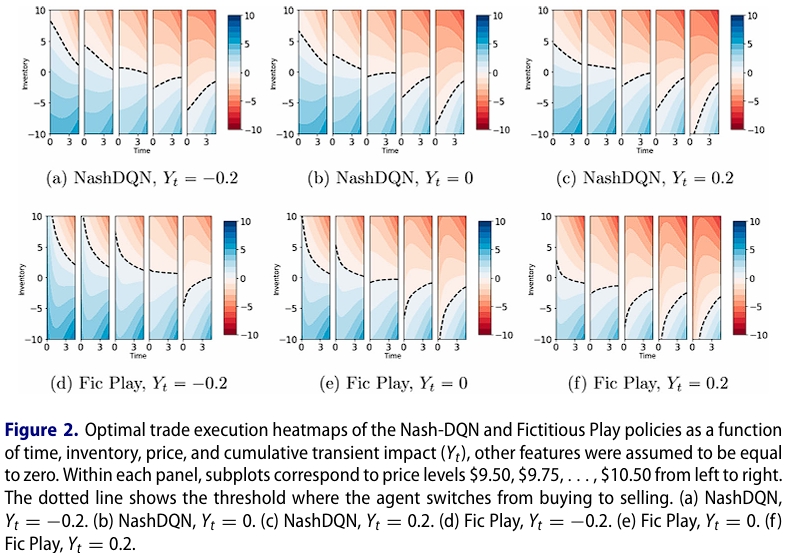
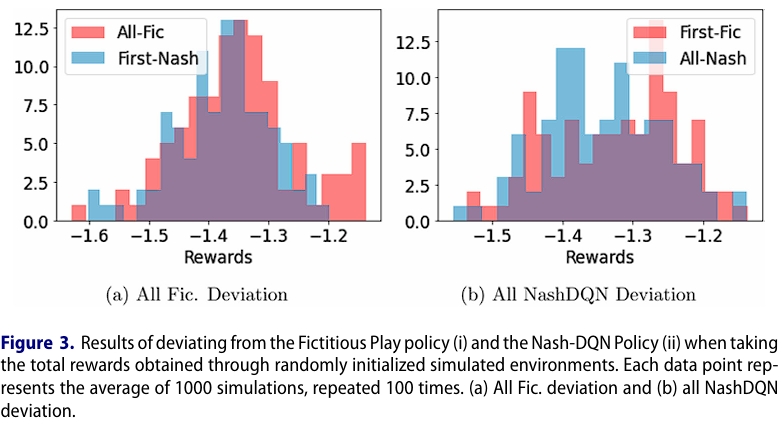
图2显示了通过我们的Nash-DQN方法和FP方法获得的最佳策略。我们可以看到,尽管数据效率显着提高,但最佳策略本质上是相同的。为了评估Nash-DQN方法的性能,我们 考虑以下两个场景:(i)智能体1跟随Nash-DQN和所有其他智能体FP与所有智能体跟随FP,(ii)智能体1跟随FP和所有其他智能体Nash-DQN与所有智能体跟随Nash-DQN。接下来,我们使用模拟环境将这些策略应用于1000条路径。最后,我们平均总奖励,重复整个练习100次,并绘制出结果分布,如图3所示。从图中可以看出,分布中没有明显的差异。事实上,FP和Nash-DQN的结果均值不同的零假设不能在5%的水平上被拒绝。
7. 结论
在这里,我们提出了一个用于多智能体(随机)博弈的计算上可处理的强化学习框架。我们的方法在将智能体的状态-动作值函数集合分解为单个值函数及其优势函数之后利用函数逼近。此外,我们以局部线性二次形式逼近优势函数,并使用神经网络架构来逼近值函数和优势函数。博弈中的典型对称性允许我们使用置换不变神经网络,受Arnold-Kolmogorov表示定理的驱动,来降低参数空间的维数。最后,我们开发了一个演员-批评范式来估计参数,并将我们的方法应用于电子交易中的一个重要应用。我们的方法比传统的FP策略更具数据效率,适用于大量玩家和连续的状态-动作空间。用于训练和生成数字的可执行代码可在https://github.com/p-casgrain/Nash-DQN获得。
还有许多开放的探索之门,包括扩展我们的方法来解释驱动环境的潜在因素,以及当所有主体的状态部分(或完全)对任何个体主体隐藏时。此外,我们的方法可以很容易地应用于平均场博弈,这对应于随机博弈的无限人口极限,其中任何个体主体对状态动态的贡献都是微不足道的。
[^lanctot(2017)]: Lanctot, M, V. Zambaldi, A. Gruslys, A. Lazaridou, K. Tuyls, J. Pérolat, D. Silver, and T. Graepel2017. “A Unified Game-theoretic Approach to Multiagent Reinforcement Learning.” In Advances in Neural Information Processing Systems, 4190-4203. Advances in Neural Information Processing Systems.
[^hu(2003)]: Hu, J., and M. P. Wellman. 2003. “Nash Q-learning for General-sum Stochastic Games.” Journal of Machine Learning Research 4:1039-1069.