一个信号博弈模型的解法

2022-11-14

题目在这里：【北大光华金融硕士考研·微观】不完全信息动态博弈及其代表性经典真题（上）

因为研究中要用到不完全信息动态博弈，所以研究了一下它，在B站上面找到了一个考研题针对不完全信息动态博弈的信号博弈模型进行求解，看完之后我记录下了自己的解题思考，防止自己忘记。

【例】厂商进入的信号博弈

现市场上有一新厂商打算进入市场，而自然决定这个进入者（后称 $p_1$）强弱（$\theta_s$, $\theta_w$），同时在位厂商（后称 $p_2$）不知进入厂商的类型是强（$\theta_s$）还是弱（$\theta_w$），但是可以观察到进入厂商释放的信号是强（S）还是弱（W）。在位厂商可以根据信号决定打（F，fight），还是适应（A，accommodate）

【解】

把收益图画出来。

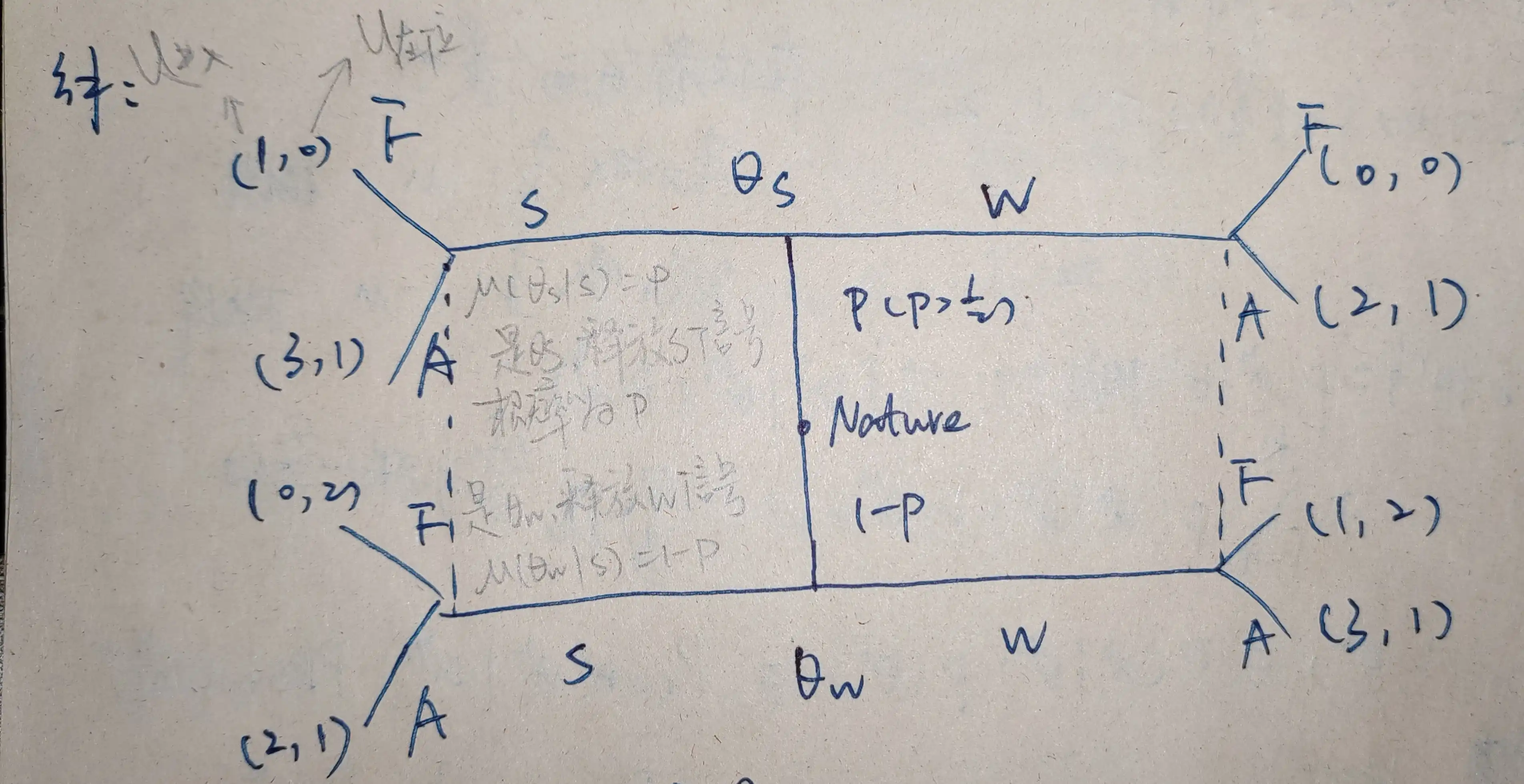
benefit game tree

思考：进入厂商 $p_1$ 有哪些策略：$SS$、$WW$、$SW$、$WS$。

说明：以 $SS$ 为例，第一个 $S$ 的意思是，当 $p_1$ 为 $\theta_s$ 时，发出 $S$ 信号；第二个 $S$ 的意思是，当 $p_1$ 为 $\theta_w$ 时，发出 $S$ 信号。

在位厂商 $p_2$ 有哪些策略：$FF$、$AA$、$FA$、$AF$。

说明：以 $FF$ 为例，第一个 $F$ 的意思是，当 $p_2$ 接受到 $S$ 信号时，作出 $F$ 动作；第二个 $F$ 的意思是，当 $p_2$ 接受到 $W$ 信号时，作出 $F$ 动作。

求解：

(1) 考虑 $S_1=SW$。

解释：$p_1$ 为 $\theta_s$ 时释放 $S$ 信号，$p_1$ 为 $\theta_w$ 时释放 $W$ 信号。

这是“说实话”的情况，那么在贝叶斯信念中，

\[\left\{\begin{matrix} \begin{aligned} \mu(\theta_s|S) &= 1, \\ \mu(\theta_w|W) &= 1. \end{aligned} \end{matrix} \right.\]

那么从博弈树可知，$p_2$ 的策略为：$S_2=AF$

解释：

1) $p_1$ 类型为 $\theta_s$，释放 $S$ 信号， $p_2$ 选择 $A$ 的收益高； 2) $p_1$ 类型为 $\theta_w$，释放 $W$ 信号， $p_2$ 选择 $F$ 的收益高。

分析：由序贯理性可知，若 $p_1$ 知道 $S_2=AF$，则 $p_1$ 在自己类型为 $\theta_w$ 时，释放 $S$ 信号。而 $S_2=AF$，则 $p_2$ 选择 $A$ 策略，此时收益 $B^S=2$ 反而高于 $p_2$ 选 $F$ 的收益 $B^W=1$。那么这样就不是一个精炼贝叶斯均衡（Perfect Bayesian Equilibrium, PBE）

(2) 考虑 $S_1=WS$。

解释：$p_1$ 为 $\theta_s$ 时释放 $W$ 信号，$p_1$ 为 $\theta_d$ 时释放 $S$ 信号。

这是“说谎话”的情况，那么在贝叶斯信念中，

\[\left\{\begin{matrix} \begin{aligned} \mu(\theta_s|S) &= 0, \\ \mu(\theta_s|W) &= 1. \end{aligned} \end{matrix} \right.\]

那么从博弈树可知，$p_2$ 的策略为：$S_2=FA$

解释：

1) $p_1$ 类型为 $\theta_s$，释放 $W$ 信号， $p_2$ 选择 $A$ 的收益高； 2) $p_1$ 类型为 $\theta_w$，释放 $S$ 信号， $p_2$ 选择 $F$ 的收益高。

分析：由序贯理性可知，若 $p_1$ 知道 $S_2=FA$，则 $p_1$ 在自己类型为 $\theta_w$ 时，释放 $W$ 信号。而 $S_2=FA$，则 $p_2$ 选择 $A$ 策略，此时收益 $B^W=3$ 反而高于 $p_2$ 选 $F$ 的收益 $B^S=0$。那么这样就 PBE。

(3) 考虑 $S_1=SS$。

解释：$p_1$ 为 $\theta_s$ 时释放 $S$ 信号，$p_1$ 为 $\theta_d$ 时释放 $S$ 信号。

在贝叶斯信念中，

\[\left\{\begin{matrix} \begin{aligned} \mu(\theta_s|S) &= P, \\ \mu(\theta_s|W) &= 任意值. \end{aligned} \end{matrix} \right.\]

只看左边的树。有：$S_2=AA$

$p_2$ 中，选 $A$ 的收益为 $B^{A}=1$，选 $F$ 的收益为 $B^{F}=0\times P+2\times(1-P)=2(1-P)$，

如果要让 $B^{A} < B^{F}$，则 $2(1-P)<1$，得到

\[P > 1/2.\]

那么结论是，若 $P > 1/2$，

则 $p_2$ 的策略为 $S_2=AA$。

i）然而，也要考虑 $p_1$ 释放 $W$ 的情况（虽然不会出现，也要讨论）

可以发现，$p_2$ 选 $A$ 的收益为 $B^{A}=1$，选 $F$ 的收益为 $B^{F}=0\times \mu(\theta_s|w)+2\times(1-\mu(\theta_s|w))=2(1-\mu(\theta_s|w))$。

因为 $\mu(\theta_s|w) > 1/2$，则 $p_2$ 选择 $F$ 的收益为 $B^{F}=2(1-\mu(\theta_s|w))<1$。

综上，$S_2=AA$。

但是！$p_1$ 为 $\theta_w$ 时可以认为，反正 $p_1$ 出什么信号，$p_2$ 都会选择 $A$ 行为。从博弈树上可以看到，$p_1$ 释放 $W$ 时，收益为 $B^W=3$，$p_1$ 释放 $S$ 时，收益为 $B^S=2$。

那么，$S_1$ 有可能偏离到 $S_1=SW$ 去，所以 $(SS,AA,P)$ 不是PBE。

ii）同样考虑 $p_1$ 释放 $W$ 的情况。有：$S_2=AF$

此时，选 $F$ 的收益为 $B^{F}=0\times P+2\times(1-\mu(\theta_s|w))=2(1-\mu(\theta_s|w))$，

根据 $2(1-\mu(\theta_s|w))>1$，得到 $\mu(\theta_s|w) < 1/2$ 时，$B^{F}>1$。

那么，如果 $p_1$ 为 $\theta_s$ 释放 $W$ 信号，有 $B^{S}=3 \rightarrow B^{W}=0$，是一个下降趋势；

如果 $p_1$ 为 $\theta_w$ 释放 $W$ 信号，有 $B^{S}=2 \rightarrow B^{W}=1$，也是一个下降趋势。

所以， $p_1$ 不能为 $\theta_s$ 时释放 $W$ 信号，也不能为 $\theta_w$ 时释放 $W$ 信号。

综上，$(SS,AF,\mu)$ 为 PBE，但需满足 $\mu(\theta_s|w)\le 1/2,\mu(\theta_s|s)=P$。

(4) 考虑 $S_1=WW$。

解释：$p_1$ 为 $\theta_s$ 时释放 $W$ 信号，$p_1$ 为 $\theta_d$ 时释放 $W$ 信号。

在贝叶斯信念中，

\[\left\{\begin{matrix} \begin{aligned} \mu(\theta_s|w) &= P, \\ \mu(\theta_s|s) &= 任意值. \end{aligned} \end{matrix} \right.\]

只看右边的树。有：$S_2=AA$

$p_2$ 中，选 $A$ 的收益为 $B^{A}=1$，选 $F$ 的收益为 $B^{F}=0\times P+2\times(1-P)=2(1-P)$，

如果要让 $B^{F} < B^{F}$，则 $2(1-P)<1$，得到

\[P > 1/2.\]

那么结论是，若 $P > 1/2$，

则 $p_2$ 的策略为 $S_2=AA$。

i）然而，也要考虑 $p_1$ 释放 $S$ 的情况（虽然不会出现，也要讨论）

可以发现，$p_2$ 选 $A$ 的收益为 $B^{A}=1$，选 $F$ 的收益为 $B^{F}=0\times \mu(\theta_s|s)+2\times(1-\mu(\theta_s|s))=2(1-\mu(\theta_s|s))$。

因为 $\mu(\theta_s|s) > 1/2$，则 $p_2$ 选择 $F$ 的收益为 $B^{F}=2(1-\mu(\theta_s|s))<1$。

综上，$S_2=AA$。

但是！$p_1$ 为 $\theta_s$ 时可以认为，反正 $p_1$ 出什么信号，$p_2$ 都会选择 $A$ 行为。从博弈树上可以看到，$p_1$ 释放 $W$ 时，收益为 $B^W=2$，$p_1$ 释放 $S$ 时，收益为 $B^S=3$。