信息滤波、UD滤波、遗忘滤波和自适应滤波
题目
这次给了四个题目,分别实现了信息滤波、UD滤波、遗忘滤波和自适应滤波,题目还是作业的题目,但是量测频率和时间更新频率都成 $1HZ$ 了。
这里重新给出题目:
巡航导弹沿直线飞向目标,目标处设有一监视雷达,雷达对导弹的距离进行观测。假设(1)导弹初始距离100km,速度约为300m/s,基本匀速飞行,但受空气扰动影响,扰动加速度为零均值白噪声,方差强度 ;(2)雷达观测频率2Hz,观测误差为零均值白噪声,均方差为50m。
注意,这里给的量测噪声是均方差而非方差,这里我错了好多次。如果题目给的是均方差的话,那么建立量测噪声序列的时候就不用开平方,用代码来解释的话就是
R = 50; % 量测噪声
V = R*randn(1,T);
如果题目给的是方差的话,那么代码需要写成
R = 50;
V = sqrt(R)*randn(1,T)
第一题
【题目】
试采用信息滤波进行估计,初始信息阵取为0,与常规KF结果比较。
【解】
常规KF的原理公式默认已经掌握,这里不再给出,信息滤波的公式如下。
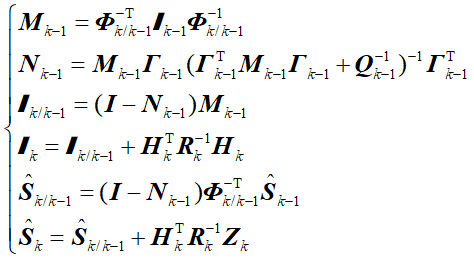
最后的输出如下
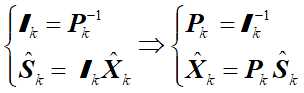
写成Matlab代码为
%% 04-1 习题1:信息滤波
if strcmp(mode, 'Problem 1')
% 分配空间并赋予滤波器变量初值
sIF = zeros(nS,T); % 信息滤波状态值
xIF = zeros(nS,T);
sIF(:,1) = I0*xState(:,1); % 信息滤波器赋估计初值
Phi_inv = pinv(Phi); % 先求逆,减少计算量
Q_inv = 1/Q;
R_inv = 1/R;
for t = 2:T
M_k_1 = Phi_inv' * I0 * Phi_inv;
N_k_1 = M_k_1 * Gamma * pinv(Gamma'*M_k_1*Gamma + Q_inv) * Gamma';
S_pre = (I - N_k_1)*Phi_inv'*sIF(:,t-1);
I_pre = (I - N_k_1)*M_k_1;
sIF(:,t) = S_pre + H'*R_inv*zMea(:,t);
I0 = I_pre + H'*R_inv*H;
xIF(:,t) = pinv(I0)*sIF(:,t);
end
% 画图
filerPlot(xState, zMea, xKF, xIF, 0, 0, 0, T, mode)
end
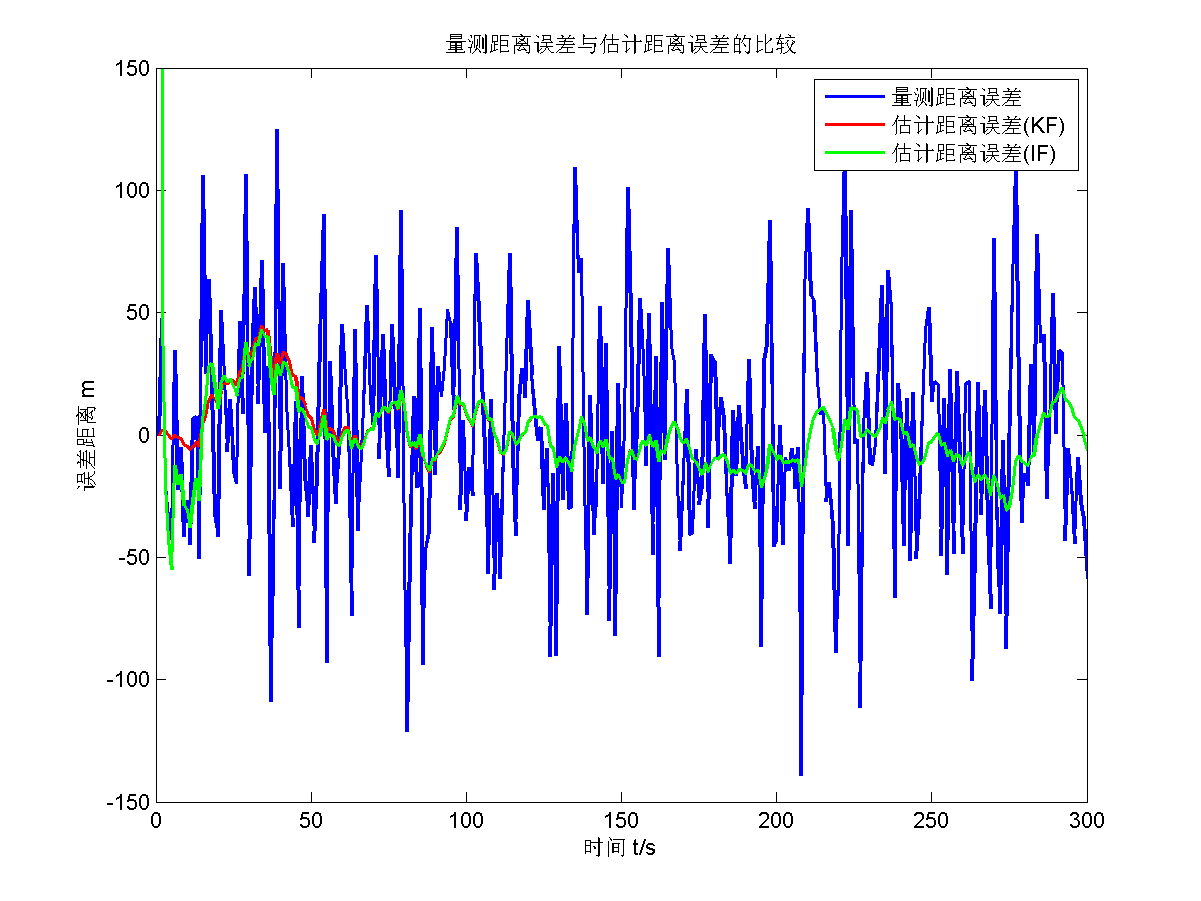
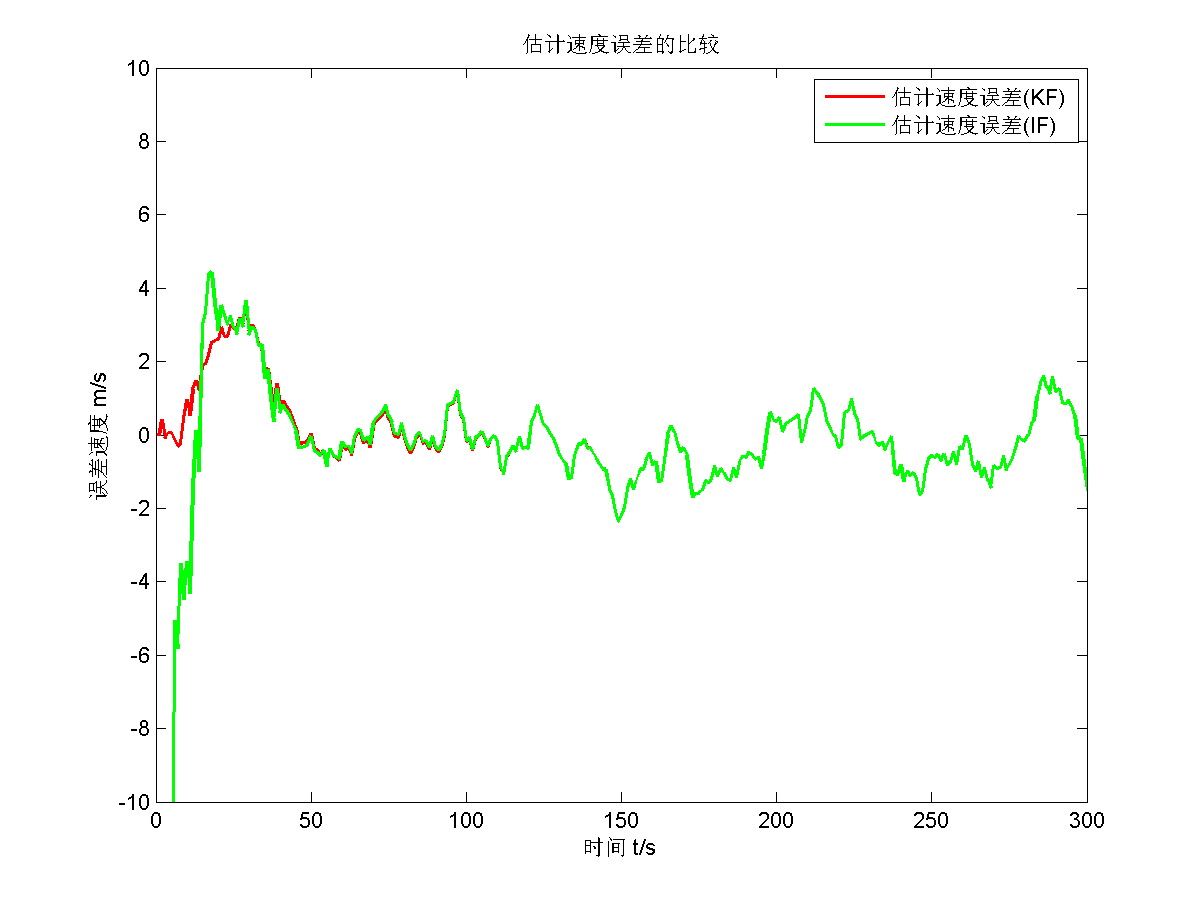
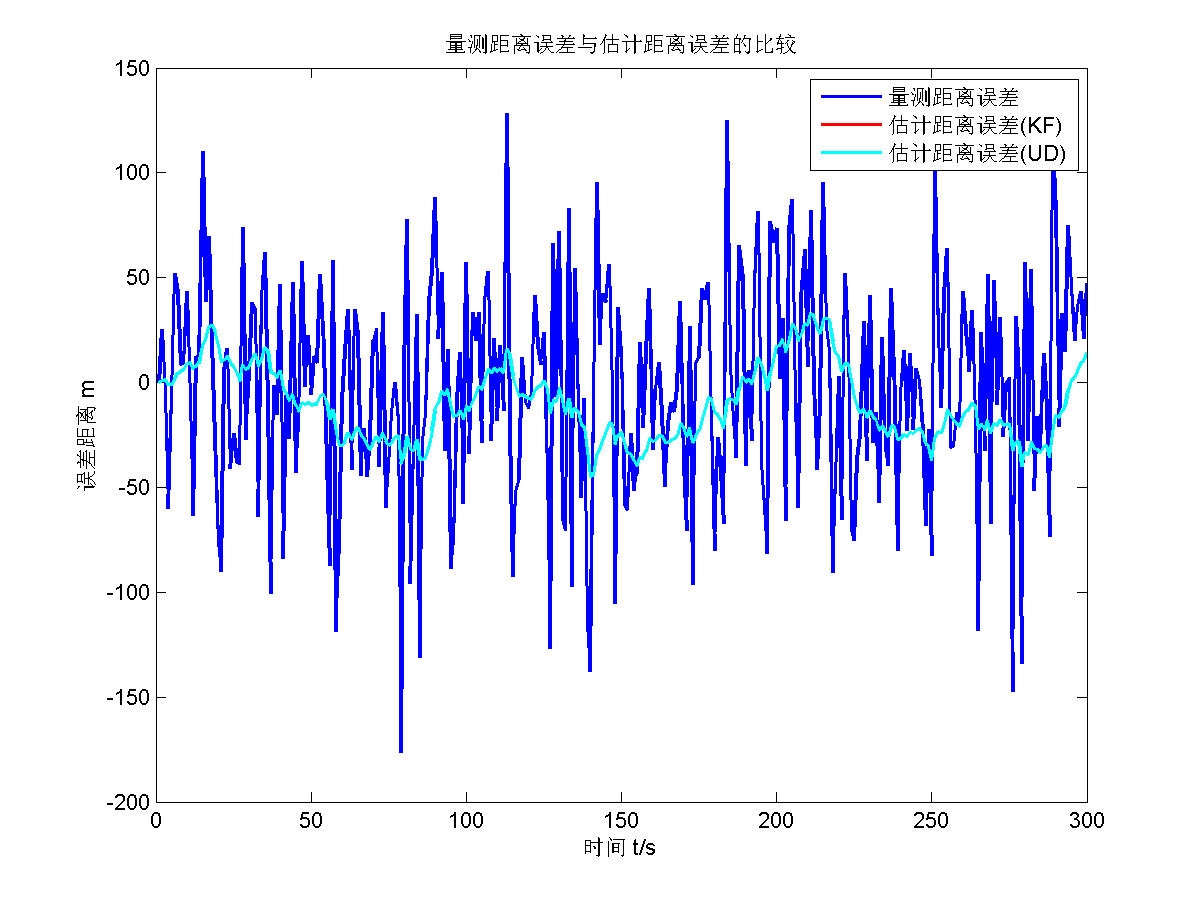
仿真结果如下面五张图所示。
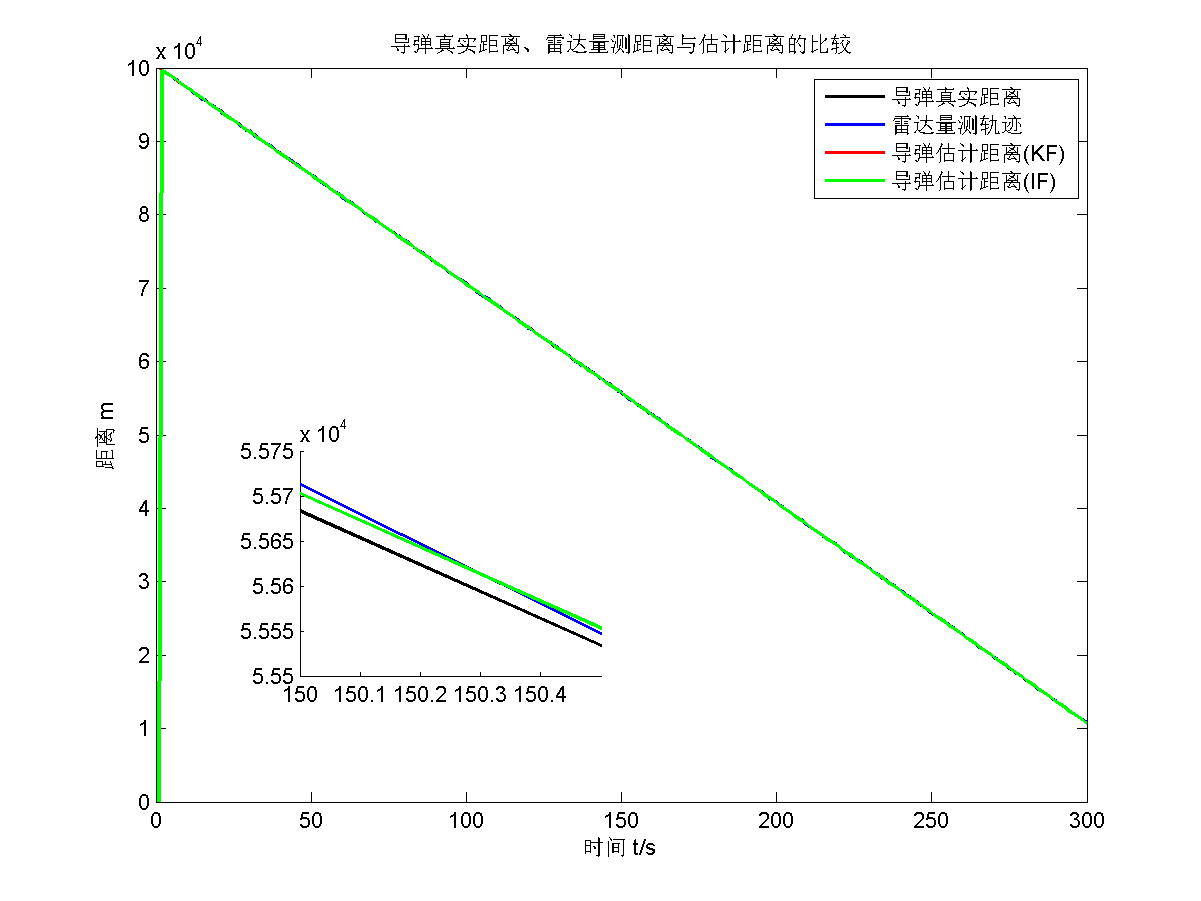
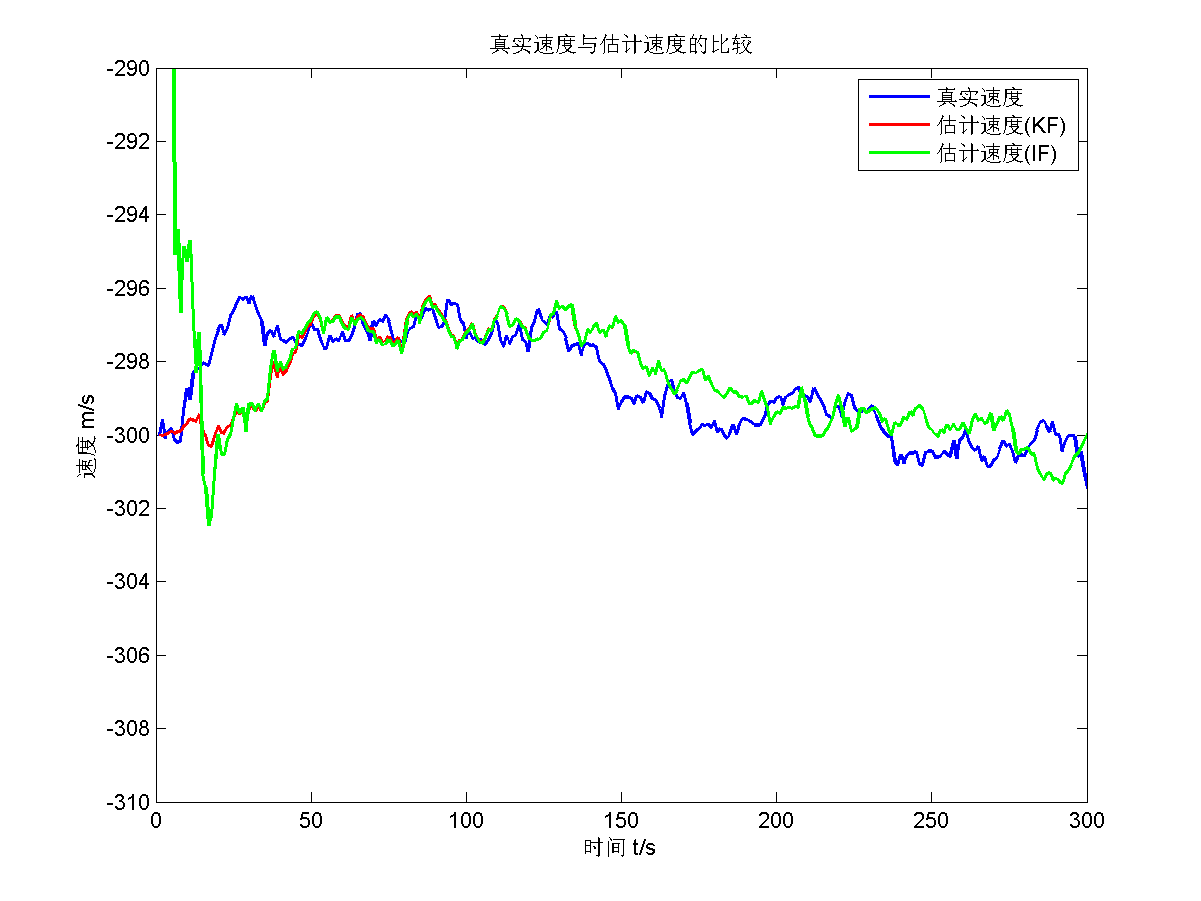
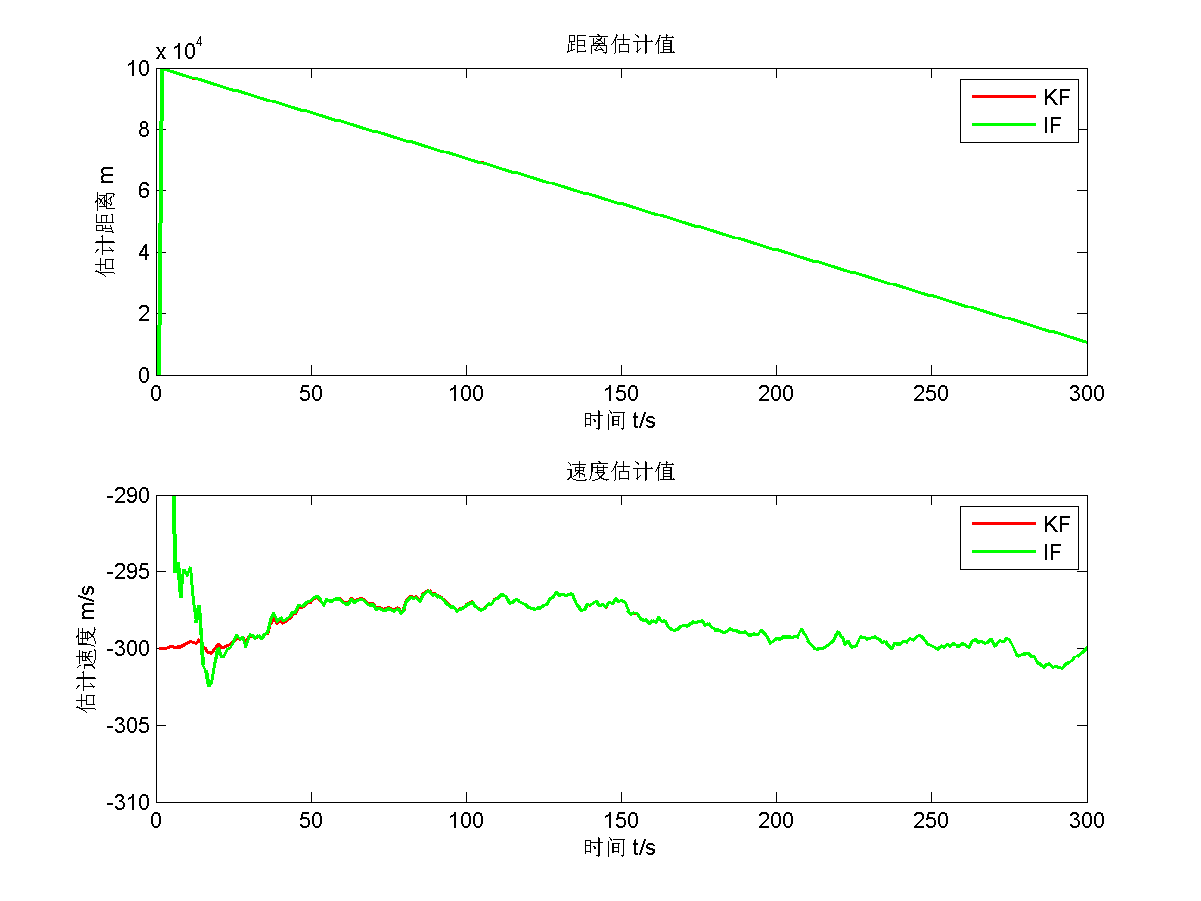
第二题
【题目】
试采用UD滤波进行估计,与常规KF结果比较。
【解】
这里没有什么好说的,就是在滤波过程中的协方差更新时,记得将协方差分解成ud矩阵就好。即 \(P_0=UDU^\mathrm{T}\) 其中,$D$ 是对角阵,$U$ 是三角阵。
直接上代码。
%% 04-2 习题2:UD滤波
if strcmp(mode, 'Problem 2')
% 分配空间并赋予滤波器变量初值
xUD = zeros(nS,T); % UD滤波状态值
xUD(:,1) = xState(:,1); % UD滤波器赋估计初值
%注意!!!这里一定要再给一次 P0,不然这里的初始 P0 就是 KF 结束后的值了。
P0 = diag([10^2,1^2]); % 初始协方差阵
for t = 2:T
% [xUD(:,t), P0] = UDKF(xUD, P0, zMea, Phi, Gamma, H, Q, R, t);
% 时间更新
xUD_pre = Phi*xUD(:,t-1);
[U, D] = udu(P0); % 将协方差阵作UD分解
[U, D] = UD_update(U, D, Phi, Gamma, Q, H, R, 'T'); % 将U和D进行时间更新,“T”意为Time update
P_pre = U*diag(D)*U';
% 量测更新
K = P_pre*H'*pinv(H*P_pre*H'+R);
xUD(:,t) = xUD_pre+ K*(zMea(:,t)-H*xUD_pre);
[U, D] = udu(P_pre); % 将一步预测协方差阵作UD分解
[U, D] = UD_update(U, D, Phi, Gamma, Q, H, R, 'M'); % 将U和D进行时间更新,“M”意为Measurement update
P0 = U*diag(D)*U';
end
% 画图
filerPlot(xState, zMea, xKF, 0, xUD, 0, 0, T, mode)
end
可以看到,时间更新和量测更新都是三步:
- 将误差协方差阵分解成U阵和D阵;
- 利用Bierman算法进行时间/量测更新,得到新的U阵和D阵;
- 再根据公式 $P_0=UDU^\mathrm{T}$ 更新一步预测误差协方差阵。
不过上课的时候,老师说,下面两行可以不要,换一个形式写,减少计算量。
第一行代码
P_pre = U*diag(D)*U';
这行求P_pre是为了计算后面的卡尔曼滤波增益K,但是可以使用其他计算K的公式来规避P_pre 的出现。
第二行代码
[U, D] = udu(P_pre); % 将一步预测协方差阵作UD分解
这里不需要再做UD分解了,直接使用时间更新好的UD矩阵即可。
然后给出UD滤波的仿真结果。
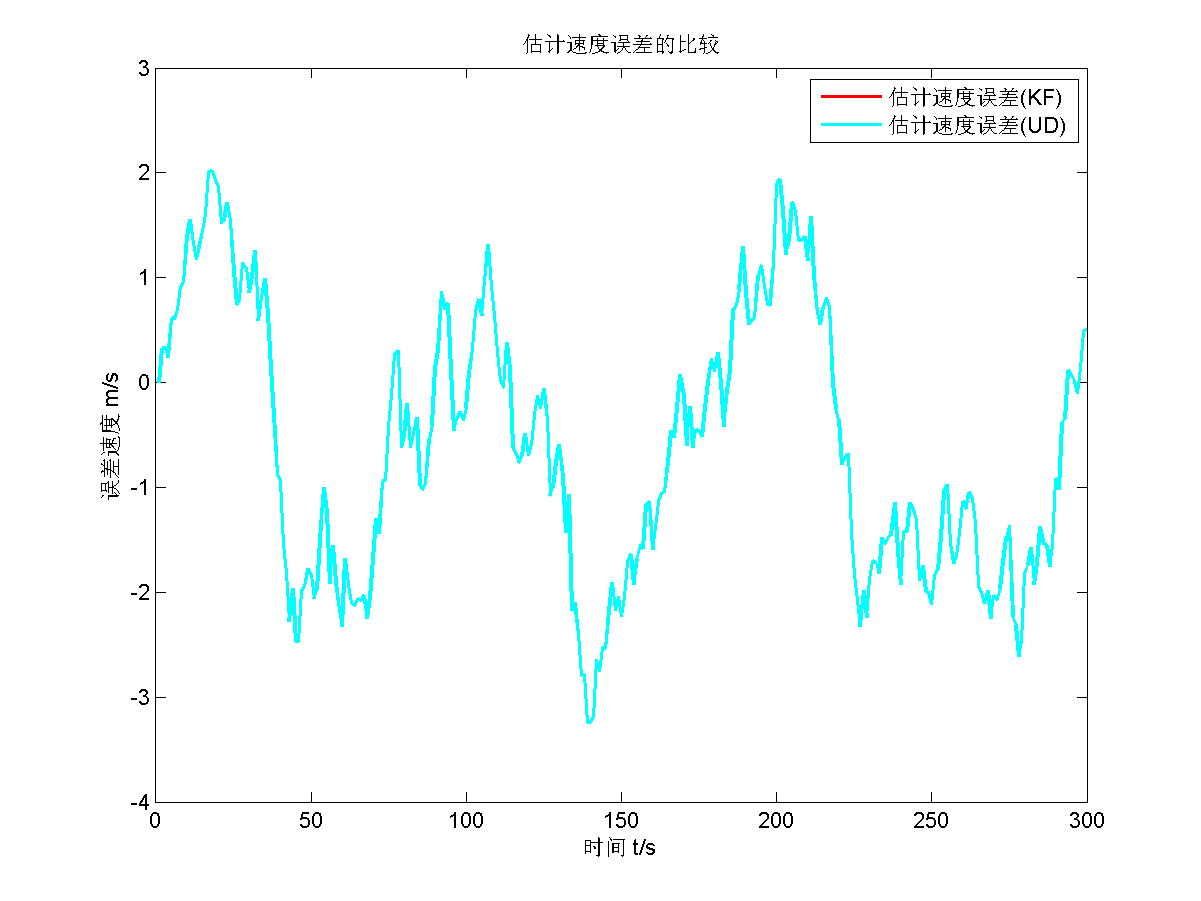
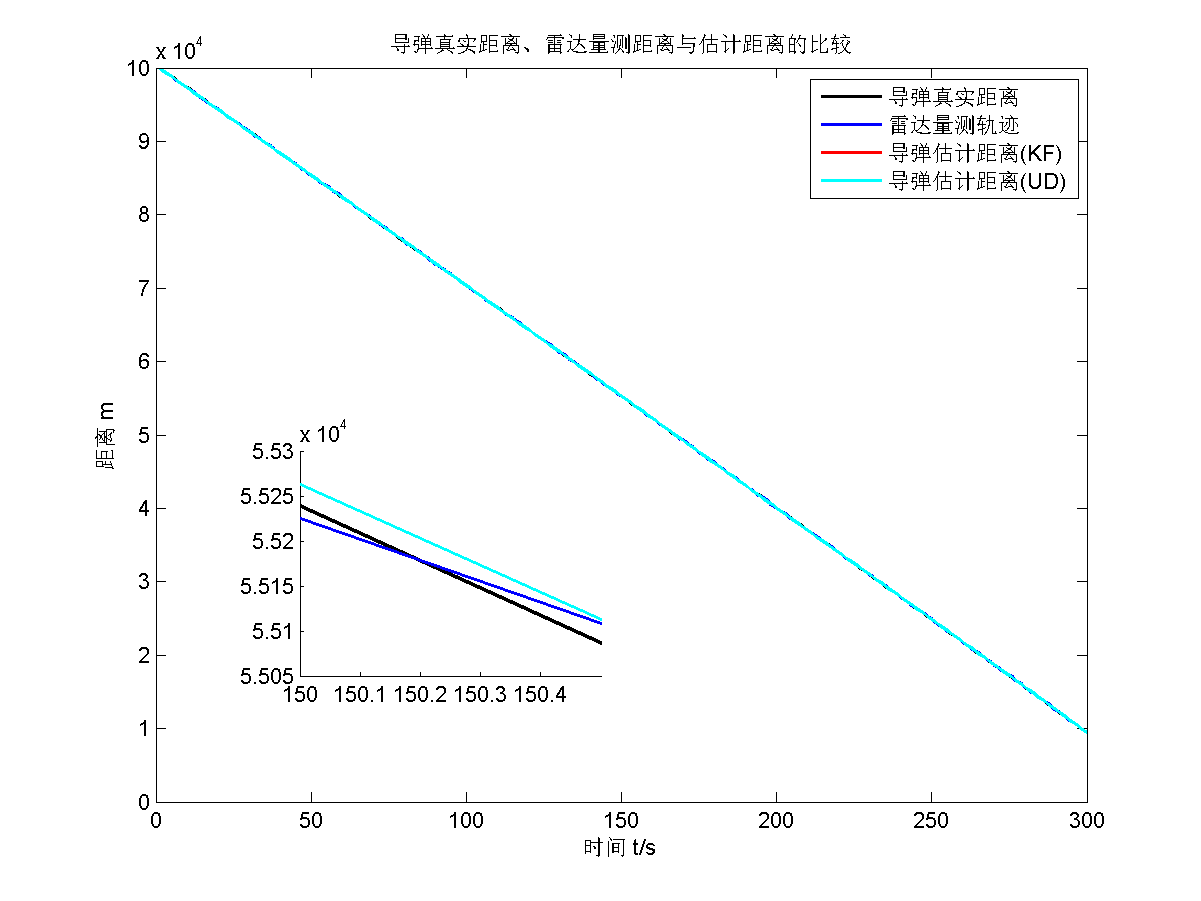
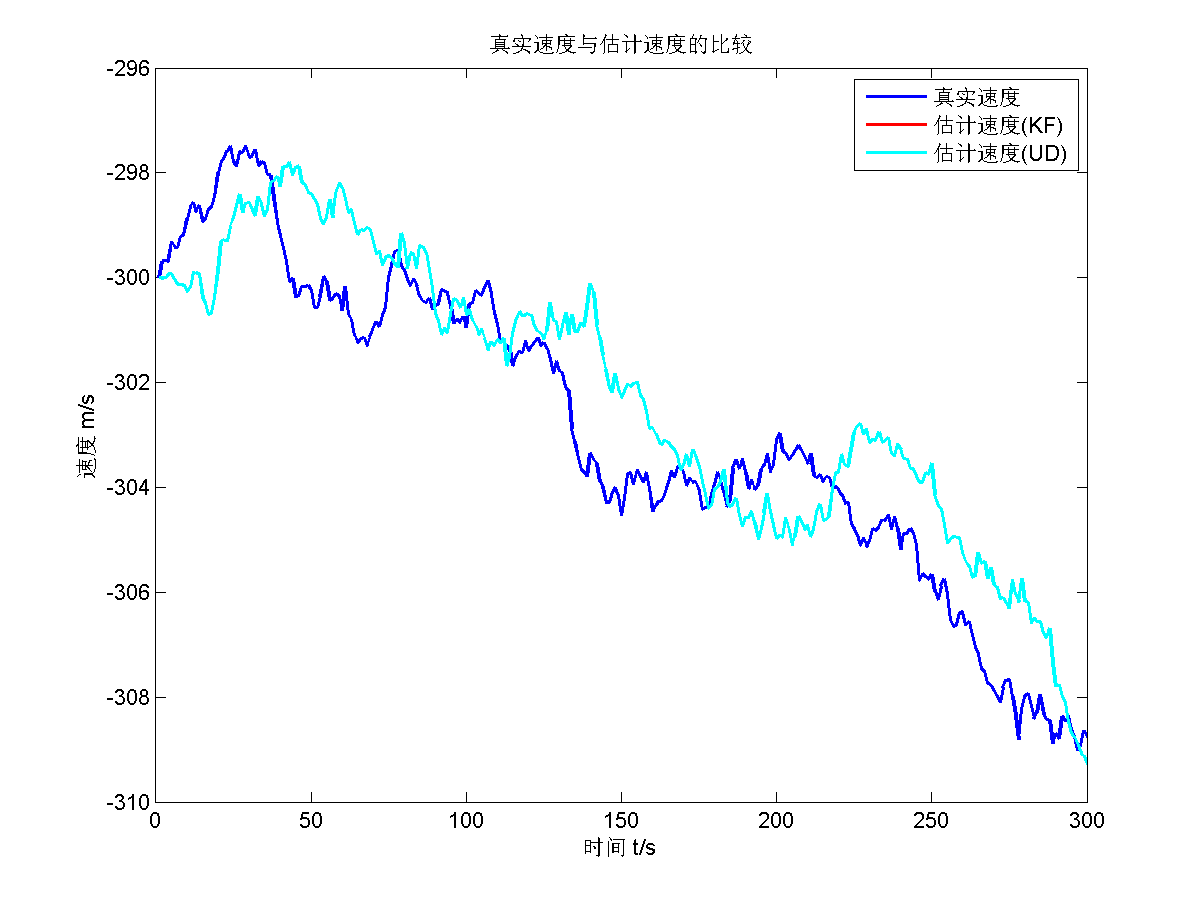
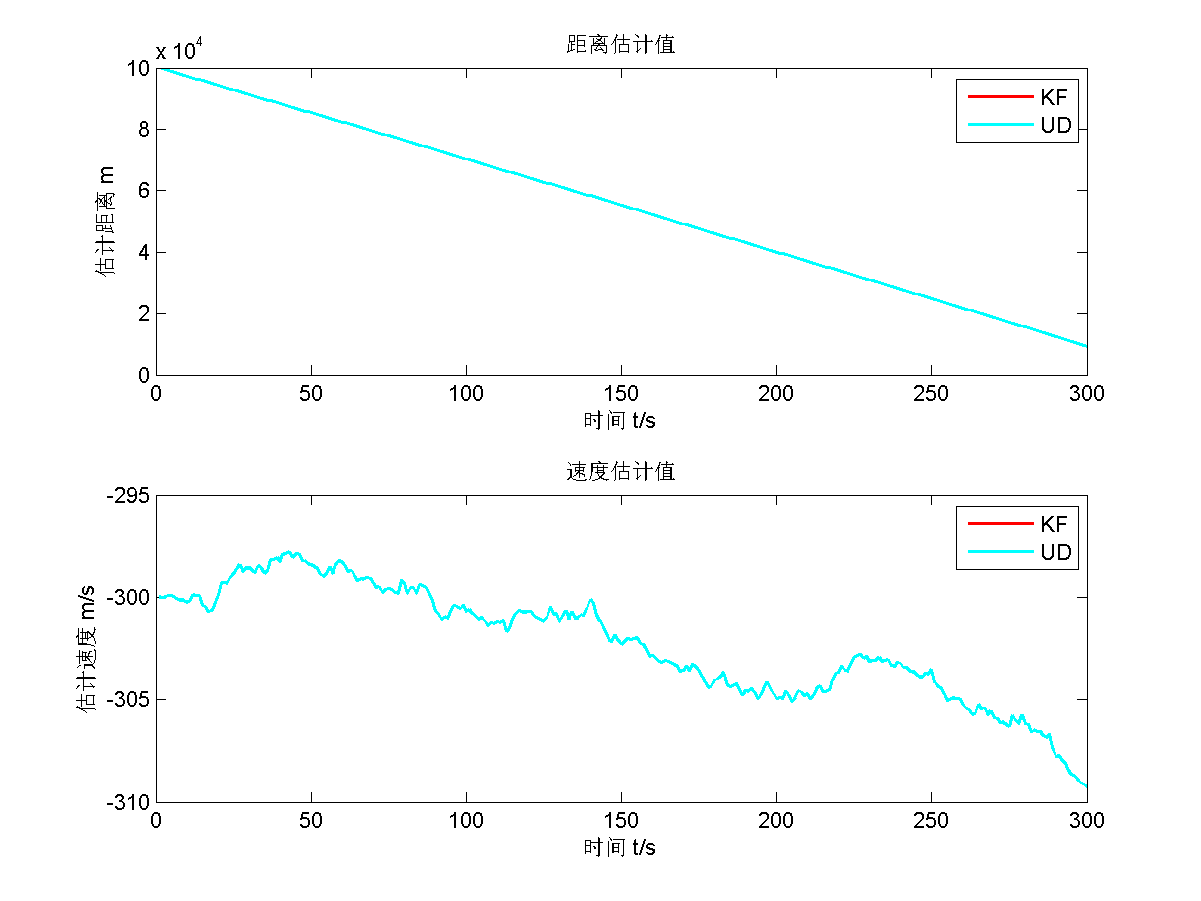
UD滤波的估计值应该与KF的估计值趋势是一摸一样的,没有半点差别,因为只是把误差协方差阵 $P_0$ 进行了UD分解,数值上保持不变。所以估计值的趋势和值的大小是一摸一样的。而且估计值比真实值慢一拍这个趋势也是正常的,在“真实速度与估计速度”这张图中有体现。
第三题
【题目】
假设导弹在100-200$\mathrm{s}$存在 $-1 \ \mathrm{m/s^2}$减速机动,即在200$\mathrm{s}$时速度大小减为约200$\mathrm{m/s}$,之后继续匀速向前飞行,然而整个飞行过程中测量雷达仍认为导弹是匀速的并建成匀速模型。试使用遗忘滤波进行滤波估计,并与常规KF估计效果比较。
【解】
这里需要注意的是“整个飞行过程中测量雷达仍认为导弹是匀速的并建成匀速模型”。一开始我理解为量测模型是错的,一直在量测导弹匀速飞行时候的位置了。但不是的,这句话意思表达不清楚,其实可以不看,整个题目就是正常地量测导弹位置即可,不用考虑太多。
原理公式如下图所示。
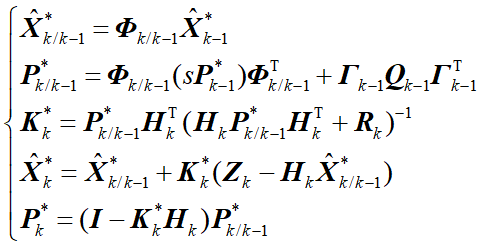
比较卡尔曼滤波的原理公式可知,遗忘滤波与传统卡尔曼滤波公式的区别就是在一步预测误差协方差阵的时候,多加了一个渐消因子 $s$。
注意,一般渐消因子 $s$在1.1到1.3附近,不能取太大了,取太大了估计效果不好。下面分别给出渐消因子 $s=1.3$ 和渐消因子 $s=10$的估计结果。
给出Matlab代码
%% 04-3 习题3:遗忘滤波
if strcmp(mode, 'Problem 3')
% 根据题设条件,设置初始化参数
a = 1; % 加速度(m/s^2),减速机动,因为速度为负,所以这里符号为正
acc = [0.5*Ts^2;Ts]*a; % 构造矩阵
t_100 = 100; % 时间(s),导弹在第100秒时,减速机动
t_200 = 200; % 时间(s),导弹在第200秒后,停止减速机动,进入匀速运动
% 根据题设条件,用模型模拟真实状态
% 因为假定测量雷达仍认为导弹是匀速飞行,并建成匀速模型
% 故此处仍使用在代码第02节生成的量测数据 zMea
for t = 2:T
if t < t_100 || t >= t_200
xState(:,t) = Phi*xState(:,t-1) + Gamma*W(:,t);
elseif t >= t_100 && t < t_200
xState(:,t) = Phi*xState(:,t-1) + acc + Gamma*W(:,t);
end
zMea(:,t) = H*xState(:,t) + V(t);
end
% 分配空间并赋予滤波器变量初值
s = 1.1; % 渐消因子
xKF = zeros(nS,T); % 卡尔曼滤波状态值
xKF(:,1) = xState(:,1); % 卡尔曼滤波器估计初值
xFD = zeros(nS,T); % 遗忘滤波状态值
xFD(:,1) = xState(:,1); % 遗忘滤波器赋估计初值
% 再做一次卡尔曼滤波,先前第03-1节的卡尔曼滤波作废,因为 xState 发生变化了
for t = 2:T
[xKF(:,t), P0] = KF(xKF, P0, zMea, Phi, Gamma, H, Q, R, I, t);
end
% 遗忘滤波
% 因为上一步进行了卡尔曼滤波,P0的值发生了变化,因此需重新赋值一次
P0 = diag([10^2,1^2]); % 初始协方差阵
for t = 2:T
% 时间更新
xFD_pre = Phi*xFD(:,t-1);
P_pre = Phi*s*P0*Phi' + Gamma*Q*Gamma';
% 量测更新
K = P_pre*H'*pinv(H*P_pre*H'+R);
xFD(:,t) = xFD_pre+ K*(zMea(:,t)-H*xFD_pre);
P0 = (eye(2)-K*H)*P_pre;
end
% 画图
filerPlot(xState, zMea, xKF, 0, 0, xFD, 0, T, mode)
end
首先给出渐消因子 $s=1.3$的估计结果。
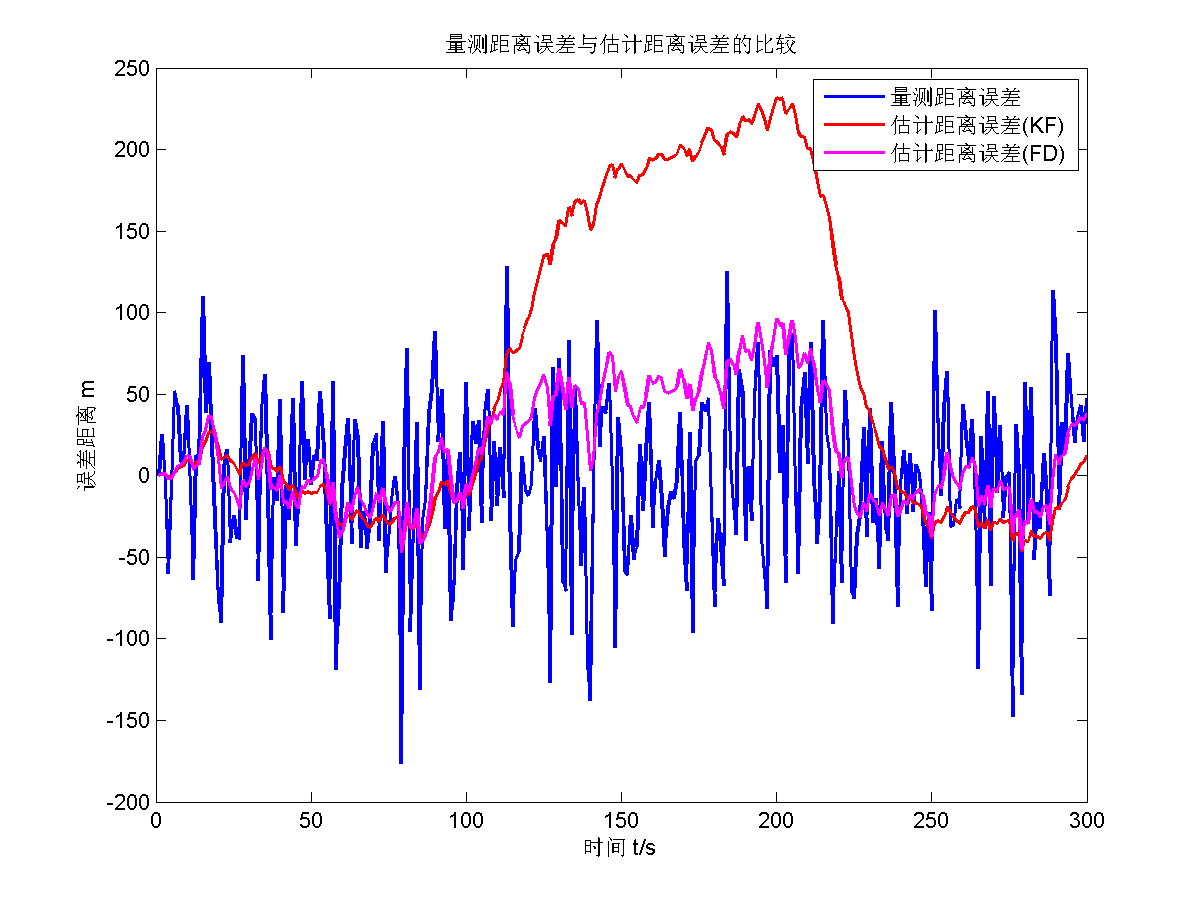
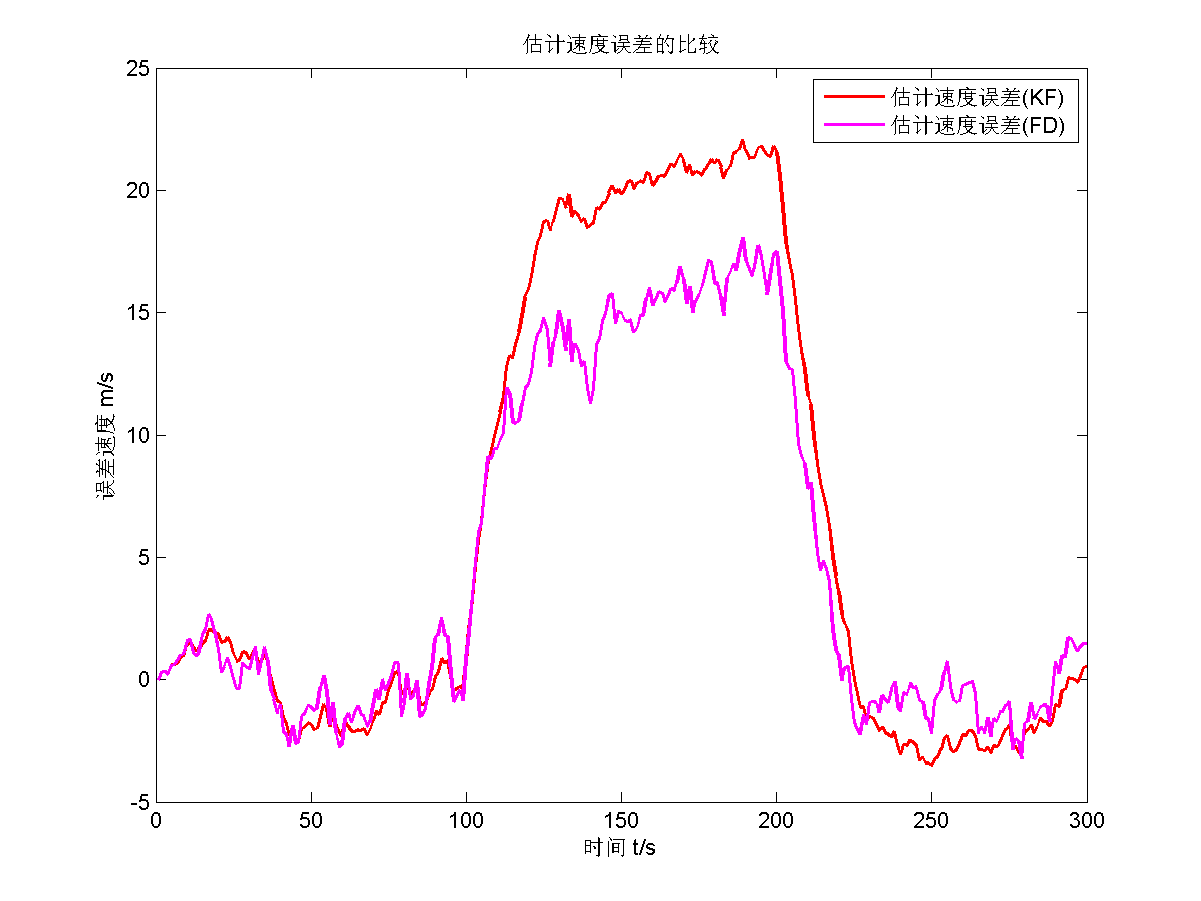
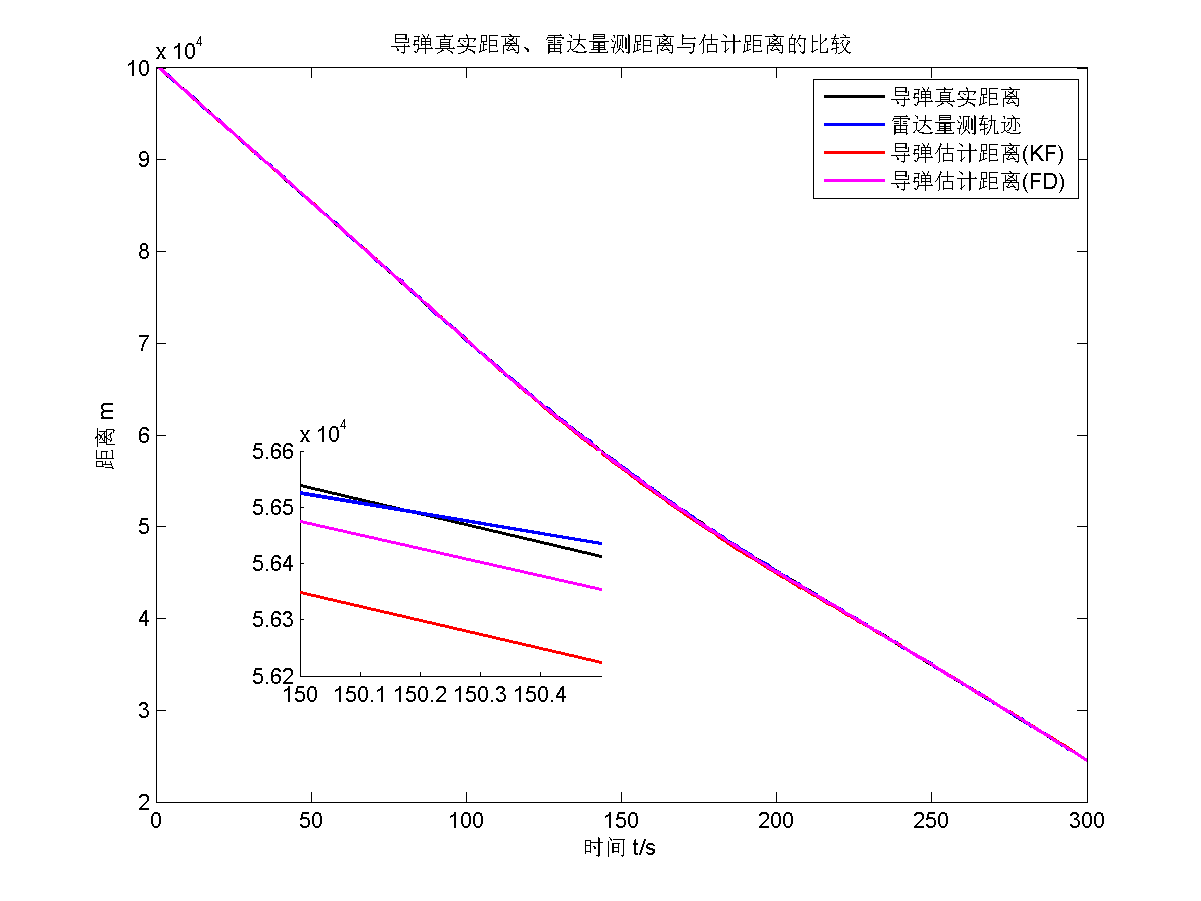
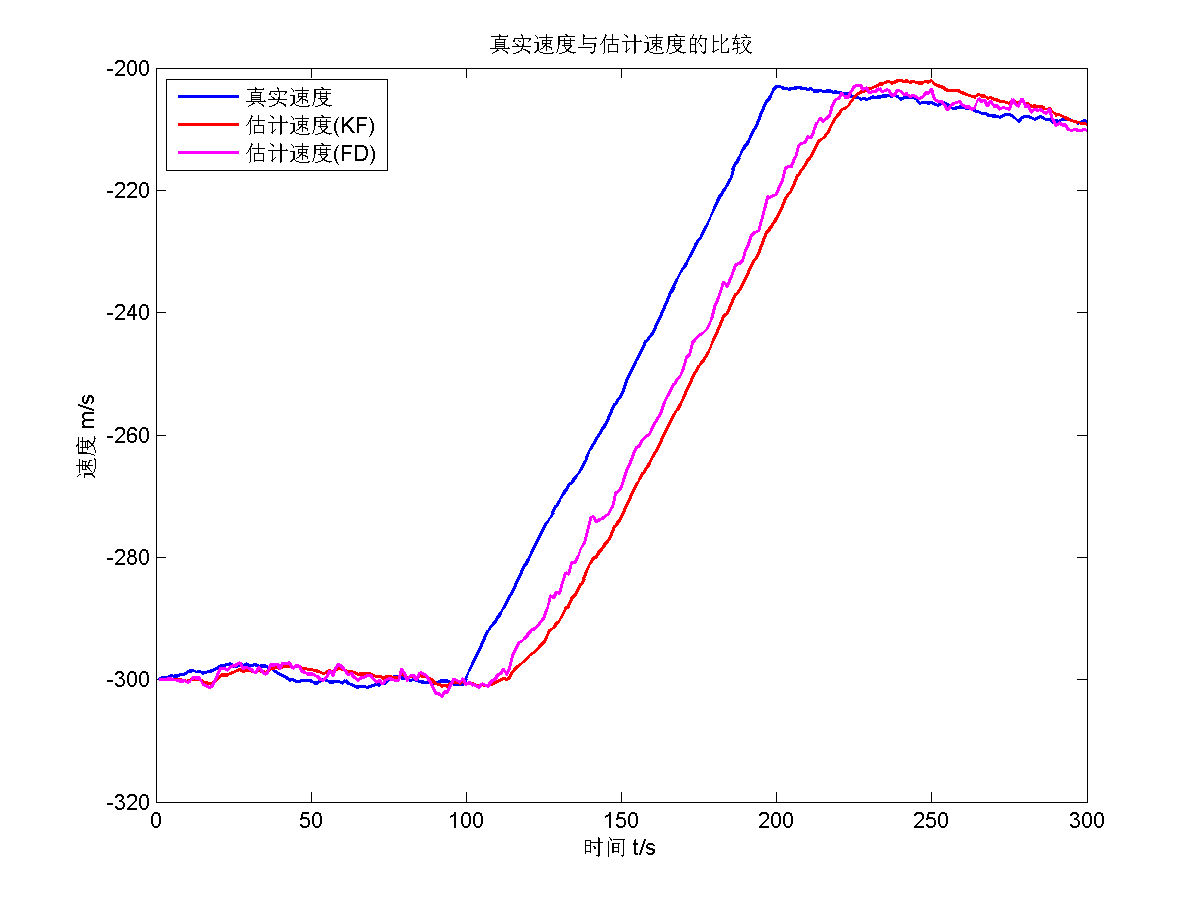
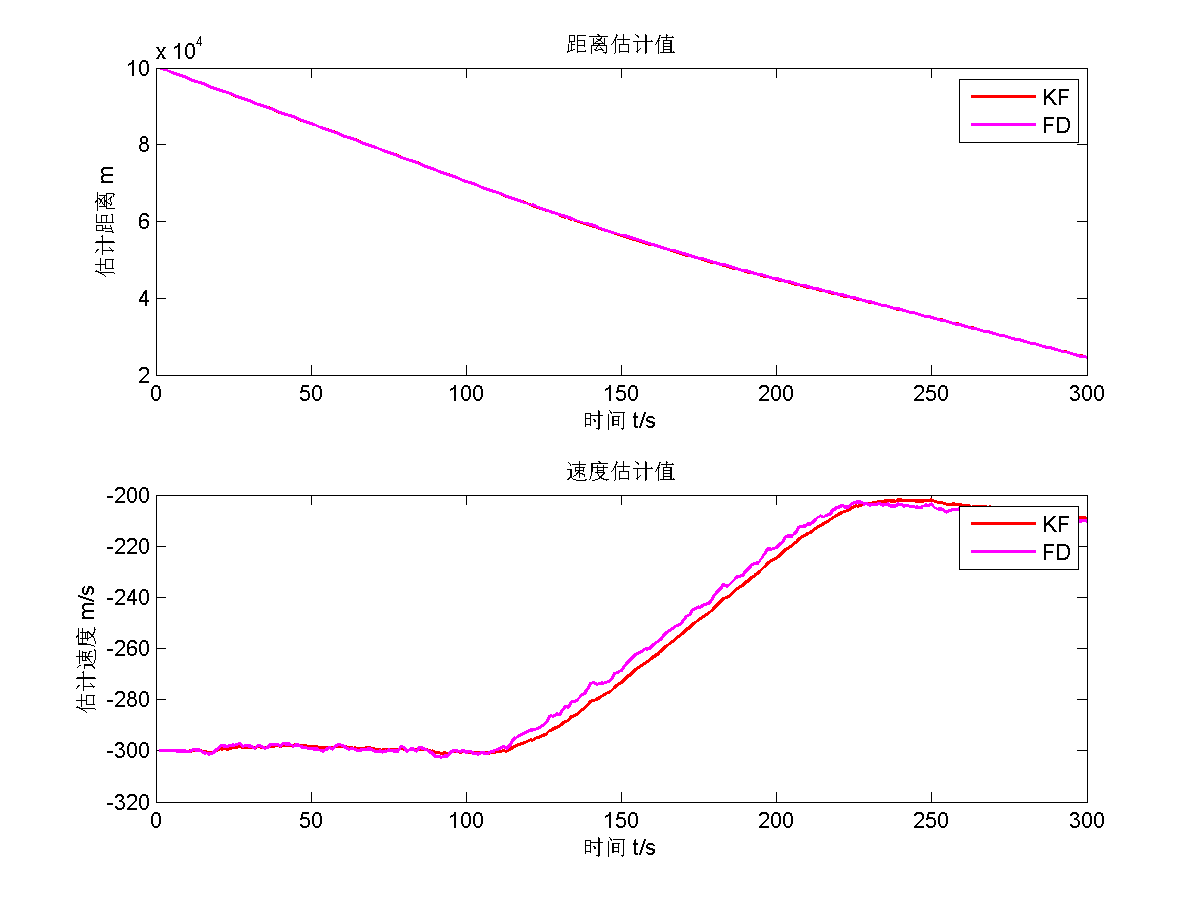
可以看出来,估计效果不错,而且在因为模型不准确,遗忘滤波的估计效果要比传统KF估计效果更好。
【注意】
如果模型建得很准确的话,遗忘滤波的估计效果反而比传统KF的估计效果差。
再给出渐消因子 $s=10$的估计结果。
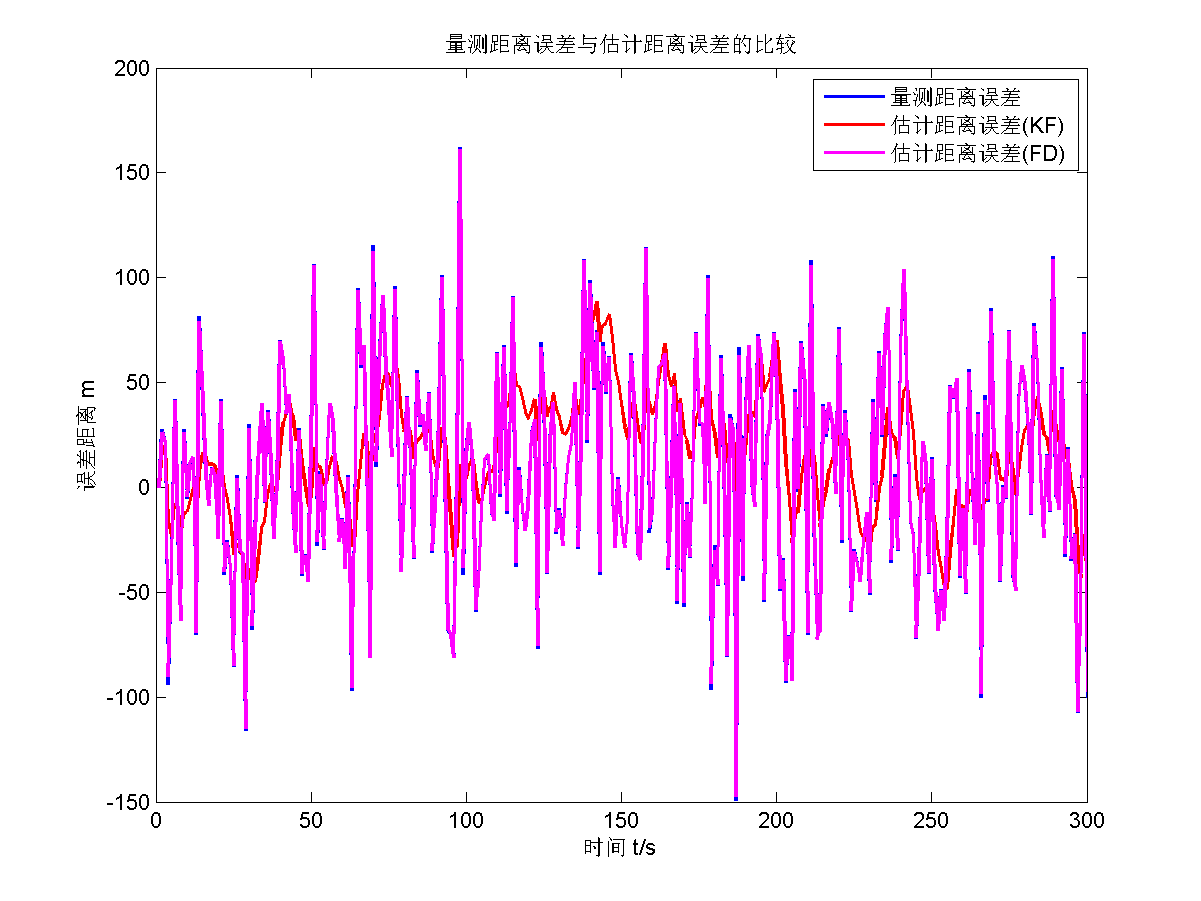
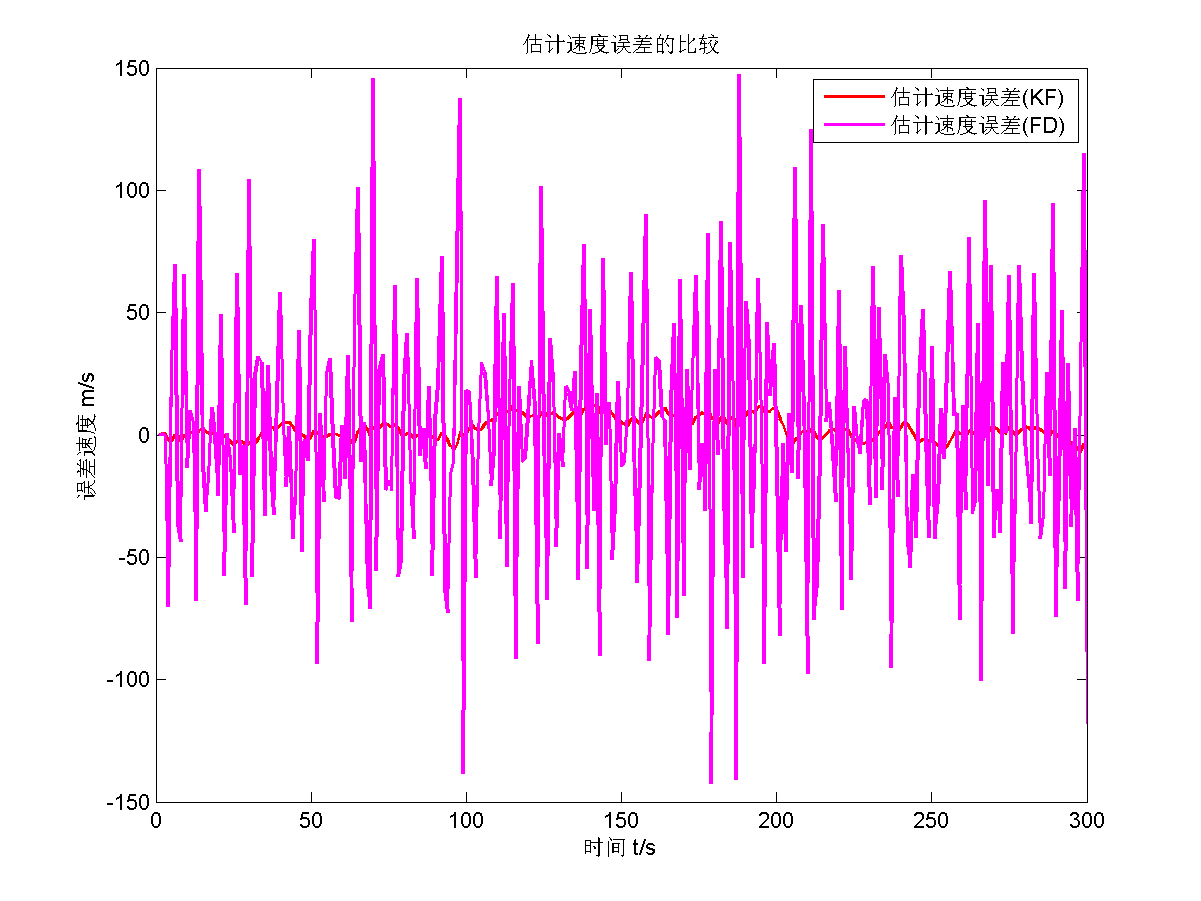
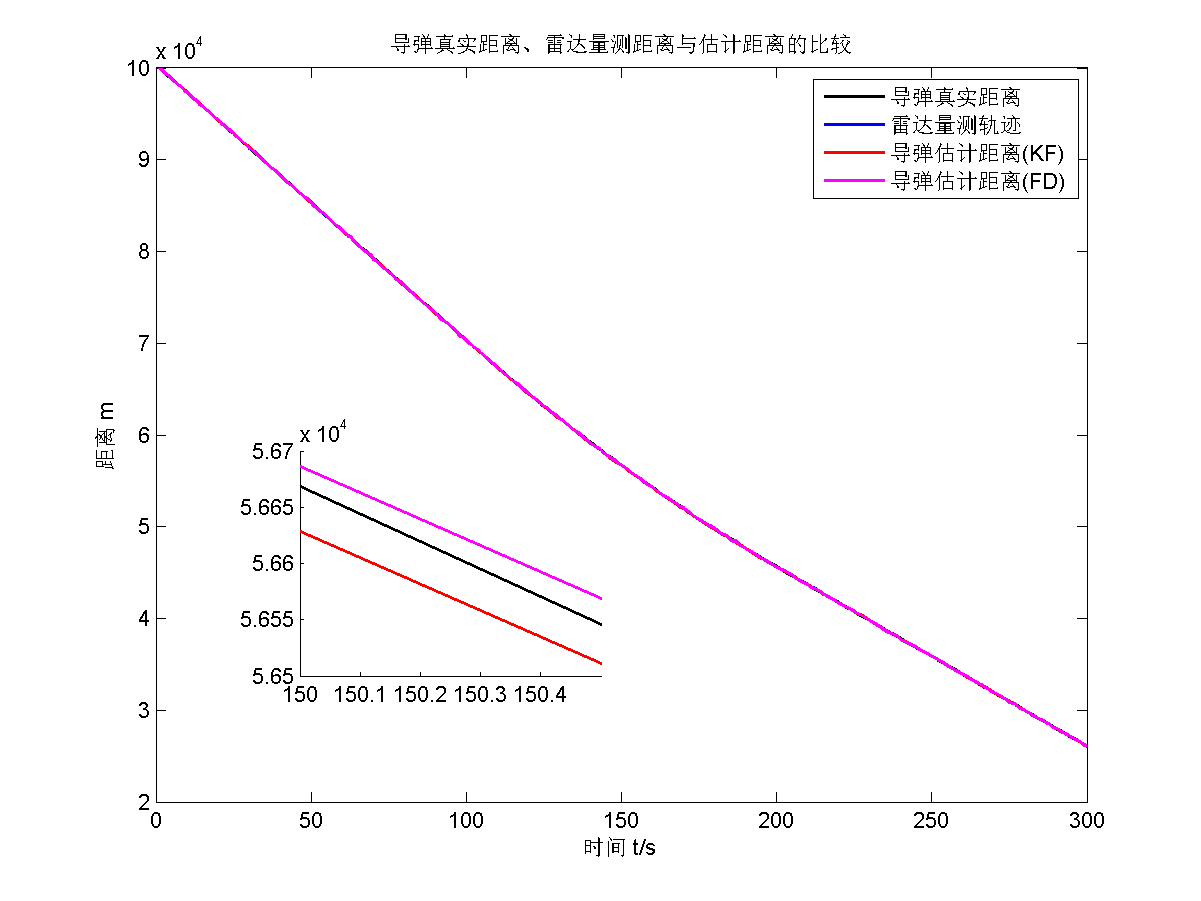
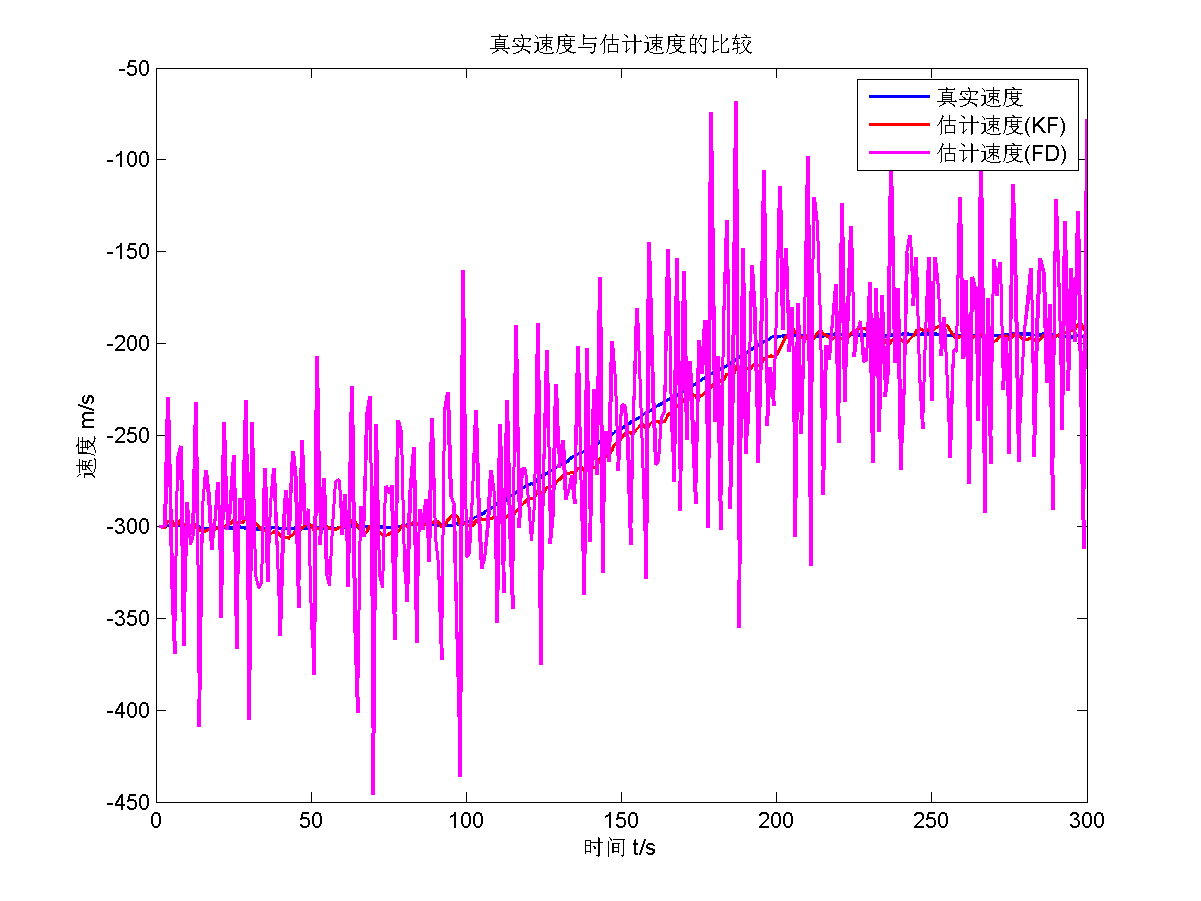
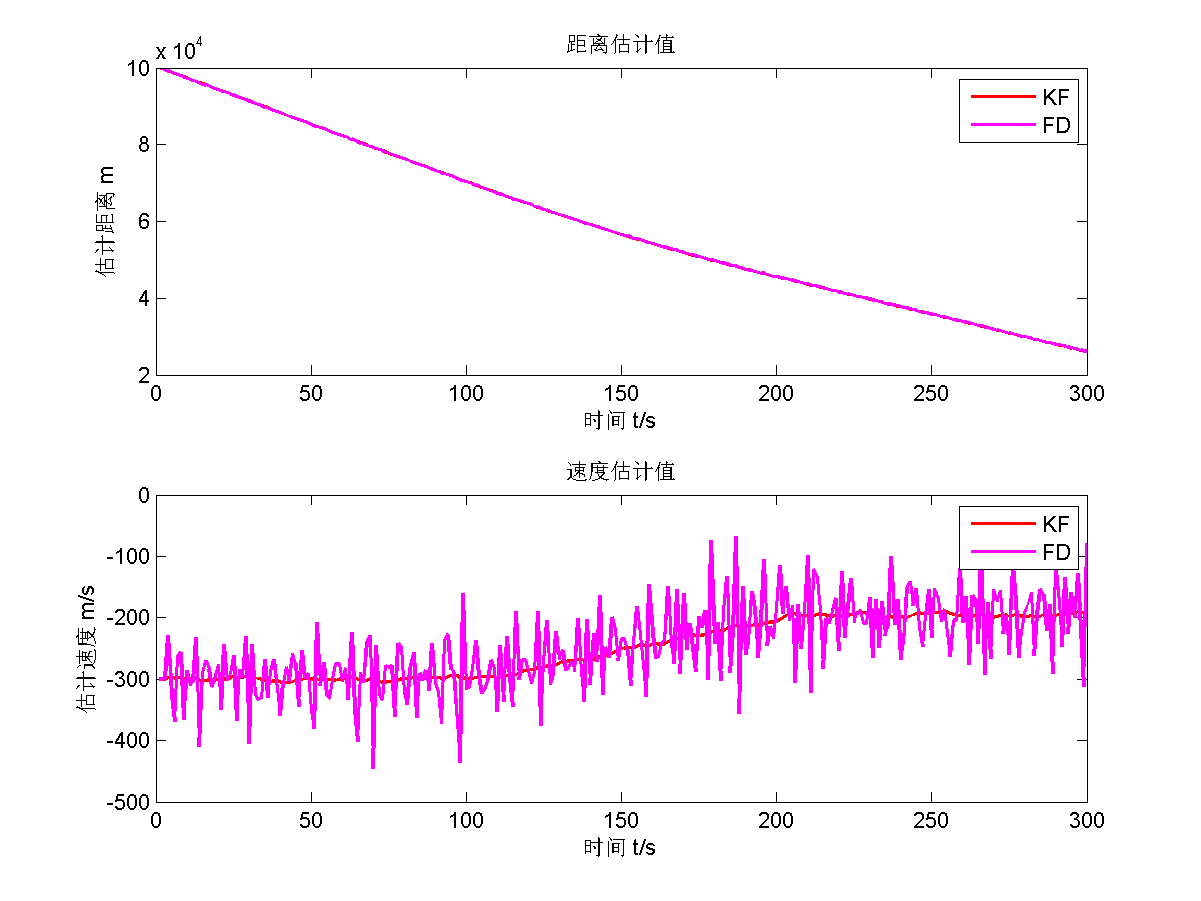
因为渐消因子取得太大了,估计效果不好,而且十分震荡,精度很差,稳定性不好。所以遗忘滤波的渐消因子不能取得过大。
第四题
【题目1】
(1)第一种情况,1-100s方差为100 $\mathrm{m^2}$,100s之后为10000 $\mathrm{m^2}$,并且在150s时雷达出现一次量测故障使雷达输出为0;
【解】
注意,在滤波过程中,KF和自适应滤波的R阵不用变!!!用最开始的R阵就可,无论后面的量测噪声方差怎么变,滤波过程中的R都不改变!!!
下面给出自适应滤波的原理公式,首先给出新息序列方差阵的求法。 \(\hat{C}_k=(1-\beta_k)\hat C_{k-1}+\beta_k\tilde Z_{k/k-1}\tilde Z_{k/k-1}^\mathrm{T}\) $\tilde{Z}_{k/k-1}^\mathrm{T}$ 为估计器的新息。
$\beta_k$ 的计算公式如下。 \(\beta_k = \frac{\beta_{k-1}}{\beta_{k-1}+b}\\ \beta_0 = 1,\ \beta_\infty =1-b,\ 0<b<1\) 一般来说,b的取值很靠近1,建议取值有 $b=0.9$、$b=0.99$、$b=0.999$ 或者是其他取值。
1)量测故障的检测与隔离
用下面的公式来判断 \(\mathrm{tr}(\hat C_k) \gg \mathrm{tr}(H_kR_{k/k-1}H_k^{\mathrm{T}}+R_k)\) $H_k$ 是量测矩阵, $R_k$ 是量测噪声。这些都是KF的量。这些矩阵本来应该是都是要加粗的,但是我用LaTex写加粗斜体显得代码太长了,就不写了。(稍微缺失一点严谨性)
Matlab代码为
C = (1-beta(t))*C + beta(t)*(zNew*zNew');
abs(trace(C)/trace(H*P_pre*H'+R_1s)) > 2
下面这行代码右边的数字2可以按经验选择其他的数字。
如果上式判断公式成立的话,就不需要量测更新,直接时间更新了。因为量测偏差这么大,用量测值来更新没有意义,更加不准,还不如就用估计预测值预测下一步的状态更加准确一些。
2)量测方差自适应滤波
用下面的公式来实现,其实就是改变量测噪声。 \(\alpha_kR_k \approx \hat C_k-H_kP_{k/k-1}H_k^\mathrm {T} \\ \alpha_k=\frac{\mathrm{tr}(\hat C_k-H_kP_{k/k-1}H_k^\mathrm {T})}{\mathrm{tr}(R_k)}\) 注意,这里除了 $\alpha_k$ 之外,其他的量都要加粗。
Matlab代码为
alpha = trace(C-H*P_pre*H')/trace(R_1s);
K = P_pre*H'*pinv(H*P_pre*H'+alpha*R_1s);
介绍了量测故障的检测与隔离和量测方差自适应滤波后,给出整个自适应滤波的代码。
%% 04-4-1 习题4(1)
if strcmp(mode, 'Problem 4-1')
R_1s = 100; % 量测噪声方差为100m^2
R_100s = 10000; % 量测噪声方差为10000m^2
% 构造量测噪声序列,此处单位是方差,故需开方
V(1:100) = sqrt(R_1s)*randn(1,100); % 1-100s,方差为100m^2
V(101:T) = sqrt(R_100s)*randn(1,(T-100)); % 100s之后,方差为10000m^2
% 根据题设条件,用模型模拟真实状态
for t = 2:T
if t == 150 % 在150s时出现量测故障导致雷达输出为0
zMea(:,t) = 0;
else
zMea(:,t) = H*xState(:,t) + V(t);
end
end
% 再做一次卡尔曼滤波,先前第03-1节的卡尔曼滤波作废,因为 zMea 发生变化了
for t = 2:T
% 时间更新
xKF_pre = Phi*xKF(:,t-1);
P_pre = Phi*P0*Phi' + Gamma*Q*Gamma';
% 量测更新
K = P_pre*H'*pinv(H*P_pre*H'+R_1s);
xKF(:,t) = xKF_pre+ K*(zMea(:,t)-H*xKF_pre);
P0 = (eye(2)-K*H)*P_pre;
end
% 分配空间并赋予滤波器变量初值
xFault = zeros(nS,T); % 自适应遗忘滤波状态值
xFault(:,1) = xState(:,1); % 自适应遗忘滤波器赋估计初值
beta = zeros(1,T); beta(1) = 1;
b = 0.999; % 渐消因子
C = H*(Phi*P0*Phi' + Gamma*Q*Gamma')*H' + R;% 新息序列方差阵
zNew = 15;
% 量测噪声方差自适应滤波处理
for t = 2:T
% 时间更新
xFault_pre = Phi*xFault(:,t-1); % 状态一步预测
P_pre = Phi*P0*Phi' + Gamma*Q*Gamma'; % 协方差一步预测的中间步骤
% 量测更新
beta(t) = beta(t-1)/(beta(t-1)+b); % 更新新息序列方差阵的系数
C = (1-beta(t))*C + beta(t)*(zNew*zNew');
if abs(trace(C)/trace(H*P_pre*H'+R_1s)) > 2 % 量测故障检测与隔离
xFault(:,t) = xFault_pre; % 无需量测更新,估计值用时间更新值代替
P0 = P_pre;
else
alpha = trace(C-H*P_pre*H')/trace(R_1s);
K = P_pre*H'*pinv(H*P_pre*H'+alpha*R_1s);
zNew = zMea(:,t)-H*xFault_pre;
xFault(:,t) = xFault_pre+ K*zNew;
P0 = (eye(2)-K*H)*P_pre;
end
end
% 画图
filerPlot(xState, zMea, xKF, 0, 0, 0, xFault, T, mode)
end
zNew这个值我是根据程序实际情况设的zNew=15,一开始的 $C_0$ 我写成了 C = H*(Phi*P0*Phi'+Gamma*Q*Gamma')*H'+R,用于最开始时刻的量测故障判断。
仿真结果为
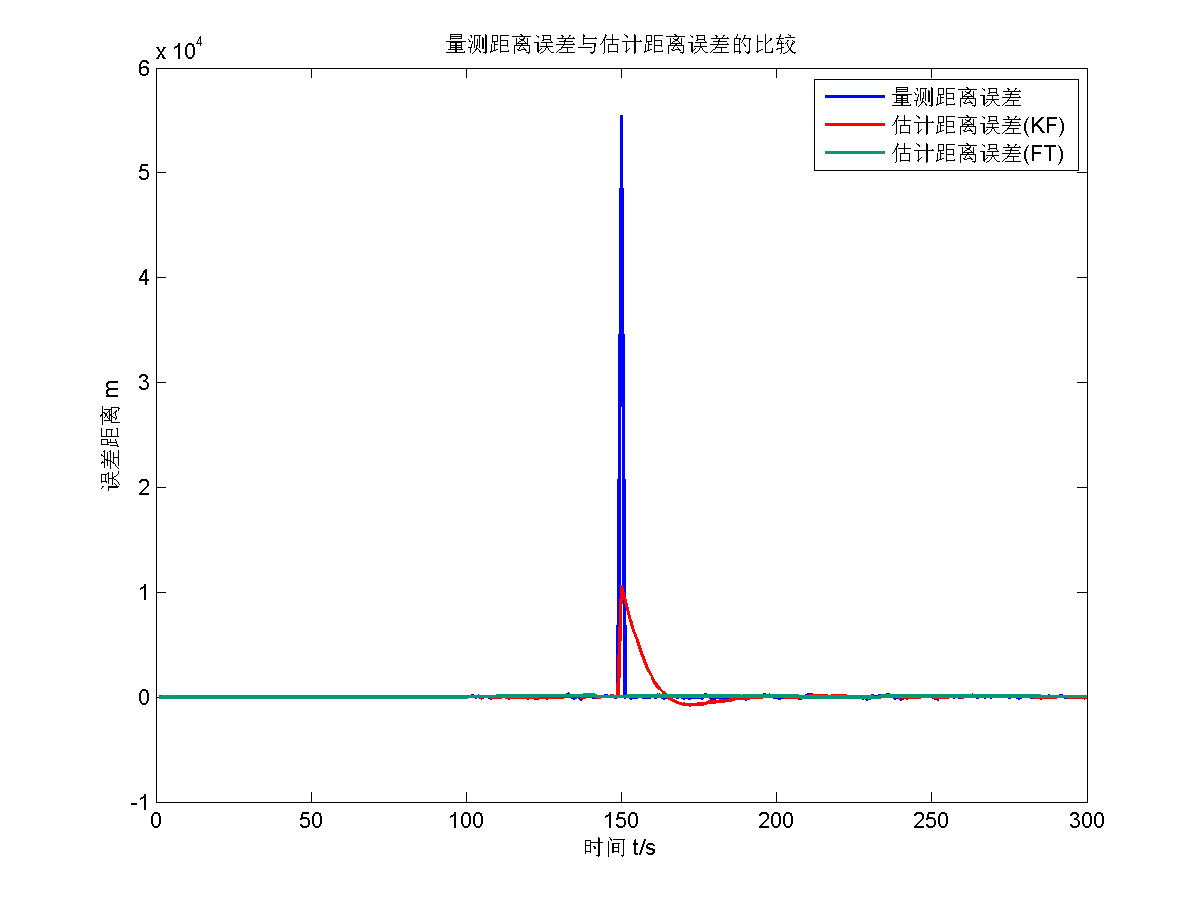
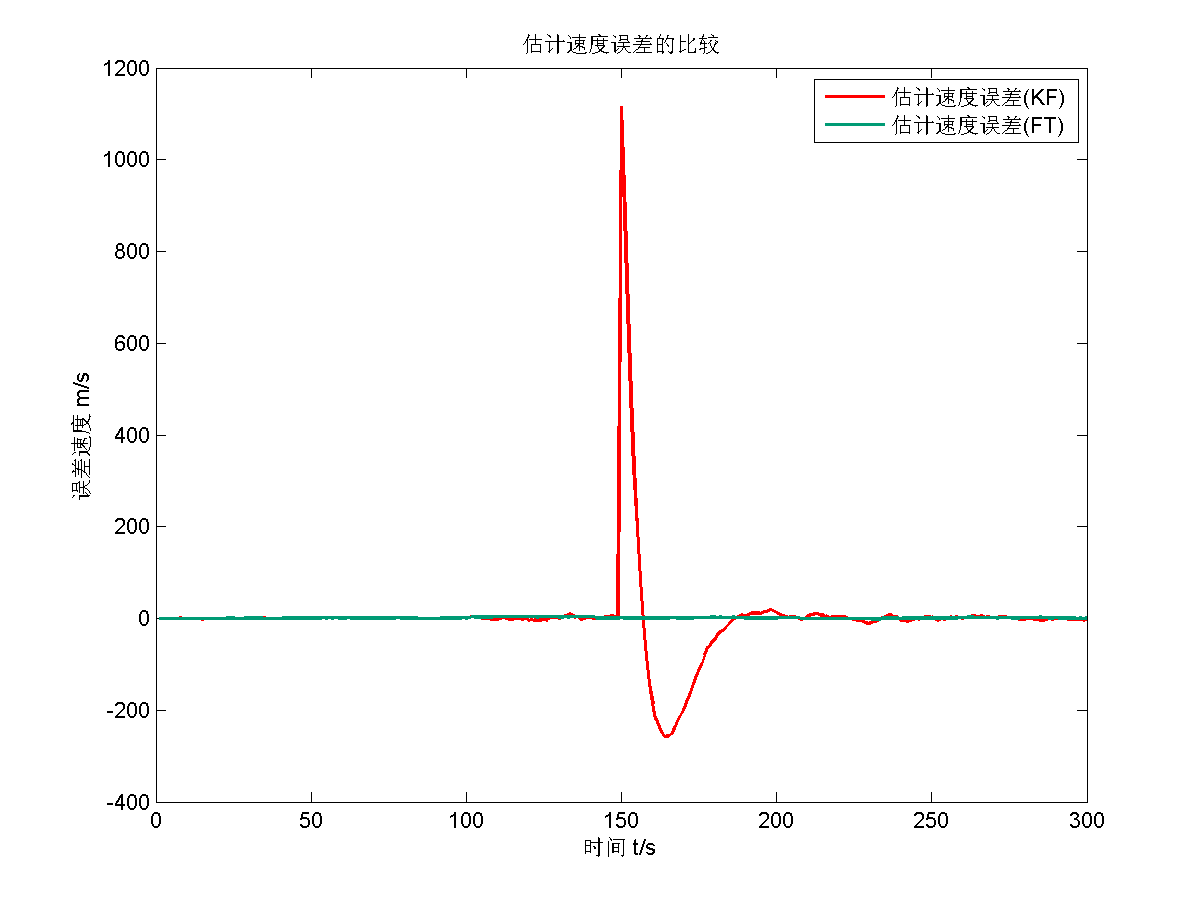
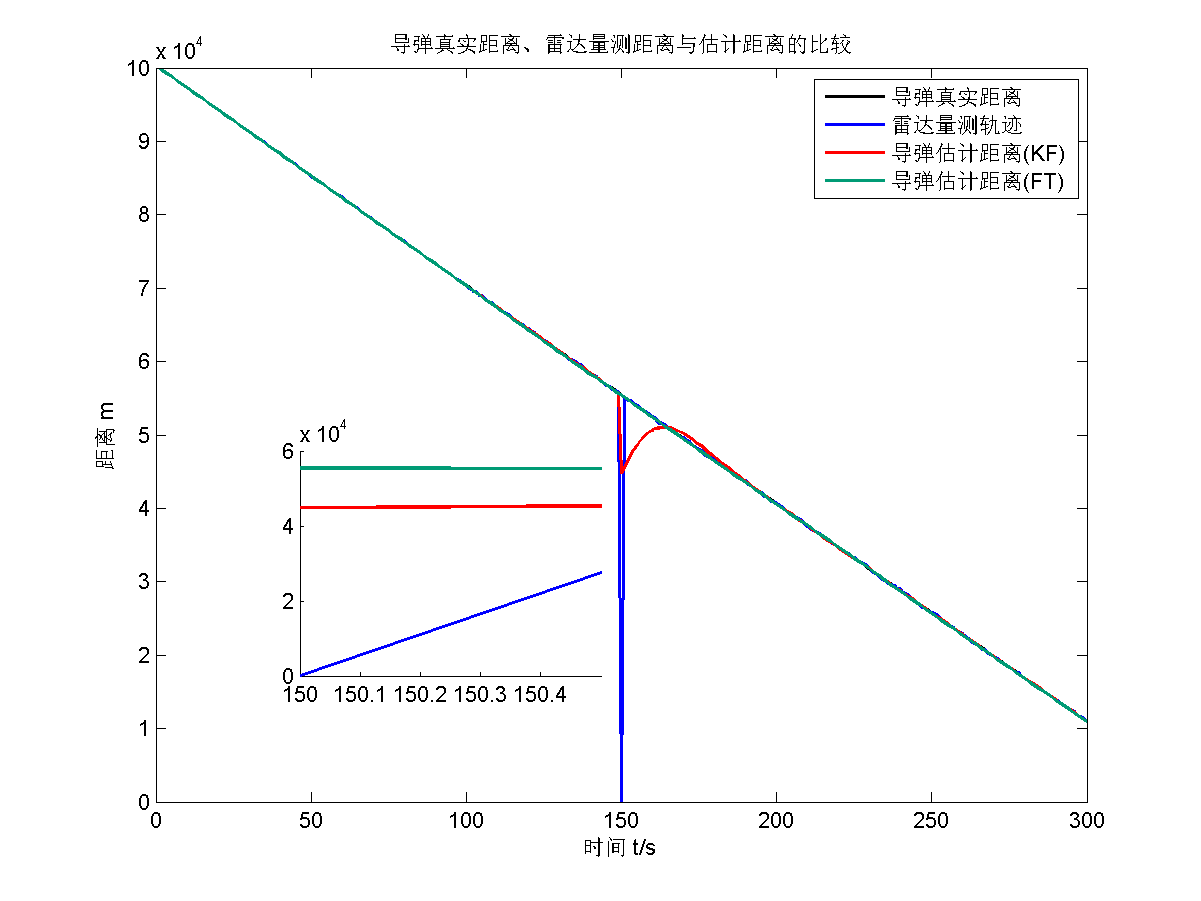
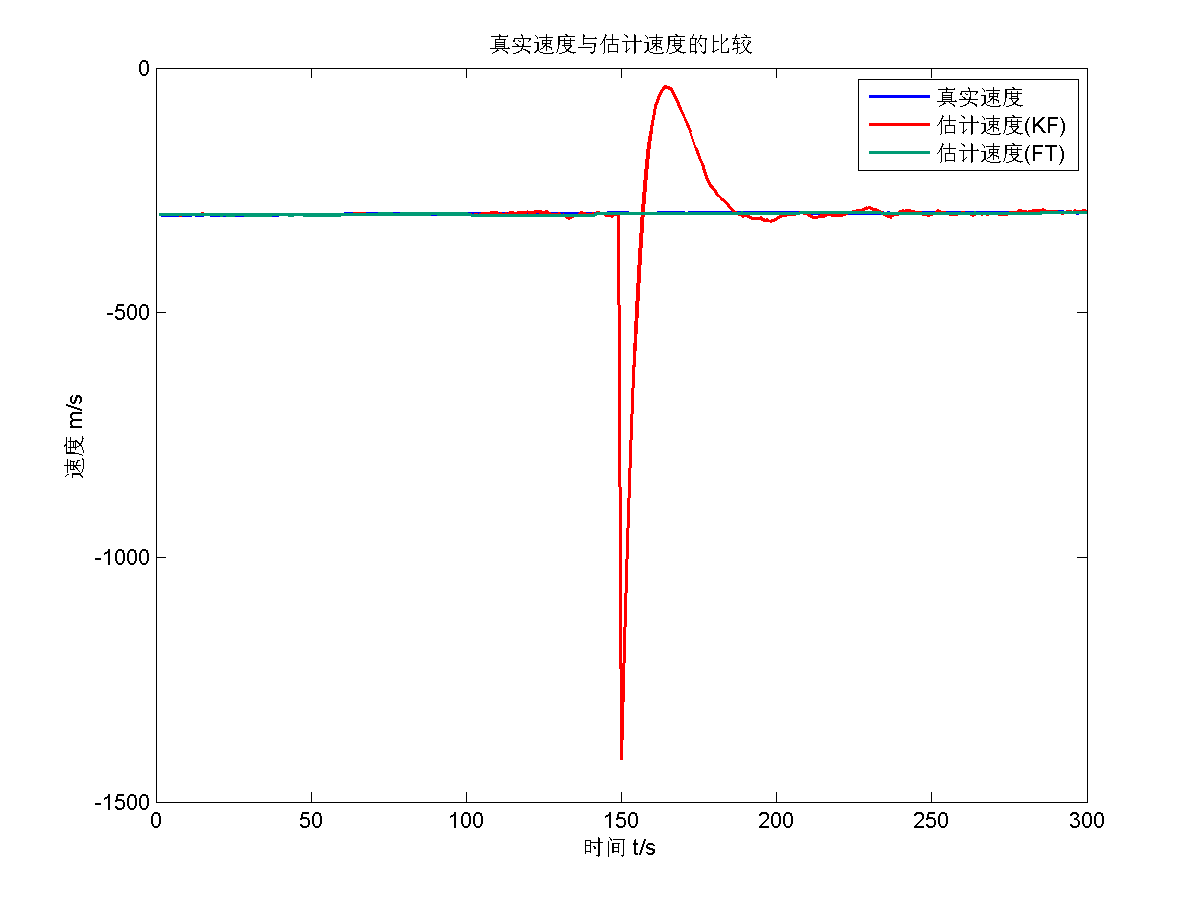
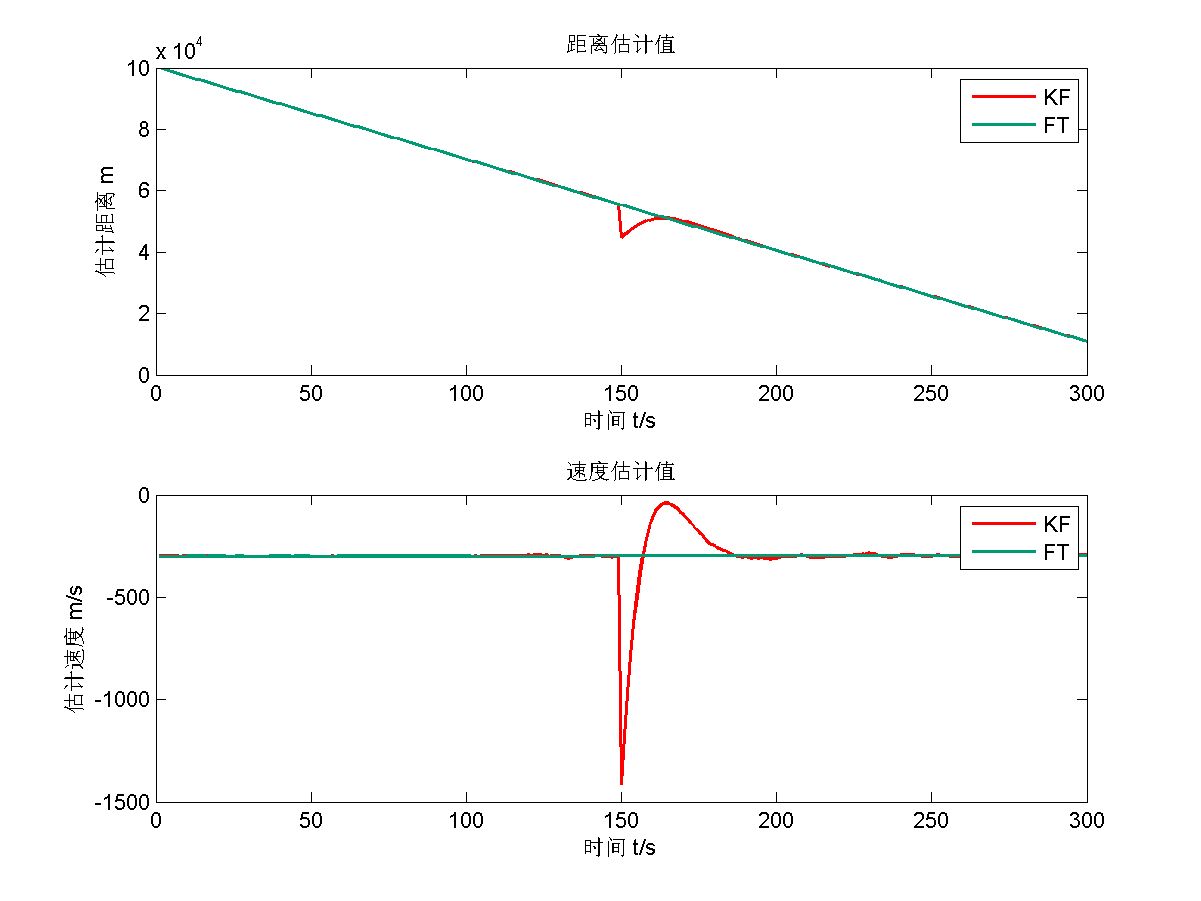
【题目2】
(2)第二种情况,1-100s方差为100 $\mathrm{m^2}$,100s之后为10 $\mathrm{m^2}$ 。分别对两种情况进行量测噪声方差自适应滤波处理,对比自适应滤波结果及常规KF的结果。
【解】
这里的处理不多说,和(1)一样,直接给代码。
%% 04-4-2 习题4(2)
if strcmp(mode, 'Problem 4-2')
R_1s = 100; % 量测噪声方差为100m^2
R_100s = 10; % 量测噪声方差为10m^2
% 构造量测噪声序列,此处单位是方差,故需开方
V(1:100) = sqrt(R_1s)*randn(1,100); % 1-100s,方差为100m^2
V(101:T) = sqrt(R_100s)*randn(1,(T-100)); % 100s之后,方差为10m^2
% 根据题设条件,用模型模拟真实状态
for t = 2:T
zMea(:,t) = H*xState(:,t) + V(t);
end
% 再做一次卡尔曼滤波,先前第03-1节的卡尔曼滤波作废,因为 zMea 发生变化了
for t = 2:T
% 时间更新
xKF_pre = Phi*xKF(:,t-1);
P_pre = Phi*P0*Phi' + Gamma*Q*Gamma';
% 量测更新
% 这里不要改变KF的R阵值
K = P_pre*H'*pinv(H*P_pre*H'+R_1s);
xKF(:,t) = xKF_pre+ K*(zMea(:,t)-H*xKF_pre);
P0 = (eye(2)-K*H)*P_pre;
end
% 分配空间并赋予滤波器变量初值
xFault = zeros(nS,T); % 自适应遗忘滤波状态值
xFault(:,1) = xState(:,1); % 自适应遗忘滤波器赋估计初值
beta = zeros(1,T); beta(1) = 1;
b = 0.999; % 渐消因子
C = H*(Phi*P0*Phi' + Gamma*Q*Gamma')*H' + R;% 新息序列方差阵
zNew = 15;
% 量测噪声方差自适应滤波处理
for t = 2:T
% 时间更新
xFault_pre = Phi*xFault(:,t-1); % 状态一步预测
P_pre = Phi*P0*Phi' + Gamma*Q*Gamma'; % 协方差一步预测的中间步骤
% 量测更新
beta(t) = beta(t-1)/(beta(t-1)+b); % 更新新息序列方差阵的系数
C = (1-beta(t))*C + beta(t)*(zNew*zNew');
if abs(trace(C)/trace(H*P_pre*H'+R_1s)) > 2 % 量测故障检测与隔离
xFault(:,t) = xFault_pre; % 无需量测更新,估计值用时间更新值代替
P0 = P_pre;
else
alpha = trace(C-H*P_pre*H')/trace(R_1s);
K = P_pre*H'*pinv(H*P_pre*H'+alpha*R_1s);
zNew = zMea(:,t)-H*xFault_pre;
xFault(:,t) = xFault_pre+ K*zNew;
P0 = (eye(2)-K*H)*P_pre;
end
end
% 画图
filerPlot(xState, zMea, xKF, 0, 0, 0, xFault, T, mode)
end
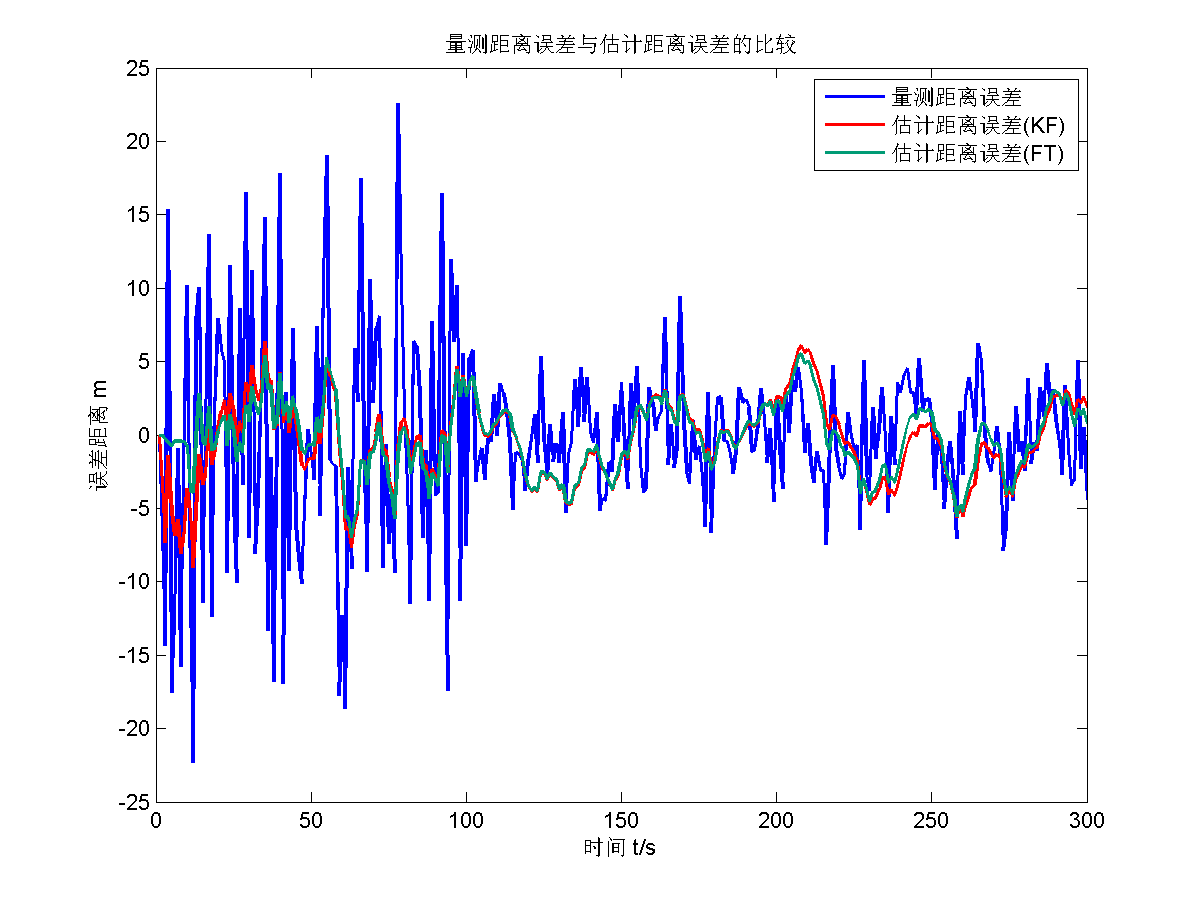
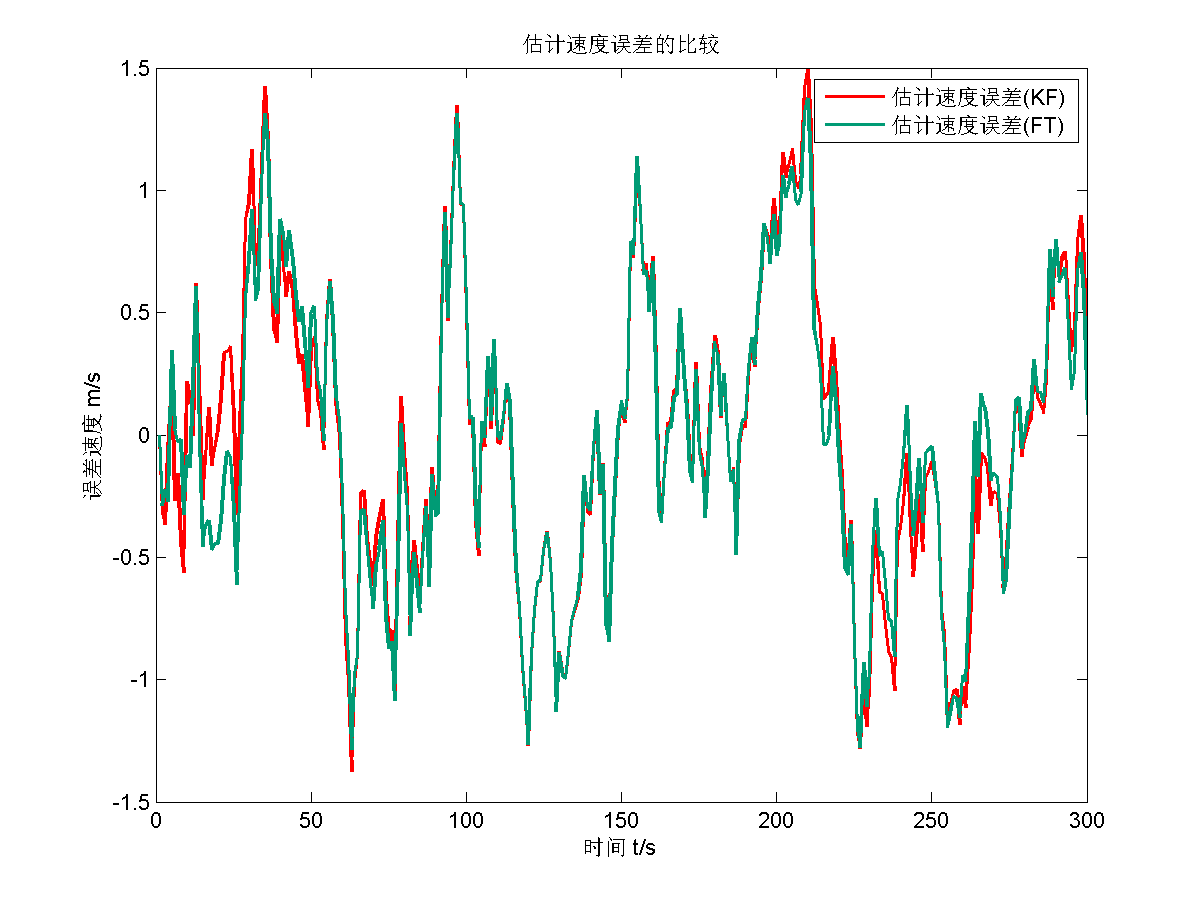
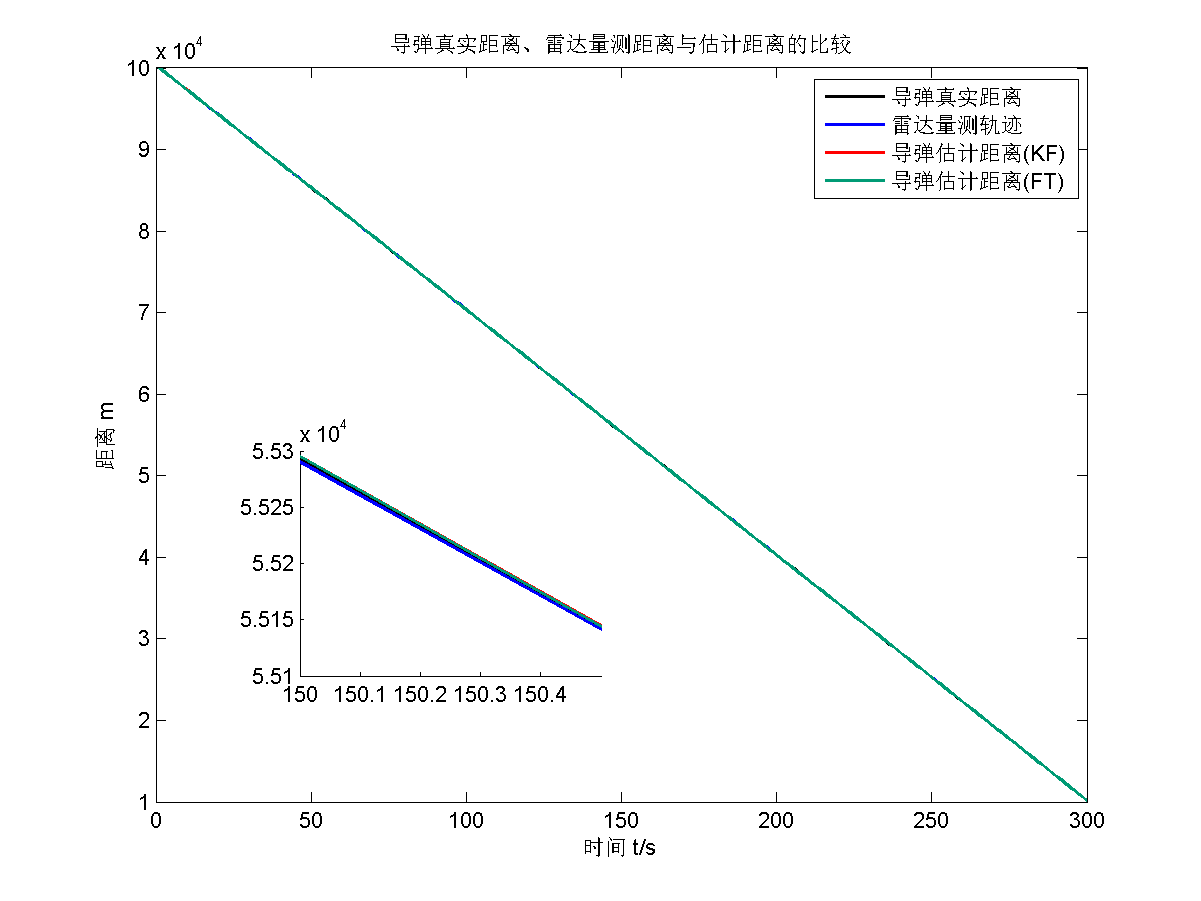
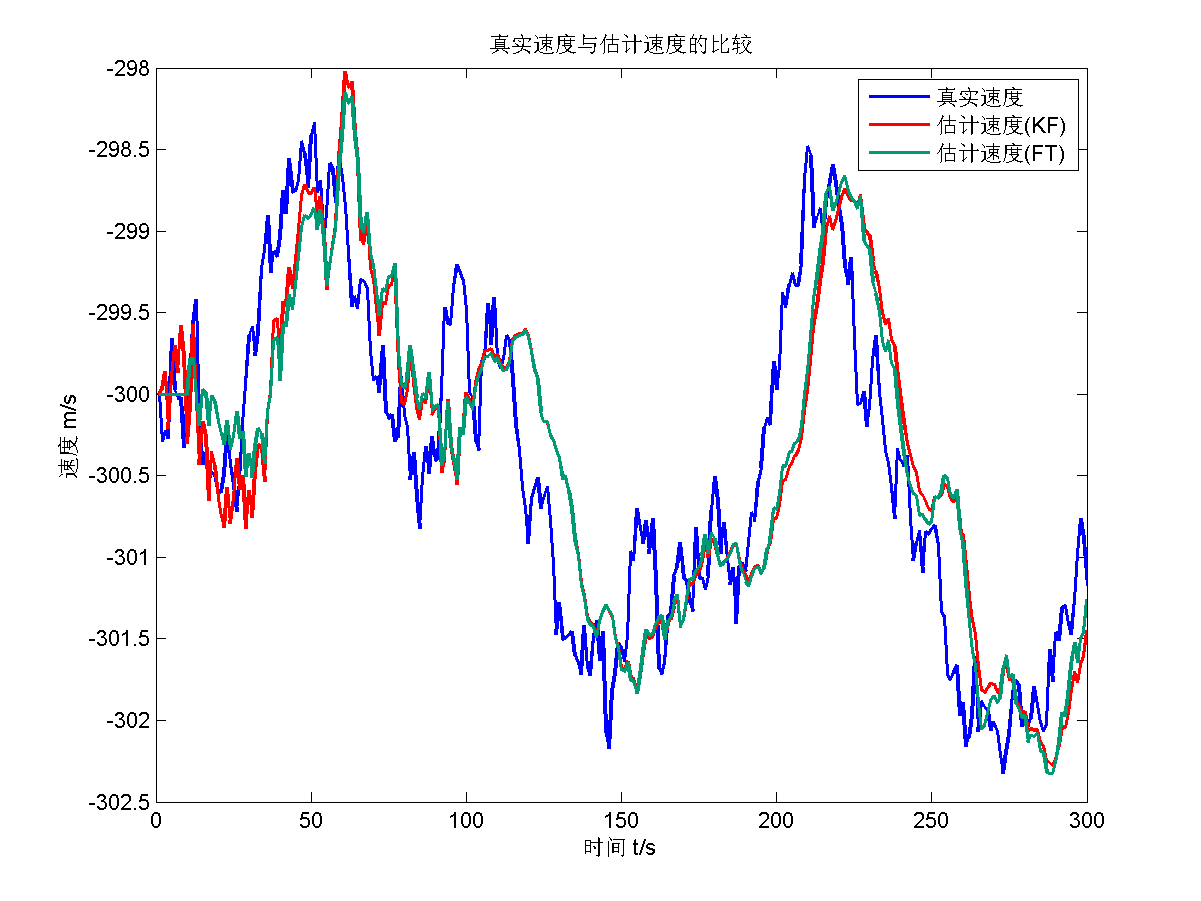
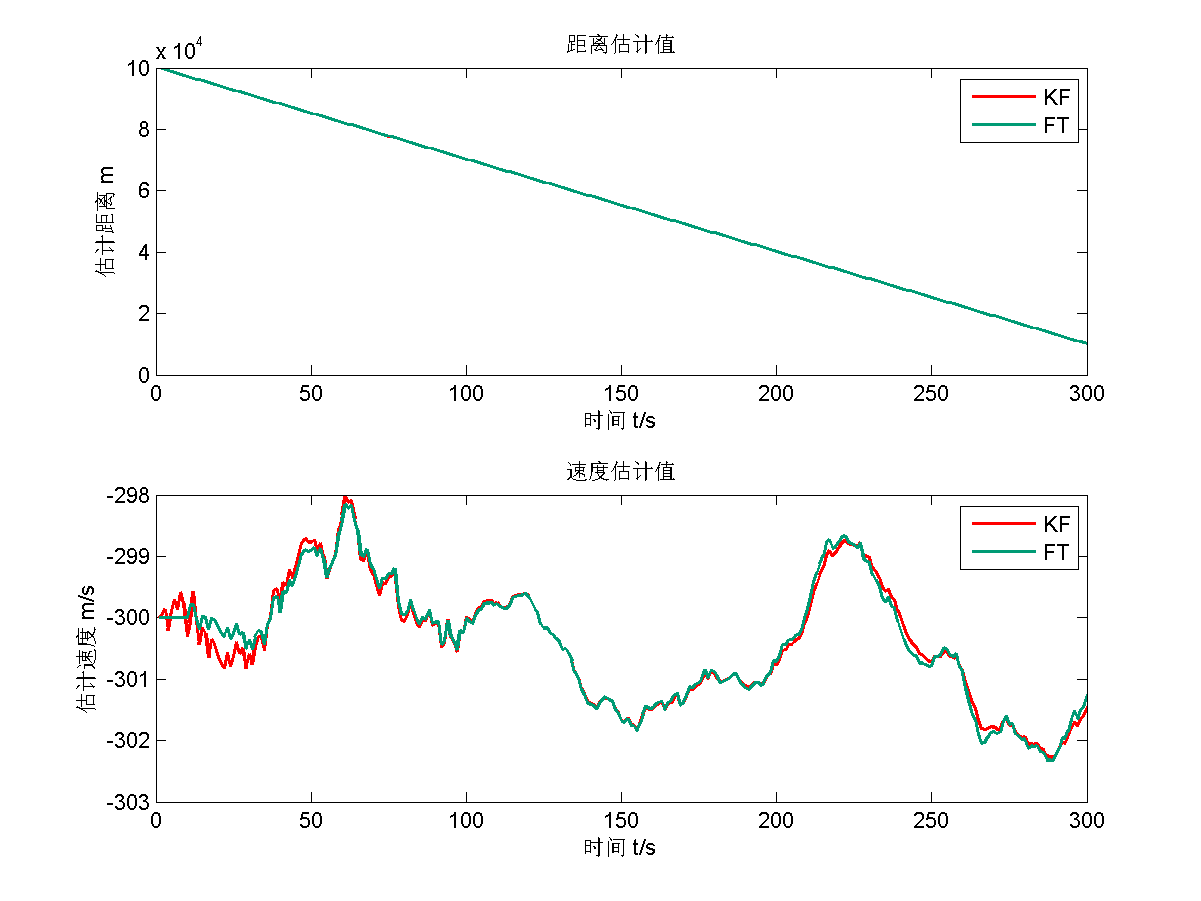
仿真结果为
Matlab仿真代码
在这里给出全部的Matlab仿真代码。
主函数main.m
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 功能描述:导弹运动Kalman滤波程序
% 课次:卡尔曼滤波与组合导航 第三次课程
% 时间:2021/5/12
% 作者:Lie Lie
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear;clc;close all;
%% 01 初始化参数
% 模式选择,选择要做仿真验证的习题
% mode = 'Problem 1'; % 习题1
% mode = 'Problem 2'; % 习题2
% mode = 'Problem 3'; % 习题3
% mode = 'Problem 4-1'; % 习题4-1
mode = 'Problem 4-2'; % 习题4-2
T = 300; % 仿真时长
Ts = 1; % 时间更新间隔
Q = 0.05*Ts; % 过程噪声
R = 50^2; % 量测噪声
W = sqrt(Q)*randn(1,T);
V = sqrt(R)*randn(1,T);
P0 = diag([10^2,1^2]); % 初始协方差阵
I0 = zeros(2,2); % 按照题目要求,初始信息阵设置为0
% 系统矩阵
A = [0 1;0 0]; % 状态矩阵
I = eye(2); % 单位阵
Phi = I + A*Ts; % 离散化
H = [1,0]; % 量测矩阵
Gamma = [0;1];
% 设置滤波维度
nS = 2; % 状态维度
nZ = 1; % 观测维度
% 分配空间
xState = zeros(nS,T); % 系统真实值
zMea = zeros(nZ,T); % 系统观测值
xKF = zeros(nS,T); % 卡尔曼滤波状态值
% 赋初值
xState(:,1) = [100000;-300]; % 系统状态初值
zMea(:,1) = H*xState(:,1); % 系统观测初值
xKF(:,1) = xState(:,1); % 卡尔曼滤波器估计初值
%% 02 用模型模拟真实状态
for t = 2:T
xState(:,t) = Phi*xState(:,t-1) + Gamma*W(:,t);
zMea(:,t) = H*xState(:,t) + V(t);
end
%% 03-1 Kalman滤波
% 针对习题3和4,不在此处做KF,节约计算资源
if ~strcmp(mode, 'Problem 3') && ~strcmp(mode, 'Problem 4-1') && ~strcmp(mode, 'Problem 4-2')
for t = 2:T
% 时间更新
xKF_pre = Phi*xKF(:,t-1);
P_pre = Phi*P0*Phi' + Gamma*Q*Gamma';
% 量测更新
K = P_pre*H'*pinv(H*P_pre*H'+R);
xKF(:,t) = xKF_pre+ K*(zMea(:,t)-H*xKF_pre);
P0 = (eye(2)-K*H)*P_pre;
end
end
%% 04-1 习题1:信息滤波
if strcmp(mode, 'Problem 1')
% 分配空间并赋予滤波器变量初值
sIF = zeros(nS,T); % 信息滤波状态值
xIF = zeros(nS,T);
sIF(:,1) = I0*xState(:,1); % 信息滤波器赋估计初值
Phi_inv = pinv(Phi); % 先求逆,减少计算量
Q_inv = 1/Q;
R_inv = 1/R;
for t = 2:T
M_k_1 = Phi_inv' * I0 * Phi_inv;
N_k_1 = M_k_1 * Gamma * pinv(Gamma'*M_k_1*Gamma + Q_inv) * Gamma';
S_pre = (I - N_k_1)*Phi_inv'*sIF(:,t-1);
I_pre = (I - N_k_1)*M_k_1;
sIF(:,t) = S_pre + H'*R_inv*zMea(:,t);
I0 = I_pre + H'*R_inv*H;
xIF(:,t) = pinv(I0)*sIF(:,t);
end
% 画图
filerPlot(xState, zMea, xKF, xIF, 0, 0, 0, T, mode)
end
%% 04-2 习题2:UD滤波
if strcmp(mode, 'Problem 2')
% 分配空间并赋予滤波器变量初值
xUD = zeros(nS,T); % UD滤波状态值
xUD(:,1) = xState(:,1); % UD滤波器赋估计初值
%注意!!!这里一定要再给一次 P0,不然这里的初始 P0 就是 KF 结束后的值了。
P0 = diag([10^2,1^2]); % 初始协方差阵
for t = 2:T
% 时间更新
xUD_pre = Phi*xUD(:,t-1);
[U, D] = udu(P0); % 将协方差阵作UD分解
[U, D] = UD_update(U, D, Phi, Gamma, Q, H, R, 'T'); % 将U和D进行时间更新,“T”意为Time update
P_pre = U*diag(D)*U';
% 量测更新
K = P_pre*H'*pinv(H*P_pre*H'+R);
xUD(:,t) = xUD_pre+ K*(zMea(:,t)-H*xUD_pre);
[U, D] = udu(P_pre); % 将一步预测协方差阵作UD分解
[U, D] = UD_update(U, D, Phi, Gamma, Q, H, R, 'M'); % 将U和D进行时间更新,“M”意为Measurement update
P0 = U*diag(D)*U';
end
% 画图
filerPlot(xState, zMea, xKF, 0, xUD, 0, 0, T, mode)
end
%% 04-3 习题3:遗忘滤波
if strcmp(mode, 'Problem 3')
% 根据题设条件,设置初始化参数
a = 1; % 加速度(m/s^2),减速机动,因为速度为负,所以这里符号为正
acc = [0.5*Ts^2;Ts]*a; % 构造矩阵
t_100 = 100; % 时间(s),导弹在第100秒时,减速机动
t_200 = 200; % 时间(s),导弹在第200秒后,停止减速机动,进入匀速运动
% 根据题设条件,用模型模拟真实状态
% 因为假定测量雷达仍认为导弹是匀速飞行,并建成匀速模型
% 故此处仍使用在代码第02节生成的量测数据 zMea
for t = 2:T
if t < t_100 || t >= t_200
xState(:,t) = Phi*xState(:,t-1) + Gamma*W(:,t);
elseif t >= t_100 && t < t_200
xState(:,t) = Phi*xState(:,t-1) + acc + Gamma*W(:,t);
end
zMea(:,t) = H*xState(:,t) + V(t);
end
% 分配空间并赋予滤波器变量初值
s = 1.1; % 渐消因子
xKF = zeros(nS,T); % 卡尔曼滤波状态值
xKF(:,1) = xState(:,1); % 卡尔曼滤波器估计初值
xFD = zeros(nS,T); % 遗忘滤波状态值
xFD(:,1) = xState(:,1); % 遗忘滤波器赋估计初值
% 再做一次卡尔曼滤波,先前第03-1节的卡尔曼滤波作废,因为 xState 发生变化了
for t = 2:T
[xKF(:,t), P0] = KF(xKF, P0, zMea, Phi, Gamma, H, Q, R, I, t);
end
% 遗忘滤波
% 因为上一步进行了卡尔曼滤波,P0的值发生了变化,因此需重新赋值一次
P0 = diag([10^2,1^2]); % 初始协方差阵
for t = 2:T
% 时间更新
xFD_pre = Phi*xFD(:,t-1);
P_pre = Phi*s*P0*Phi' + Gamma*Q*Gamma';
% 量测更新
K = P_pre*H'*pinv(H*P_pre*H'+R);
xFD(:,t) = xFD_pre+ K*(zMea(:,t)-H*xFD_pre);
P0 = (eye(2)-K*H)*P_pre;
end
% 画图
filerPlot(xState, zMea, xKF, 0, 0, xFD, 0, T, mode)
end
%% 04-4-1 习题4(1)
if strcmp(mode, 'Problem 4-1')
R_1s = 100; % 量测噪声方差为100m^2
R_100s = 10000; % 量测噪声方差为10000m^2
% 构造量测噪声序列,此处单位是方差,故需开方
V(1:100) = sqrt(R_1s)*randn(1,100); % 1-100s,方差为100m^2
V(101:T) = sqrt(R_100s)*randn(1,(T-100)); % 100s之后,方差为10000m^2
% 根据题设条件,用模型模拟真实状态
for t = 2:T
if t == 150 % 在150s时出现量测故障导致雷达输出为0
zMea(:,t) = 0;
else
zMea(:,t) = H*xState(:,t) + V(t);
end
end
% 再做一次卡尔曼滤波,先前第03-1节的卡尔曼滤波作废,因为 zMea 发生变化了
for t = 2:T
% 时间更新
xKF_pre = Phi*xKF(:,t-1);
P_pre = Phi*P0*Phi' + Gamma*Q*Gamma';
% 量测更新
K = P_pre*H'*pinv(H*P_pre*H'+R_1s);
xKF(:,t) = xKF_pre+ K*(zMea(:,t)-H*xKF_pre);
P0 = (eye(2)-K*H)*P_pre;
end
% 分配空间并赋予滤波器变量初值
xFault = zeros(nS,T); % 自适应遗忘滤波状态值
xFault(:,1) = xState(:,1); % 自适应遗忘滤波器赋估计初值
beta = zeros(1,T); beta(1) = 1;
b = 0.999; % 渐消因子
C = H*(Phi*P0*Phi' + Gamma*Q*Gamma')*H' + R;% 新息序列方差阵
zNew = 15;
% 量测噪声方差自适应滤波处理
for t = 2:T
% 时间更新
xFault_pre = Phi*xFault(:,t-1); % 状态一步预测
P_pre = Phi*P0*Phi' + Gamma*Q*Gamma'; % 协方差一步预测的中间步骤
% 量测更新
beta(t) = beta(t-1)/(beta(t-1)+b); % 更新新息序列方差阵的系数
C = (1-beta(t))*C + beta(t)*(zNew*zNew');
if abs(trace(C)/trace(H*P_pre*H'+R_1s)) > 2 % 量测故障检测与隔离
xFault(:,t) = xFault_pre; % 无需量测更新,估计值用时间更新值代替
P0 = P_pre;
else
alpha = trace(C-H*P_pre*H')/trace(R_1s);
K = P_pre*H'*pinv(H*P_pre*H'+alpha*R_1s);
zNew = zMea(:,t)-H*xFault_pre;
xFault(:,t) = xFault_pre+ K*zNew;
P0 = (eye(2)-K*H)*P_pre;
end
end
% 画图
filerPlot(xState, zMea, xKF, 0, 0, 0, xFault, T, mode)
end
%% 04-4-2 习题4(2)
if strcmp(mode, 'Problem 4-2')
R_1s = 100; % 量测噪声方差为100m^2
R_100s = 10; % 量测噪声方差为10m^2
% 构造量测噪声序列,此处单位是方差,故需开方
V(1:100) = sqrt(R_1s)*randn(1,100); % 1-100s,方差为100m^2
V(101:T) = sqrt(R_100s)*randn(1,(T-100)); % 100s之后,方差为10m^2
% 根据题设条件,用模型模拟真实状态
for t = 2:T
zMea(:,t) = H*xState(:,t) + V(t);
end
% 再做一次卡尔曼滤波,先前第03-1节的卡尔曼滤波作废,因为 zMea 发生变化了
for t = 2:T
% 时间更新
xKF_pre = Phi*xKF(:,t-1);
P_pre = Phi*P0*Phi' + Gamma*Q*Gamma';
% 量测更新
% 这里不要改变KF的R阵值
K = P_pre*H'*pinv(H*P_pre*H'+R_1s);
xKF(:,t) = xKF_pre+ K*(zMea(:,t)-H*xKF_pre);
P0 = (eye(2)-K*H)*P_pre;
end
% 分配空间并赋予滤波器变量初值
xFault = zeros(nS,T); % 自适应遗忘滤波状态值
xFault(:,1) = xState(:,1); % 自适应遗忘滤波器赋估计初值
beta = zeros(1,T); beta(1) = 1;
b = 0.999; % 渐消因子
C = H*(Phi*P0*Phi' + Gamma*Q*Gamma')*H' + R;% 新息序列方差阵
zNew = 15;
% 量测噪声方差自适应滤波处理
for t = 2:T
% 时间更新
xFault_pre = Phi*xFault(:,t-1); % 状态一步预测
P_pre = Phi*P0*Phi' + Gamma*Q*Gamma'; % 协方差一步预测的中间步骤
% 量测更新
beta(t) = beta(t-1)/(beta(t-1)+b); % 更新新息序列方差阵的系数
C = (1-beta(t))*C + beta(t)*(zNew*zNew');
if abs(trace(C)/trace(H*P_pre*H'+R_1s)) > 2 % 量测故障检测与隔离
xFault(:,t) = xFault_pre; % 无需量测更新,估计值用时间更新值代替
P0 = P_pre;
else
alpha = trace(C-H*P_pre*H')/trace(R_1s);
K = P_pre*H'*pinv(H*P_pre*H'+alpha*R_1s);
zNew = zMea(:,t)-H*xFault_pre;
xFault(:,t) = xFault_pre+ K*zNew;
P0 = (eye(2)-K*H)*P_pre;
end
end
% 画图
filerPlot(xState, zMea, xKF, 0, 0, 0, xFault, T, mode)
end
画图子函数filterPlot.m
function filerPlot(xState, zMea, xKF, xIF, xUD, xFD, xFT, T, mode)
saveFlag = 1; % 是否需要保存图片的标志
tPlot = 1:T;
figure('position',[300 300 550 450],'Color',[0.8 0.8 0.8],...
'Name','01-量测距离误差与估计距离误差的比较','NumberTitle','off');hold on;box on;
plot(tPlot,xState(1,:)-zMea(1,:),'-b','LineWidth',1.5);hold on;
plot(tPlot,xState(1,:)-xKF(1,:),'-r','LineWidth',1.5);hold on;
if strcmp(mode, 'Problem 1')
plot(tPlot,xState(1,:)-xIF(1,:),'-g','LineWidth',1.5);hold on;
legend('量测距离误差','估计距离误差(KF)','估计距离误差(IF)');
axis([0 T -150 150])
end
if strcmp(mode, 'Problem 2')
plot(tPlot,xState(1,:)-xUD(1,:),'-c','LineWidth',1.5);hold on;
legend('量测距离误差','估计距离误差(KF)','估计距离误差(UD)');
end
if strcmp(mode, 'Problem 3')
plot(tPlot,xState(1,:)-xFD(1,:),'-m','LineWidth',1.5);hold on;
legend('量测距离误差','估计距离误差(KF)','估计距离误差(FD)');
end
if strcmp(mode, 'Problem 4-1') || strcmp(mode, 'Problem 4-2')
plot(tPlot,xState(1,:)-xFT(1,:),'color',[0,0.61,0.46],'LineWidth',1.5);hold on;
legend('量测距离误差','估计距离误差(KF)','估计距离误差(FT)');
end
xlabel('时间 t/s');ylabel('误差距离 m');
title('量测距离误差与估计距离误差的比较');
% 保存图片
if saveFlag
saveas(gcf,'01-量测距离误差与估计距离误差的比较.png');
end
figure('position',[850 300 550 450],'Color',[0.8 0.8 0.8],...
'Name','02-真实速度与估计速度的比较','NumberTitle','off');hold on;box on;
plot(tPlot,xState(2,:)-xKF(2,:),'-r','LineWidth',1.5);hold on;
if strcmp(mode, 'Problem 1')
plot(tPlot,xState(2,:)-xIF(2,:),'-g','LineWidth',1.5);hold on;
legend('估计速度误差(KF)','估计速度误差(IF)');
axis([0 T -10 10])
end
if strcmp(mode, 'Problem 2')
plot(tPlot,xState(2,:)-xUD(2,:),'-c','LineWidth',1.5);hold on;
legend('估计速度误差(KF)','估计速度误差(UD)');
end
if strcmp(mode, 'Problem 3')
plot(tPlot,xState(2,:)-xFD(2,:),'-m','LineWidth',1.5);hold on;
legend('估计速度误差(KF)','估计速度误差(FD)');
end
if strcmp(mode, 'Problem 4-1') || strcmp(mode, 'Problem 4-2')
plot(tPlot,xState(2,:)-xFT(2,:),'color',[0,0.61,0.46],'LineWidth',1.5);hold on;
legend('估计速度误差(KF)','估计速度误差(FT)');
end
xlabel('时间 t/s');ylabel('误差速度 m/s');
title('估计速度误差的比较');
% 保存图片
if saveFlag
saveas(gcf,'02-真实速度与估计速度的比较.png');
end
figure('position',[300 200 550 450],'Color',[0.8 0.8 0.8],...
'Name','03-导弹真实距离、雷达量测距离与估计距离','NumberTitle','off');hold on;box on;
plot(tPlot,xState(1,:),'-k','LineWidth',1.5);hold on;
plot(tPlot,zMea(1,:),'-b','LineWidth',1.5);hold on;
plot(tPlot,xKF(1,:),'-r','LineWidth',1.5);hold on;
if strcmp(mode, 'Problem 1')
plot(tPlot,xIF(1,:),'-g','LineWidth',1.5);hold on;
legend('导弹真实距离','雷达量测轨迹','导弹估计距离(KF)','导弹估计距离(IF)');
end
if strcmp(mode, 'Problem 2')
plot(tPlot,xUD(1,:),'-c','LineWidth',1.5);hold on;
legend('导弹真实距离','雷达量测轨迹','导弹估计距离(KF)','导弹估计距离(UD)');
end
if strcmp(mode, 'Problem 3')
plot(tPlot,xFD(1,:),'-m','LineWidth',1.5);hold on;
legend('导弹真实距离','雷达量测轨迹','导弹估计距离(KF)','导弹估计距离(FD)');
end
if strcmp(mode, 'Problem 4-1') || strcmp(mode, 'Problem 4-2')
plot(tPlot,xFT(1,:),'color',[0,0.61,0.46],'LineWidth',1.5);hold on;
legend('导弹真实距离','雷达量测轨迹','导弹估计距离(KF)','导弹估计距离(FT)');
end
xlabel('时间 t/s');ylabel('距离 m');
title('导弹真实距离、雷达量测距离与估计距离的比较');
% 再画一张小图
axes('position',[0.25,0.25,0.25,0.25]);hold on;
plot(tPlot,xState(1,:),'-k','LineWidth',1.5);hold on;
plot(tPlot,zMea(1,:),'-b','LineWidth',1.5);hold on;
plot(tPlot,xKF(1,:),'-r','LineWidth',1.5);hold on;
if strcmp(mode, 'Problem 1')
plot(tPlot,xIF(1,:),'-g','LineWidth',1.5);hold on;
end
if strcmp(mode, 'Problem 2')
plot(tPlot,xUD(1,:),'-c','LineWidth',1.5);hold on;
end
if strcmp(mode, 'Problem 3')
plot(tPlot,xFD(1,:),'-m','LineWidth',1.5);hold on;
end
if strcmp(mode, 'Problem 4-1') || strcmp(mode, 'Problem 4-2')
plot(tPlot,xFT(1,:),'color',[0,0.61,0.46],'LineWidth',1.5);hold on;
end
xlim([T/2,T/2+0.5]);
% 保存图片
if saveFlag
saveas(gcf,'03-导弹真实距离、雷达量测距离与估计距离.png');
end
figure('position',[850 200 550 450],'Color',[0.8 0.8 0.8],...
'Name','04-导弹真实速度与估计速度的比较','NumberTitle','off');hold on;box on;
plot(tPlot,xState(2,:),'-b','LineWidth',1.5);hold on;
plot(tPlot,xKF(2,:),'-r','LineWidth',1.5);hold on;
if strcmp(mode, 'Problem 1')
plot(tPlot,xIF(2,:),'-g','LineWidth',1.5);hold on;
legend('真实速度','估计速度(KF)','估计速度(IF)');
axis([0 T -310 -290])
end
if strcmp(mode, 'Problem 2')
plot(tPlot,xUD(2,:),'-c','LineWidth',1.5);hold on;
legend('真实速度','估计速度(KF)','估计速度(UD)');
end
if strcmp(mode, 'Problem 3')
plot(tPlot,xFD(2,:),'-m','LineWidth',1.5);hold on;
legend('真实速度','估计速度(KF)','估计速度(FD)',2);
end
if strcmp(mode, 'Problem 4-1') || strcmp(mode, 'Problem 4-2')
plot(tPlot,xFT(2,:),'color',[0,0.61,0.46],'LineWidth',1.5);hold on;
legend('真实速度','估计速度(KF)','估计速度(FT)');
end
xlabel('时间 t/s');ylabel('速度 m/s');
title('真实速度与估计速度的比较');
% 保存图片
if saveFlag
saveas(gcf,'04-真实速度与估计速度的比较.png');
end
figure('position',[300 100 550 450],'Color',[0.8 0.8 0.8],...
'Name','05-估计距离与估计速度','NumberTitle','off');hold on;box on;
subplot(211);
plot(tPlot,xKF(1,:),'-r','LineWidth',1.5);hold on;
if strcmp(mode, 'Problem 1')
plot(tPlot,xIF(1,:),'-g','LineWidth',1.5);hold on;
legend('KF','IF');
end
if strcmp(mode, 'Problem 2')
plot(tPlot,xUD(1,:),'-c','LineWidth',1.5);hold on;
legend('KF','UD');
end
if strcmp(mode, 'Problem 3')
plot(tPlot,xFD(1,:),'-m','LineWidth',1.5);hold on;
legend('KF','FD');
end
if strcmp(mode, 'Problem 4-1') || strcmp(mode, 'Problem 4-2')
plot(tPlot,xFT(1,:),'color',[0,0.61,0.46],'LineWidth',1.5);hold on;
legend('KF','FT');
end
xlabel('时间 t/s');ylabel('估计距离 m');
title('距离估计值');
subplot(212);
plot(tPlot,xKF(2,:),'-r','LineWidth',1.5);hold on;
if strcmp(mode, 'Problem 1')
plot(tPlot,xIF(2,:),'-g','LineWidth',1.5);hold on;
legend('KF','IF');
axis([0 T -310 -290])
end
if strcmp(mode, 'Problem 2')
plot(tPlot,xUD(2,:),'-c','LineWidth',1.5);hold on;
legend('KF','UD');
end
if strcmp(mode, 'Problem 3')
plot(tPlot,xFD(2,:),'-m','LineWidth',1.5);hold on;
legend('KF','FD');
end
if strcmp(mode, 'Problem 4-1') || strcmp(mode, 'Problem 4-2')
plot(tPlot,xFT(2,:),'color',[0,0.61,0.46],'LineWidth',1.5);hold on;
legend('KF','FT');
end
xlabel('时间 t/s');ylabel('估计速度 m/s');
title('速度估计值');
% 保存图片
if saveFlag
saveas(gcf,'05-估计距离与估计速度.png');
end
end