用卡尔曼滤波器跟踪导弹（量测更新频率与时间更新频率不相等）

2021-05-12

题目

巡航导弹沿直线飞向目标，目标处设有一监视雷达，雷达对导弹的距离进行观测。假设：（1）导弹初始距离$100km$，速度约为$300m/s$，基本匀速飞行，但受空气扰动影响，扰动加速度为零均值白噪声，方差强度$q=0.05m^2/s^3$ ；（2）雷达观测频率$2Hz$，观测误差为零均值白噪声，均方差为$50m$；（3）时间更新频率10Hz。对比该结果与时间/量测更新频率均为2Hz的差别。试使用卡尔曼滤波（Kalman filter）完成导弹的轨迹跟踪。

【解】时间更新频率为10HZ，量测更新频率为2HZ，即时间更新5次，状态更新1次。

代码如下：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 功能描述：导弹运动Kalman滤波程序
% 课次：卡尔曼滤波与组合导航 第二次课程
% 时间：2021/5/4
% 作者：Lei Lie
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear;clc;close all;
%% 01 初始化参数
T = 300;                   % 仿真时长

T_mea = 1/2;               % 量测采样时间
T_update = 1/10;           % 时间更新间隔
Q = 0.05*T_update;         % 过程噪声 
R = 50;                    % 量测噪声
W = sqrt(Q)*randn(1,T);
V = sqrt(R)*randn(1,T);
P0 = diag([10^2,1^2]);  

% 系统矩阵
A = [0 -1;0 0];            % 状态矩阵
I = eye(2);
Phi = I + A*T_update;      % 离散化 
H = [1,0];                 % 量测矩阵
Gamma = [0;1];

% 初始化
nS = 2; nZ = 1;
count = 1;                % 用于计数
xState = zeros(nS,T);
zMea = zeros(nZ,T);
xKF_10HZ = zeros(nS,T);
xKF_2HZ = zeros(nS,T);
xKF_pre = zeros(nS,T);
xState(:,1) = [100000;300];
zMea(:,1) = H*xState(:,1);
xKF_10HZ(:,1) = xState(:,1);
xKF_2HZ(:,1) = xState(:,1);
%% 02 用模型模拟真实状态
for t = 2:T
    xState(:,t) = Phi*xState(:,t-1) + Gamma*W(:,t);
    zMea(:,t) = H*xState(:,t) + V(t);
end
%% 03-1 Kalman滤波（时间更新为10Hz,量测频率为2Hz）
for t = 2:T
    % 时间更新（时间更新为10Hz）
    xKF_pre(:,t) = Phi*xKF_10HZ(:,t-1);
    P_pre = Phi*P0*Phi' + Gamma*Q*Gamma';
    % 量测更新（量测频率为2Hz）
    if (mod(count,T_mea/T_update)==0)       % 时间更新5次，量测1次
        K = P_pre*H'*pinv(H*P_pre*H'+R);
        xKF_10HZ(:,t) = xKF_pre(:,t) + K*(zMea(:,t)-H*xKF_pre(:,t));
        P0 = (I-K*H)*P_pre;
        count = 1;                          % 计数归0
    else
        xKF_10HZ(:,t) = xKF_pre(:,t);       % 将上一拍的值传给滤波器
        P0 = P_pre;
        count = count + 1;                  % 计数加1
    end
end

%% 03-2 Kalman滤波（时间更新为2Hz,量测频率为2Hz）
for t = 2:T
    % 时间更新（时间更新为2Hz）
    xKF_pre(:,t) = Phi*xKF_2HZ(:,t-1);
    P_pre = Phi*P0*Phi' + Gamma*Q*Gamma';
    % 量测更新（量测频率为2Hz）
    K = P_pre*H'*pinv(H*P_pre*H'+R);
    xKF_2HZ(:,t) = xKF_pre(:,t) + K*(zMea(:,t)-H*xKF_pre(:,t));
    P0 = (I-K*H)*P_pre;
end

%% 04 画图
tPlot = 1:T;
FigWin1=figure('position',[300 300 550 450],'Color',[0.8 0.8 0.8],...
   'Name','01-量测距离误差与估计距离误差的比较','NumberTitle','off');hold on;box on;
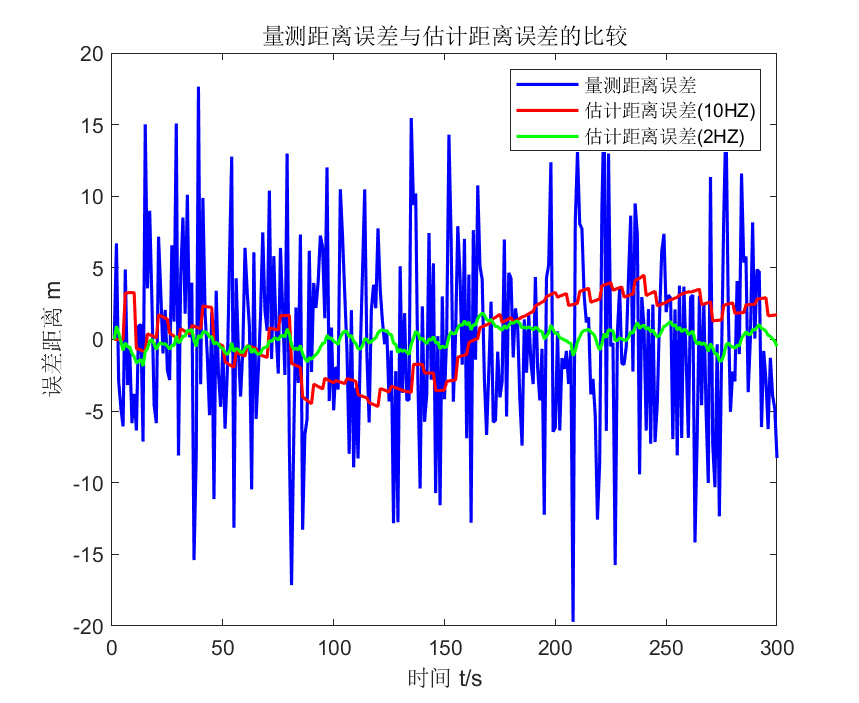
plot(tPlot,xState(1,:)-zMea(1,:),'-b','LineWidth',1.5);hold on;
plot(tPlot,xState(1,:)-xKF_10HZ(1,:),'-r','LineWidth',1.5);hold on;
plot(tPlot,xState(1,:)-xKF_2HZ(1,:),'-g','LineWidth',1.5);hold on;
xlabel('时间 t/s');ylabel('误差距离 m');
legend('量测距离误差','估计距离误差(10HZ)','估计距离误差(2HZ)');
title('量测距离误差与估计距离误差的比较');
% 保存图片
saveas(gcf,'01-量测距离误差与估计距离误差的比较.png');

FigWin2=figure('position',[850 300 550 450],'Color',[0.8 0.8 0.8],...
   'Name','02-真实速度与估计速度的比较','NumberTitle','off');hold on;box on;
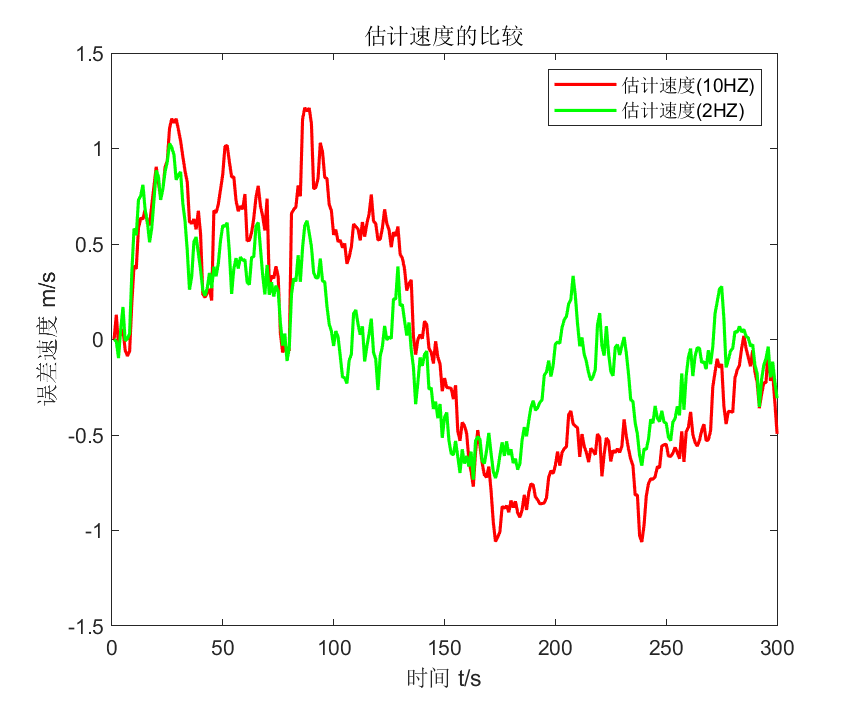
plot(tPlot,xState(2,:)-xKF_10HZ(2,:),'-r','LineWidth',1.5);hold on;
plot(tPlot,xState(2,:)-xKF_2HZ(2,:),'-g','LineWidth',1.5);hold on;
xlabel('时间 t/s');ylabel('误差速度 m/s');
legend('估计速度(10HZ)','估计速度(2HZ)');
title('估计速度的比较');
% 保存图片
saveas(gcf,'02-真实速度与估计速度的比较.png');

FigWin3=figure('position',[300 200 550 450],'Color',[0.8 0.8 0.8],...
   'Name','03-导弹真实距离、雷达量测距离与估计距离','NumberTitle','off');hold on;box on;
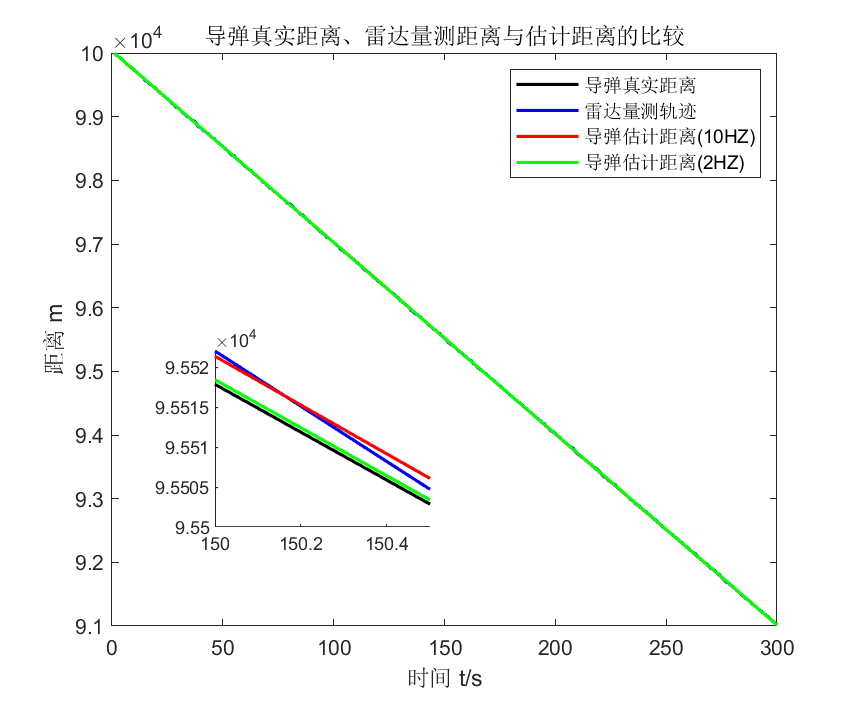
plot(tPlot,xState(1,:),'-k','LineWidth',1.5);hold on;
plot(tPlot,zMea(1,:),'-b','LineWidth',1.5);hold on;
plot(tPlot,xKF_10HZ(1,:),'-r','LineWidth',1.5);hold on;
plot(tPlot,xKF_2HZ(1,:),'-g','LineWidth',1.5);hold on;
xlabel('时间 t/s');ylabel('距离 m');
legend('导弹真实距离','雷达量测轨迹','导弹估计距离(10HZ)','导弹估计距离(2HZ)');
title('导弹真实距离、雷达量测距离与估计距离的比较');
axes('position',[0.25,0.25,0.25,0.25]);
hold on;
plot(tPlot,xState(1,:),'-k','LineWidth',1.5);hold on;
plot(tPlot,zMea(1,:),'-b','LineWidth',1.5);hold on;
plot(tPlot,xKF_10HZ(1,:),'-r','LineWidth',1.5);hold on;
plot(tPlot,xKF_2HZ(1,:),'-g','LineWidth',1.5);hold on;
xlim([T/2,T/2+0.5]);
% 保存图片
saveas(gcf,'03-导弹真实距离、雷达量测距离与估计距离.png');

FigWin4=figure('position',[850 200 550 450],'Color',[0.8 0.8 0.8],...
   'Name','04-导弹真实速度与估计速度的比较','NumberTitle','off');hold on;box on;
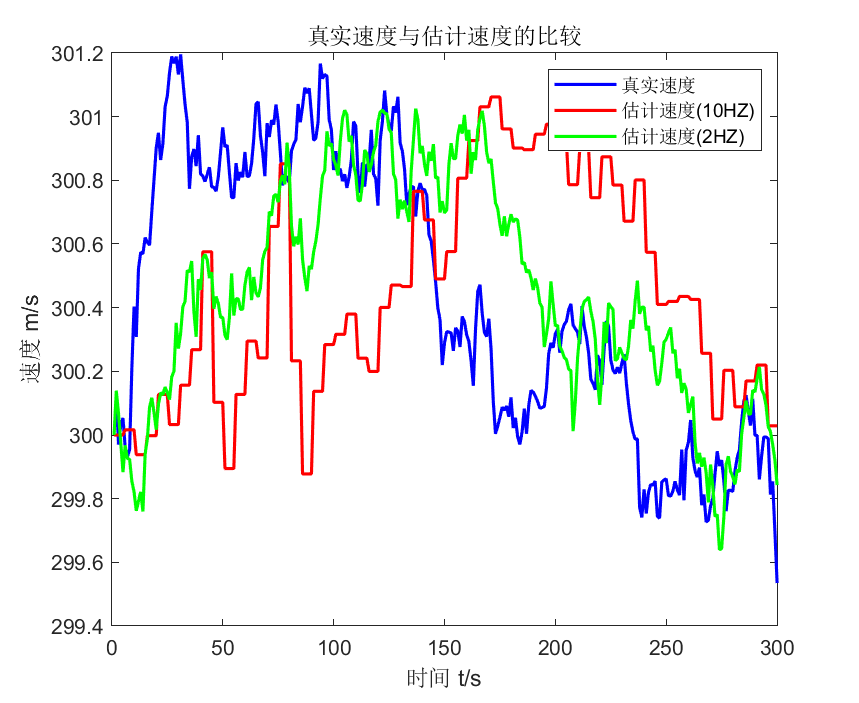
plot(tPlot,xState(2,:),'-b','LineWidth',1.5);hold on;
plot(tPlot,xKF_10HZ(2,:),'-r','LineWidth',1.5);hold on;
plot(tPlot,xKF_2HZ(2,:),'-g','LineWidth',1.5);hold on;
xlabel('时间 t/s');ylabel('速度 m/s');
legend('真实速度','估计速度(10HZ)','估计速度(2HZ)');
title('真实速度与估计速度的比较');
% 保存图片
saveas(gcf,'04-真实速度与估计速度的比较.png');

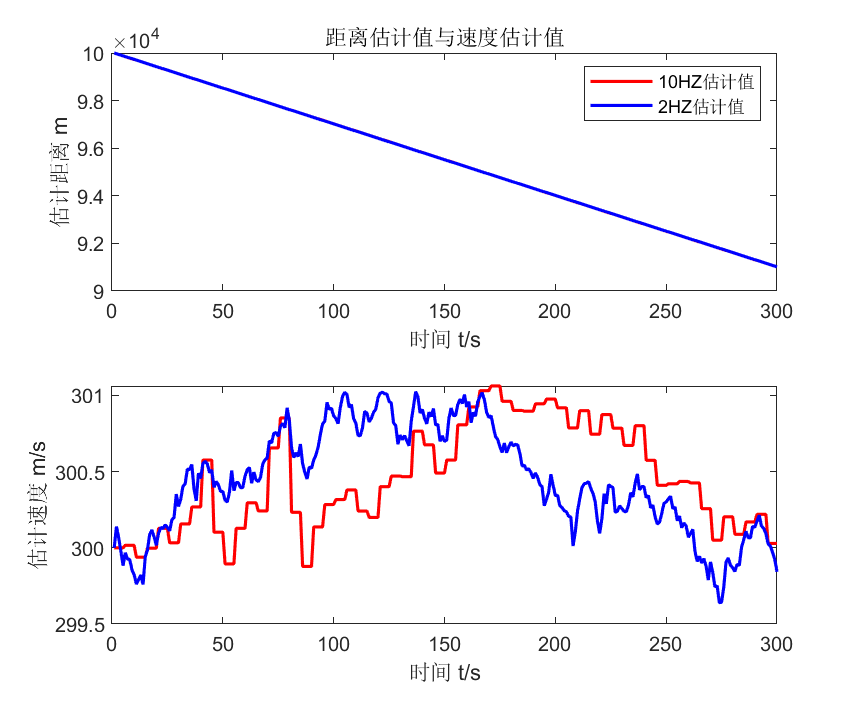
FigWin5=figure('position',[300 100 550 450],'Color',[0.8 0.8 0.8],...
   'Name','05-估计距离与估计速度','NumberTitle','off');hold on;box on;
subplot(211);
plot(tPlot,xKF_10HZ(1,:),'-r','LineWidth',1.5);hold on;
plot(tPlot,xKF_2HZ(1,:),'-b','LineWidth',1.5);hold on;
legend('10HZ估计值','2HZ估计值');
xlabel('时间 t/s');ylabel('估计距离 m');
title('距离估计值与速度估计值');
subplot(212);
plot(tPlot,xKF_10HZ(2,:),'-r','LineWidth',1.5);hold on;
plot(tPlot,xKF_2HZ(2,:),'-b','LineWidth',1.5);hold on;
xlabel('时间 t/s');ylabel('估计速度 m/s');
% 保存图片
saveas(gcf,'05-估计距离与估计速度.png');

仿真结果图如下所示。

01-量测距离误差与估计距离误差的比较

02-真实速度与估计速度的比较

03-导弹真实距离、雷达量测距离与估计距离

04-真实速度与估计速度的比较

05-估计距离与估计速度

雷烈

题目