Lanchester方程的离散模型及Python代码实现

2021-05-11

利用差分的方法将连续域的Lanchester方程离散化，以得到战争双方的兵力损耗情况。

下面对间瞄火力的Lanchester方程、平方律的Lanchester方程和考虑了信息对抗因素的Lanchester方程进行离散化，并给出了对应的离散方程。

（1）间瞄火力的Lanchester方程

公式

离散化后的公式如下：

\[\left\{\begin{matrix} R(k+1) = R(k) - a_lB(k)R(k) \\ B(k+1) = B(k) - b_lB(k)R(k) \end{matrix}\right. \tag{1}\]

参数说明

$R(k)$、$B(k)$ 分别表示红、蓝双方在 $k$ 的兵力情况，此处取初值为 $R_0=8000$、$B_0=10000$ ；
$b_l$ 、$a_l$分别表示红、蓝双方战斗单位的作战效能，此处取 $b_l=0.00001$ 、$a_l=0.00002$。（一定要注意这里！$b_l$ 、$a_l$ 的位置是反的！不是按照顺序给了红、蓝双方，这篇论文在引言和第1.2节中的定义有冲突，为写公式不出错，我采用了作者第1.2节的写法。）

Python 代码实现

定义了一个LinearLaw()函数来实现间瞄火力的Lanchester方程，代码如下。

def LinearLaw(R, B, b_l, a_l, t):
    R.append(R[t] - a_l * B[t] * R[t])
    B.append(B[t] - b_l * B[t] * R[t])
    return R, B

这里有个判断哪一方交战胜利的等式，如果红、蓝双方兵力满足下面等式 $R_0b_l>B_0a_l$ 则说明红方必将获胜。代码如下

elif mode == "LinearLaw":                   # 根据间瞄火力的胜负条件做比较
    if R0 * b > B0 * a:
        print("红方将【取得胜利】！")
    else:
        print("蓝方将【取得胜利】！")

仿真结果如下图所示，源代码将在文章的末尾给出。

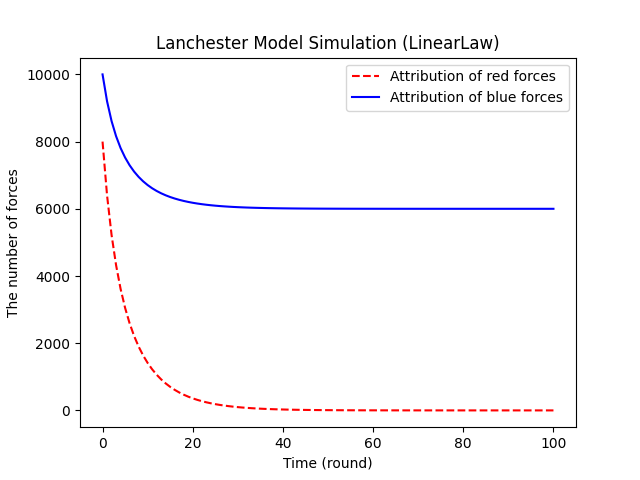
LinearLaw

（2）平方律的Lanchester方程

公式

离散化后的公式如下：

\[\left\{\begin{matrix} R(k+1) = R(t) - a_sB(t) \\ B(k+1) = B(k) - b_sR(t) \end{matrix}\right. \tag{2}\]

参数说明

$R(k)$、$B(k)$ 分别表示红、蓝双方在 $k$ 的兵力情况，此处取初值为 $R_0=8000$、$B_0=10000$ ；
$b_s$ 、$a_s$分别表示红、蓝双方战斗单位在单位时间内平均毁伤对方战斗成员的数量，此处取 $b_s=0.1$ 、$a_s=0.2$。（一定要注意这里！$b_s$ 、$a_s$ 的位置是反的！不是按照顺序给了红、蓝双方，这篇论文在引言和第1.2节中的定义有冲突，为写公式不出错，我采用了作者第1.2节的写法。）

Python 代码实现

定义了一个SquareLaw()函数来实现平方律的Lanchester方程，代码如下。

def SquareLaw(R, B, b_s, a_s, t):
    R.append(R[t] - a_s * B[t])
    B.append(B[t] - b_s * R[t])
    return R, B

这里有个判断哪一方交战胜利的等式，如果红、蓝双方兵力满足下面等式

\[R_0^2b_l>B_0^2a_l\]

则说明红方必将获胜。代码如下

R0_square = R0 ** 2                     # 红方兵力的平方
B0_square = B0 ** 2                     # 蓝方兵力的平方
if R0_square * b > B0_square * a:       # 根据平方律的胜负条件做比较
    print("红方将【取得胜利】！")
else:
    print("蓝方将【取得胜利】！")

仿真结果如下图所示，源代码将在文章的末尾给出。

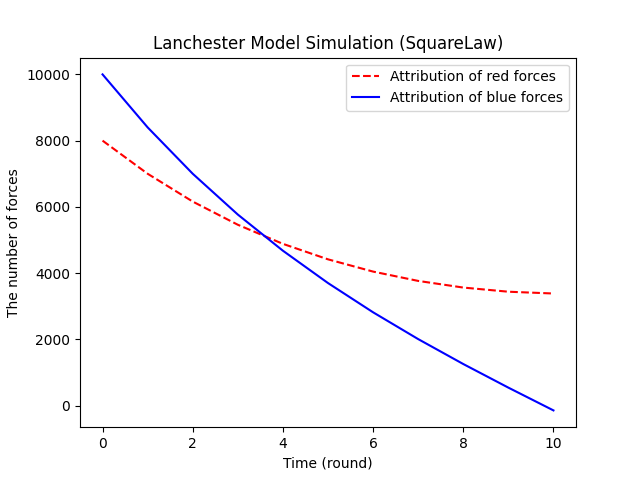
SquareLaw

（3）信息对抗因素的Lanchester方程

公式

离散化后的公式如下：

\[\left\{\begin{matrix} R(k+1) = R(t) - (1-f_r)s_bb_sB(k)\varepsilon_b - (1-(1-f_r)s_b)b_lB(k)R(k)\varepsilon_b\\ B(k+1) = B(k) - (1-f_b)s_ra_sR(k)\varepsilon_r - (1-(1-f_b)s_r)a_lB(k)R(k)\varepsilon_r \end{matrix}\right. \tag{3}\]

注意：这篇论文给出的公式是错的，在计算 $B(k+1)$ 时，下面的等式最后一项括号里面的符号应为$(1-(1-\boldsymbol{f_b})s_r)$，而非原文中的$(1-(1-\boldsymbol{f_r})s_r)$。

参数说明

$R(k)$、$B(k)$ 分别表示红、蓝双方在 $k$ 的兵力情况，此处取初值为 $R_0=8000$、$B_0=10000$ ；
$b_l$ 、$a_l$分别表示红、蓝双方战斗单位的作战效能，此处取 $b_l=0.00001$ 、$a_l=0.00002$；
$b_s$ 、$a_s$分别表示红、蓝双方战斗单位在单位时间内平均毁伤对方战斗成员的数量，此处取 $b_s=0.1$ 、$a_s=0.2$；
$f_r$、$f_b$ 为红、蓝双方的伪装能力系数，此处取 $f_r=0.6$、$f_b=0.2$；
$s_r$、$s_b$ 为红、蓝双方的侦察能力，此处取 $s_r=0.6$、$s_b=0.2$ ；
$\varepsilon_r$、$\varepsilon_b$ 为红、蓝双方的信息作战能力系数，此处取 $\varepsilon_r=4$、$\varepsilon_b=4$ 。

Python 代码实现

定义了一个MoLanMdl()函数来实现间瞄火力的Lanchester方程，代码如下。

def MoLanMdl(R, B, b_s, a_s, b_l, a_l, f_r, s_r, f_b, s_b, e_r, e_b, t):
    rValue = R[t] - (1-f_r)*s_b*b_s*B[t]*e_b - (1-(1-f_r)*s_b)*b_l*B[t]*R[t]*e_b
    bValue = B[t] - (1-f_b)*s_r*a_s*R[t]*e_r - (1-(1-f_b)*s_r)*a_l*B[t]*R[t]*e_r
    R.append(rValue)
    B.append(bValue)
    return R, B

这里没给双方交战胜利的判断条件。

仿真结果如下图所示，源代码将在文章的末尾给出。

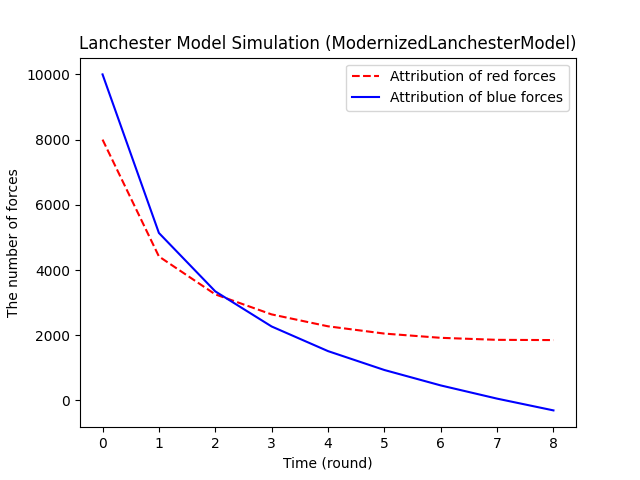
ModernizedLanchesterModel

Python 代码

源码如下

# encoding: utf-8
"""
#-------------------------------------------------------------------#
#                      Lei Lie's Python Code                        #     
#-------------------------------------------------------------------#
#                   @Project Name : Python代码                      #
#                   @File Name    : mainZhanDonghui.py              #
#                   @Programmer   : Lei Lie                         #
#                   @Start Date   : 2021/5/11                       #
#                   @Last Update  : 2021/5/11                       #
#-------------------------------------------------------------------#
# Function:                                                         #
#         论文《现代化战争条件下的兰切斯特战斗模型》的代码复现        #
#-------------------------------------------------------------------#
"""
import numpy as np
import matplotlib.pyplot as plt


def predict(R0, B0, b, a, mode):
    print("——————————————————————————————————————————————")
    print("战斗过程预测结果为：")
    if mode == "SquareLaw":
        R0_square = R0 ** 2                     # 红方兵力的平方
        B0_square = B0 ** 2                     # 蓝方兵力的平方
        if R0_square * b > B0_square * a:       # 根据平方律的胜负条件做比较
            print("红方将【取得胜利】！")
        else:
            print("蓝方将【取得胜利】！")
    elif mode == "LinearLaw":
        if R0 * b > B0 * a:
            print("红方将【取得胜利】！")
        else:
            print("蓝方将【取得胜利】！")


def finalTroops(r, b):
    print("红方剩余兵力为【", r, "】")
    print("蓝方剩余兵力为【", b, "】")


def SquareLaw(R, B, b_s, a_s, t):
    R.append(R[t] - a_s * B[t])
    B.append(B[t] - b_s * R[t])
    return R, B


def LinearLaw(R, B, b_l, a_l, t):
    R.append(R[t] - a_l * B[t] * R[t])
    B.append(B[t] - b_l * B[t] * R[t])
    return R, B


def MoLanMdl(R, B, b_s, a_s, b_l, a_l, f_r, s_r, f_b, s_b, e_r, e_b, t):
    rValue = R[t] - (1-f_r)*s_b*b_s*B[t]*e_b - (1-(1-f_r)*s_b)*b_l*B[t]*R[t]*e_b
    bValue = B[t] - (1-f_b)*s_r*a_s*R[t]*e_r - (1-(1-f_b)*s_r)*a_l*B[t]*R[t]*e_r
    R.append(rValue)
    B.append(bValue)
    return R, B


if __name__ == '__main__':
    # 初始参数
    R0 = 8000                                   # 红方兵力
    B0 = 10000                                  # 蓝方兵力
    b_l = 0.00001                               # 红方战斗单位作战效能
    a_l = 0.00002                               # 蓝方战斗单位作战效能
    b_s = 0.2                                   # 红方战斗单位在单位时间平均毁伤对方战斗成员的数量
    a_s = 0.1                                   # 蓝方战斗单位在单位时间平均毁伤对方战斗成员的数量

    R = [R0, ]                                  # 用于记录红方兵力变化的列表
    B = [B0, ]                                  # 用于记录蓝方病理变化的列表

    T = 100                                     # 仿真总步长
    dt = 1                                      # 时间间隔

    # mode = "SquareLaw"
    # mode = "LinearLaw"
    mode = "ModernizedLanchesterModel"

    if mode == "SquareLaw":                     # 采用平方律的战斗过程
        # 预测战斗进程
        predict(R0, B0, b_s, a_s, mode)
        for t in np.arange(0, T, dt):
            SquareLaw(R, B, b_s, a_s, t)
            if R[-1] < 1e-6 or B[-1] < 1e-6:
                break
    elif mode == "LinearLaw":                   # 采用线性律的战斗过程
        predict(R0, B0, b_l, a_l, mode)
        for t in np.arange(0, T, dt):
            LinearLaw(R, B, b_l, a_l, t)
            if R[-1] < 1e-6 or B[-1] < 1e-6:
                break
    elif mode == "ModernizedLanchesterModel":
        # 初始化参数
        f_r = 0.6                               # 红方的伪装能力系数
        s_r = 0.6                               # 红方的侦察能力
        f_b = 0.2                               # 蓝方的伪装能力系数
        s_b = 0.2                               # 蓝方的侦察能力
        epsilon_r = 4                           # 红方信息作战能力系数
        epsilon_b = 4                           # 蓝方信息作战能力系数
        for t in np.arange(0, T, dt):
            MoLanMdl(R, B, b_s, a_s, b_l, a_l, f_r, s_r, f_b, s_b, epsilon_r, epsilon_b, t)
            if R[-1] < 1e-6 or B[-1] < 1e-6:
                break
        print("——————————————————————————————————————————————")
        print("战斗过程预测结果为：")
        if R[-1] > B[-1]:
            print("红方将【取得胜利】！")
        else:
            print("蓝方将【取得胜利】！")
    print("——————————————————————————————————————————————")
    finalTroops(R[-1], B[-1])                   # 打印红、蓝双方最终剩余兵力
    print("——————————————————————————————————————————————")

    '''画图'''
    tPlot = np.arange(0, len(R) * dt, dt)
    plt.figure(1)
    plt.plot(tPlot, R, '--r', label='Attribution of red forces')
    plt.plot(tPlot, B, 'b', label='Attribution of blue forces')
    plt.xlabel("Time (round)")
    plt.ylabel("The number of forces")
    # plt.xlim(0, len(R) * dt)
    # plt.ylim(0, B0 + 0.5)
    plt.title("Lanchester Model Simulation"+" ("+mode+")")
    plt.legend()
    plt.show()

代码解释

（1）模式选择

# mode = "SquareLaw"
# mode = "LinearLaw"
mode = "ModernizedLanchesterModel"

这三行代码用来选择要仿真的模式。

mode = "SquareLaw"

即仿真验证平方律的Lanchester方程。

mode = "LinearLaw"

即仿真验证间瞄火力的Lanchester方程。

mode = "ModernizedLanchesterModel"

即仿真验证现代战争模式下的Lanchester方程

（2）进行仿真

if mode == "SquareLaw":                     # 采用平方律的战斗过程
    # 预测战斗进程
    predict(R0, B0, b_s, a_s, mode)
    for t in np.arange(0, T, dt):
        SquareLaw(R, B, b_s, a_s, t)
        if R[-1] < 1e-6 or B[-1] < 1e-6:
            break
elif mode == "LinearLaw":                   # 采用线性律的战斗过程
    predict(R0, B0, b_l, a_l, mode)
    for t in np.arange(0, T, dt):
        LinearLaw(R, B, b_l, a_l, t)
        if R[-1] < 1e-6 or B[-1] < 1e-6:
            break
elif mode == "ModernizedLanchesterModel":
    # 初始化参数
    f_r = 0.6                               # 红方的伪装能力系数
    s_r = 0.6                               # 红方的侦察能力
    f_b = 0.2                               # 蓝方的伪装能力系数
    s_b = 0.2                               # 蓝方的侦察能力
    epsilon_r = 4                           # 红方信息作战能力系数
    epsilon_b = 4                           # 蓝方信息作战能力系数
    for t in np.arange(0, T, dt):
        MoLanMdl(R, B, b_s, a_s, b_l, a_l, f_r, s_r, f_b, s_b, epsilon_r, epsilon_b, t)
        if R[-1] < 1e-6 or B[-1] < 1e-6:
            break

这里的三个if()判断就是用来判断执行何种模式的Lanchester方程仿真验证的。

总结

这篇论文没有给出如何将连续域的Lanchester方程转换为离散域的差分方程，得研究一下如何将微分方程转换成差分方程的方法。
不过，微分方程转换成离散方程再用代码来进行仿真验证，就不用费心费力地去算微分方程的解了，值得学习一下思路。

雷烈

（1）间瞄火力的Lanchester方程

公式

参数说明

Python 代码实现

（2）平方律的Lanchester方程

公式

参数说明

Python 代码实现

（3）信息对抗因素的Lanchester方程

公式

参数说明

Python 代码实现

Python 代码

源码如下

代码解释

（1）模式选择

（2）进行仿真

总结